Порядок выполнения работы:

Из технической механики известно, что для центрального кривошипно-шатунного механизма (у которого ось цилиндра пересекает ось коленчатого вала) ускорение поршня «а» определяется приближенным выражением а = Rω²(cosφ + λcos2φ), где R – радиус кривошипа, м; ω = Пn/30 – угловая скорость, рад/с (n - расчетная частота вращения, об/мин); λ – R/L (L – длина шатуна, м); φ – угол поворота кривошипа, отсчитываемой от ВМТ. В этом случае выражение для сил инерции поступательно движущихся частей примет окончательный вид:

Ри = - М R ω²(cosφ + λcos2φ) (16.1)

Из этого уравнения следует, что силы инерции поступательно движущихся частей изменяются как по величине, так и по направлению в зависимости от угла φ, причем эти изменения будут периодическими.

Известно, что сила инерции достигает наибольшего значения там, где скорость становится равной нулю и меняет свой знак. Такими положениями для кривошипно-шатунного механизма должны быть мертвые точки. В ВМТ при φ = 0º выражение (16.1) принимает вид:

Ри = - М R ω²(1 + λ) (16.2)

в НМТ при φ = 180º Ри = - М R ω²(-1 + λ) = - М R ω²(1 - λ) (16.3)

Как видно в ВМТ силы инерции подвижных частей имеют отрицательное и наибольшее абсолютное значение, а в НМТ они положительны и принимают несколько меньшее значение, если иметь в виду, что λ = 1/3,5 - 1/5.

Кроме поступательно движущихся частей в двигателе есть вращательно движущиеся части, к которым относится неуравновешенная часть кривошипа и вращающаяся часть шатуна (условно ~ 60% Gш). Массы этих частей считаются сосредоточенными на оси шейки кривошипа. Так как центростремительное ускорение в этой точке а_ц = R ω², то сила инерции вращающихся частей Рц = -М R ω², где Мц – масса вращающихся частей, кг. Знак «минус» указывает, что эта сила направлена от центра вращения по радиусу кривошипа.

Таким образом, в кривошипно-шатунном механизме работающего двигателя в любой промежуток времени действуют силы от давления газов, силы тяжести и силы инерции поступательно движущихся частей, алгебраическая сумма которых выразится равнодействующей Рg, называемой движущей силой.

Рg = ±Рч ± Рв ± Ри (16.4)

Все эти силы, в том числе и движущая, считаются положительными (знак «+»), если они способствуют движению поршня и наоборот.

Движущая сила действует по оси цилиндра и приложена в центре головного соединения точке А (рис.16.1).

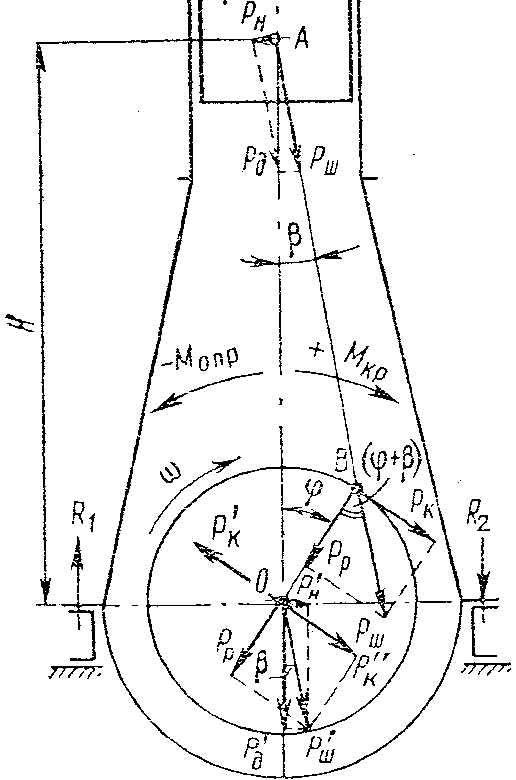
Рис.16.1 Схема сил, действующих в кривошипно-шатунном механизме

Разложим равнодействующую Рg по правилам механики на две составляющие: Рш, направленную на оси шатуна, и Рн, направленную перпендикулярно оси цилиндра. Условимся, что угол поворота кривошипа имеет некоторое мгновенное значение φ, а между осями цилиндра и шатуна образуется угол β. Сила Рн = Рц tgβ, которая называется нормально силой, прижимая поршень поочередно к противоположным стенкам цилиндра, вызывает износ цилиндропоршневой группы в этой плоскости (износ на эллипс).

В крейцкопфных двигателях сила Рн имеет большое значение и передается ползунам крейцкопфа на параллели, что облегчает условия работы цилиндропоршневой группы, именно этими обстоятельствами объясняется крейцкопфное исполнение малооборотных двухтактных двигателей.

Сила, действующая по оси шатуна Рш = Рg/cosβ, стремится сжать стержень шатуна. Перенося эту силу на ось шейки кривошипа в точку В, разложим ее по двум направлениям – по радиусу кривошипа и по касательной к окружности, описываемой центром шейки вала. Радиальная сила Рр определяется выражением:

Рр = Рш cos (φ + β) = Pg cos(φ + β)/cos β

Касательная (тангенциальная) сила Рк

Рк = Рш sin (φ + β) = Pg sin(φ + β)/cos β (16.5)

Перенесем радиальную силу Рр по направлению ее действия в центр коленчатого вала «О» и приложим одновременно к центру вала две взаимно противоположные и равные силы Рк’ и Рк”, параллельные и равные, в свою очередь, касательной силе Рк. Силы Рк’ и Рк” на плече R образуют пару сил, момент которой называется крутящим моментом. Этот момент приводит во вращение коленчатый вал и в общем случае Мкр = Рк*R. Из-за периодического изменения касательной силы величина крутящего момента также будет переменной. Дальнейшее сложение сил Рк” и Рр, приложенных к центру вала, дает результирующую силу Рш’, которая прижимает вал к вкладышам рамовых подшипников.

Раскладывая силу Рш’ на составляющие Рн и Pg’ и, имея в виду, что угол между силами Рш’ и Pg’ равен β, получим, что Рн’ = Рн, а Pg’ = Рg. Из выражения (16.4) следует, что в состав силы Рg входит сила от давления газов Рч, которая имеет абсолютно наибольшее значение по отношению к другим составляющим и поэтому без большой погрешности можно принять Рg ≈ Рч. В этом случае силы Рg’ и Рч’, действующие по оси цилиндра, условно равные и направленные в противоположные стороны, будут вызывать растягивающие нагрузки в деталях остова, а при наличии анкерных связей растягивать их.

Равные по величине и противоположные по направлению силы Рн и Рн’ образуют пару сил с плечом Н. создаваемый ими момент называется опрокидывающим, так как он стремится повернуть двигатель вокруг продольной оси в сторону, противоположную вращению коленчатого вала. Опрокидывающий момент численно равен крутящему, но направлен в противоположную сторону Мопр = - Мкр. Опрокидывающий момент передается опорам фундамента, вызывая в них реакции R₁ и R

Для определения касательной силы при любом значении угла поворота кривошипа в пределах цикла, то есть от 0 до 720º для четырехтактных и от 0 до 360º для двухтактных двигателей, необходимо построить диаграмму касательных сил, которая наглядно покажет характер и закономерность изменения касательной силы за цикл.

Касательная сила представляет собой произведение движущей силы на тригонометрическую функцию углов φ и β. Следовательно, для построения кривой касательных усилий предварительно необходимо построить диаграмму движущих сил. Известно, что движущая сила равна алгебраической сумме сил от давления газа, силы тяжести поступательно движущихся частей и их сил инерции. Подобное суммирование удобно провести графически, для чего следует все три составляющие силы привести к единице измерения давления газов, Па. В формуле сил инерции эти достигается заменой всей массы М движущихся частей массой «m», приходящейся на единицу площади поршня m = M/F, где F – площадь днища поршня, м².

Ри = - m R ω²(cosφ + λcos2φ)

Силы тяжести поступательно движущихся частей и давление газов, отнесенные к единице площади поршня, обозначим соответственно Рв и Рч.

Давление газов на поршень в зависимости от его положения определяется по индикаторной диаграмме расчетного цикла.

П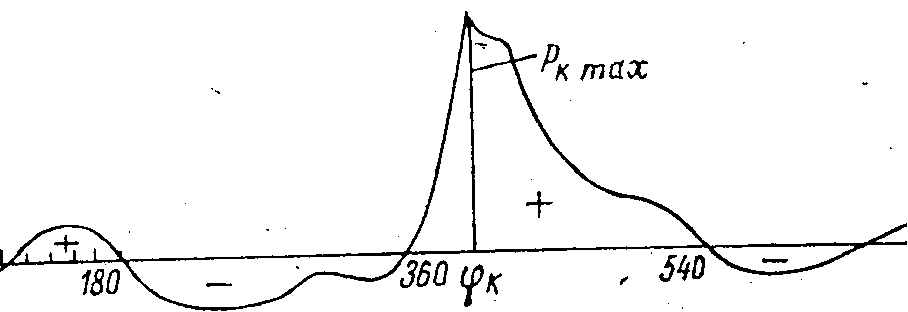 остроим диаграмму касательных усилий для одного цилиндра (рис.16.5).

Рис.16.5 Диаграмма касательных усилий для одного цилиндра

Масштабы остаются прежними. Умножив значение ординат Pg на отношение (sin(φ + β))/cos β, которое определяется из специальных таблиц (для принятого значения λ), получим ординаты кривой касательных сил Рк. Положительные значения касательных сил откладывают вверх от оси абсцисс, отрицательные - вниз. Касательная сила равна нулю в точках, соответствующих наклону кривошипа 0, 180, 360, 540, 720º, так как в этих точках значение функции sin(φ + β)/cosβ = 0. Касательная сила равна нулю также в точках пересечения кривых сил давления газов и сил инерции. На промежуточных участках, где направление движущей силы совпадает с направлением движения поршня, касательная сила имеет знак «плюс», а на остальных участках – знак «минус».

Соединив концы ординат плавной кривой, получим диаграмму изменения касательных сил для одного рабочего цилиндра за полный цикл.

За весь период от 0 до 720º, соответствующий одному циклу, касательная сила многократно меняет направление (знак) на обратное и один раз достигает максимального положительного значения Рк_max. В дизелях Рк_max обычно наблюдается через 20-30º за ВМТ на ходе расширения (угол на рис.16.5).

Изменение касательного усилия многоцилиндрового двигателя представляется суммарной диаграммой касательных усилий (рис.16.6), которая для всех цилиндров может быть построена путем суммирования ординат кривых касательных усилий от всех цилиндров, сдвинутых по отношению один к другому на угол заклинивания кривошипов φ_о, который из условия равномерности вращения коленчатого вала принимают равным φ_о = 360/kz.

Н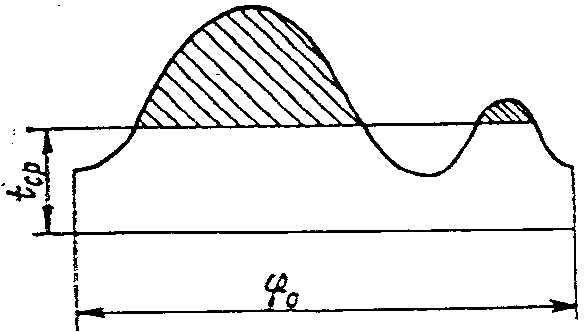 а рис.16.6 суммарная кривая построена для одного участка φ_о. На остальных участках она будет повторяться. Если построение диаграммы отнести к четырехтактному шестицилиндровому двигателю (φ_о = 120º), то полная суммарная диаграмма будет иметь шесть таких участков за цикл.

Рис.16.6 Суммарная диаграмма касательных усилий

Суммарную диаграмму касательных усилий можно превратить в диаграмму вращающихся моментов, если по оси ординат откладывать значение вращающихся моментов (Мвр = Σр_кR) для различных значений φ. В этом случае площадь диаграммы, ограниченная кривой, будет изображать работу, которую совершает двигатель за один цикл, так как произведение Мвр φ в общем случае представляет собой работу при вращательном движении.

При разных углах кривошипа полезный крутящий момент двигателя будет различным, а момент сопротивления, который должен преодолевать двигатель, обычно постоянен. Усилие, создающее этот момент, равно некоторому среднему касательному усилию t_ср.

Для определения ординаты среднего касательного усилия необходимо спланировать ΣF площадь, ограниченную линией абсцисс и суммарной кривой касательных усилий, разделив ее на длину l диаграммы:

t_cp = ΣF / l*a

где a – масштаб сил, МПа;

l – длина диаграммы, м;

F – площадь диаграммы, м².

В принятом масштабе ординату t_cp наносят на суммарную диаграмму касательных усилий и проводят линию, параллельную оси абсцисс, которую называют линией среднего сопротивления. Определить ординату t_cp можно также в зависимости от среднего индикаторного давления

t_cp = Pi k z / П

Если условно рассматривать суммарную диаграмму касательных усилий как диаграмму вращающихся моментов, то площадки, расположенные выше средней линии сопротивлений (на рис.16.6 заштрихованы), будут пропорциональны избыточной работе движущейся силы, поглощаемой маховиком и вращающимися массами подвижных частей двигателя. Площадки, расположенные ниже линии t_cp, будут пропорциональны работе, отдаваемой движущимися частями и маховиком в период, когда Рк меньше своего среднего значения.

Содержание отчета:

1. Тема и цель практического занятия.

2. Материальное обеспечение.

3. Отчет о проделанной работе.

Заключительный контроль:

1. Как изображаются положительные и отрицательные значения касательных сил?

2. В каких точках диаграммы касательная сила равна нулю?

3. При каких градусах касательная сила имеет максимальное значение?

4. Как выглядит суммарная кривая касательных сил?

5. Определение t_cp на диаграмме.

6. Определение избыточной работы движущихся сил.

7. Что отображают площадки, расположенные ниже t_cp? Формула ускорения поршня и от каких величин она зависит?

8. Сила инерции поступательно движущихся частей.

9. Сила инерции вращающихся частей.

10. Движущая сила, ее составляющие.

11. Действие радиальной силы.

12. Действие касательной силы.

13. От каких сил и плеча зависит опрокидывающий момент?

Литература:

1. Методические указания к выполнению лабораторных и практических работ по дисциплине «Судовые энергетические установки и их эксплуатация», 1985.

2. Миклос А.Г., Чернявская Н.Г., Червяков С.П. Судовые двигатели внутреннего сгорания, 1986.