4. Ряд распределения дискретной случайной величины

随机变量及其分布

4.1. Основы теории дискретных случайных величин

基本随机变量的理论

Закон распределения дискретной случайной величины Х имеет форму ряда распределения. Это таблица, связывающая все возможные значения случайной величины и вероятности, с которыми эти значения реализуются.随机变量的分布规律具有分布形式公式。下面表格，包括所有变量的数值与相应概率。

Х			. . .
Р			. . .

Вероятности реализации событий связаны соотношением所有这些概率合起来是1.

(4.1)

Графическое изображение ряда распределения называется полигоном распределения.图像绘制分布排列叫分布轨迹。

4.2. Пример решения типовых заданий по теме «Ряд распределения дискретной случайной величины» 例题详解

Задание № 4. Вариант 1. Коля, Петя и Сережа готовятся к экзамену по статистике. Коля может получить пятерку с вероятностью 90%, Петя – 70%, а Сережа – 20%. Построить ряд распределения и полигон числа пятерок, которые друзья могут получить на экзамене по статистике.

Коля, Петя и Сережа三人准备统计考试，Коля可以获得5分的概率是90%, Петя 是70%， Сережа是20%。建立统计考试5分的分布规律与图像。

Решение. Прежде всего, определим форму ряда распределения случайной величины Х – числа пятерок, которые трое друзей могут получить на экзамене по статистике. Действительно, на троих они могут не получить ни одной пятерки, получить 1, 2 или 3 пятерки. Значит, ряд распределения в общем виде таков:首先决定三人获得5分的随机变量分布规律公式，当然三人可能获得不知一个，可能1个，2个，或者3个5分。

Х	0	1	2	3
Р

Осталось найти значения вероятностей .

Обозначим вероятности получения пятерки Колей = 0,9, Петей = 0,7, Сережей = 0,2. Соответственно, вероятность не получить пятерку для Коли = 1 – 0,9 = 0,1, для Пети = 1 – 0,7 = 0,3, для Сережи = 1 – 0,2 = 0,8.

Тогда вероятность не получить ни одной пятерки для трех друзей будет 三人1个5分都没有的概率

.

Событие «Получить 1 пятерку на троих» означает, что пятерку получит или Коля, или Петя, или Сережа, а остальные двое пятерок не получат. Вероятность этого события三人获得一个5分，意味着其中一人5分，另外两人没有5分，这个概率是

= 0,216 + 0,056 + 0,006 = 0,278.

Аналогично вычисляется вероятность получения двух пятерок на троих

Вероятность получения пятерок всеми 3 друзьями равна

.

Найденные значения вероятностей позволяют завершить составление ряда распределения случайной величины Х, который принимает вид

Х	0	1	2	3
Р	0,024	0,278	0,572	0,126

Очевидно, что 0,024 + 0,278 + + 0,572 + 0,126 = 1, т.е. выполняется соотношение (4.1) и построенный ряд распределения отвечает требованиям нормировки.

Наиболее вероятным оказалось событие «Получить 2 пятерки на троих». Действительно, исходные значения вероятностей свидетельствуют в пользу того, что Петя и Коля, скорее всего, получат пятерки по статистике, а Сережа – нет. Как правило, результат математических вычислений в теории вероятностей подтверждает соображения житейской логики.

Графический образ построенного ряда распределения – полигон.建立图像。 Для построения полигона по оси Х отложим в выбранном масштабе значения случайной величины: 0, 1, 2 и 3. На оси У найдем в другом масштабе соответствующие этим значениям вероятности: 0,024, 0,278, 0,572 и 0,126. Это будут соответственно абсциссы и ординаты узловых точек полигона. Построим эти узловые точки по заданным координатам. Соединив их отрезками прямых линий, получим требуемый чертеж полигона (рис. 4.1).

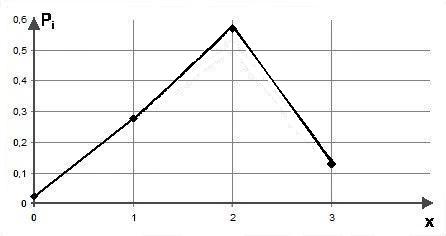
Рис. 4.1. Полигон числа пятерок, полученных друзьями на экзамене по статистике

Задание № 4. Вариант 2. Компьютерный класс № 1 бывает занят в день 4 или 6 часов в зависимости от четной или нечетной учебной недели. Компьютерный класс № 2 используется для тестирования и бывает занят 3 часа в день в 90% случаев или 5 часов – в 10% случаев. Построить ряд распределения и полигон общего числа часов дневной занятости компьютерных классов. 计算机1号教室可能在单双周每天使用4个课时或者6个课时。计算机2号教室90%的时间每天使用3个课时，或者10%的时间每天使用5个课时。建立计算机教室使用随机变量分布规律和图像。

Решение. Пусть случайная величина Х – число часов в день, когда заняты оба компьютерных класса. Для построения ряда распределения Х сначала составим ряды распределения величин и - числа часов занятости компьютерных классов № 1 и № 2 по отдельности.设随机变量X为每天两间教室的课时数量，先分别建立不同教师的随机变量分布规律。

	4	6			5	7
Р	0,5	0,5		Р	0,9	0,1

Случайная величина Х может принимать значения, равные возможным суммам значений величин и . Ряд распределения Х имеет вид

随机变量X可以取不同的课时总数

Х	9	11	13
Р

Найдет значения вероятностей , , . Значение Х = 9 случайная величина принимает, если компьютерный класс № 1 работает 4 часа, а класс № 2 – 5 часов:

.

Значение Х = 11 случайная величина принимает, если компьютерный класс № 1 работает 4 часа, а класс № 2 – 7 часов или компьютерный класс № 1 работает 6 часов, а класс № 2 – 5 часов:

.

Значение Х = 13 случайная величина принимает, если компьютерный класс № 1 работает 6 часов, а класс № 2 – 7 часов:

.

Ряд распределения случайной величины Х можно записать в виде

Х	9	11	13
Р	0,45	0,5	0,05

Очевидно, что 0,45 + 0,5 + + 0,05 = 1, и для построенного ряда выполнено соотношение нормировки (4.1)..

Полигон распределения строится аналогично варианту 1 (рис. 4.2).

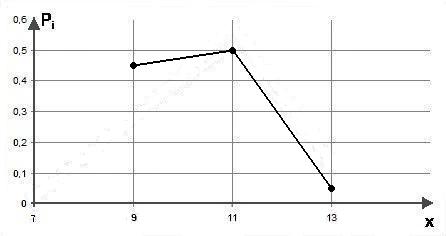
Рис. 4.2. Полигон числа часов дневной загрузки двух компьютерных классов