
- •Оглавление
- •1. Выбор на основе классического определения вероятности
- •1. Основы выбора на базе классического определения вероятности
- •1.2. Решение типового задания по теме «Выбор на основе классического определения вероятности» 解题方法
- •1.3. Задания по теме «Выбор на основе классического определения вероятности» 习题
- •Сумма и произведение событий
- •2.1. Основы алгебры событий 基本事件代数
- •2.2. Решение типового задания по теме «Сумма и произведение событий» 例题解答
- •2.3. Задания по теме «Сумма и произведение событий»习题
- •Формула полной вероятности и формула байеса
- •3.1. Основы экспертного оценивания 基本评估
- •Пример решения типового задания по теме «Формула полной вероятности и формула Байеса»例题解答
- •3.3. Задания по теме «Формула полной вероятности и формула Байеса» 习题
- •Ряд распределения дискретной случайной величины
- •4.1. Основы теории дискретных случайных величин
- •4.2. Пример решения типовых заданий по теме «Ряд распределения дискретной случайной величины» 例题详解
- •4.3. Задания по теме «Ряд распределения дискретной случайной величины»习题
- •Числовые характеристики дискретной случайной величины
- •5.1. Основы теории числовых характеристик дискретной случайной величины 随机变量数字特征基本理论
- •5.2. Пример решения типового задания по теме «Числовые характеристики дискретной случайной величины»
- •5.3. Задания по теме «Числовые характеристики дискретной случайной величины»习题
- •Варианты задания
- •Биномиальное распределение 二项分布、伯努利实验 (схема бернулли)
- •6.1. Основы теории биномиального распределения 二项分布基本理论
- •6.2. Пример решения типового задания по теме «Биномиальное распределение»例题详解
- •6.3. Задания по теме «Биномиальное распределение» 习题
- •7. Распределение пуассона (закон редких событий)泊松分布
- •7.1. Основы теории распределения Пуассона
- •7.2. Пример решения типового задания по теме «Распределение Пуассона»例题详解
- •7.3. Задания по теме «Распределение Пуассона» 习题
- •8. Равномерное распределение
- •8.1. Основы теории равномерного распределения均匀分布的基础理论
- •8.2. Пример решения типового задания по теме «Равномерное распределение» 例题详解
- •8.3. Задания по теме «Равномерное распределение» 习题
- •Варианты задания
- •9. Локальная и интегральная теоремы лапласа
- •9.1. Основы применения теорем Лапласа для приближенного вычисления вероятностей событий при независимых испытаниях独立实验中使用拉普拉斯定理计算事件概率
- •9.2. Пример решения типового задания по теме «Локальная и интегральная теоремы Лапласа» 例题详解
- •9.3. Задания по теме «Локальная и интегральные теоремы Лапласа»
- •10. Вариационный и статистический ряды
- •10.1. Основы выборочного метода 基本样本方法
- •10.2. Пример решения типового задания по теме «Вариационный и статистический ряды» 例题详解
- •10.3. Задания по теме «Вариационный и статистический ряды»习题
- •Варианты задания
- •11. Группированный статистический ряд
- •11.1. Основы группировки статистических данных
- •11.2. Пример решения типового задания по теме «Группированный статистический ряд»
- •11.3. Задания по теме «Группированный статистический ряд»
- •Варианты задания
- •12. Точечные оценки выборочных числовых характеристик 点估计
- •12.1. Основы точечного оценивания
- •12.2. Пример решения типового задания по теме «Точечные оценки выборочных числовых характеристик»
- •12.3. Задания по теме «Точечные оценки выборочных числовых характеристик»
- •Варианты задания
- •13. Точность и надежность оценки вероятности 估计概率的准确性与可靠性 (формула муавра-лапласа)
- •13.1. Основы интервального оценивания вероятности 区间估计
- •13.2. Пример решения типового задания по теме «Точность и надежность оценки вероятности»
- •13.3. Задания по теме «Точность и надежность оценки вероятности» 习题
- •14. Проверка гипотез методом доверительных интервалов
- •14.1. Основы проверки гипотез методом доверительных интервалов
- •14.2. Пример решения типового задания по теме «Проверка гипотез методом доверительных интервалов»例题详解
- •14.3. Задания по теме «Проверка гипотез методом доверительных интервалов»习题
- •15. Критерий пирсона
- •15.1. Основы проверки гипотезы о нормальном распределении
- •15.2. Пример решения типового задания по теме «Критерий Пирсона»
- •15.3. Задания по теме «Критерий Пирсона»
- •Варианты задания
- •16. Корреляционный анализ 相关分析
- •16.1. Основы корреляционного анализа
- •Степени корреляции
- •16.2. Пример решения типового задания по теме «Корреляционный анализ»
- •16.3. Задания по теме «Корреляционный анализ»
- •Варианты задания
- •17. Корреляционный анализ при дихотомическОм оценивании
- •17.1. Основы применения корреляционного анализа при дихотомическом оценивании
- •Степени тесноты связи при дихотомическом оценивании
- •17.2. Пример решения типового задания по теме «Корреляционный анализ при дихотомическом оценивании»
- •17.3. Задания по теме «Корреляционный анализ при дихотомическом оценивании»
- •Варианты задания
- •18. Регрессионный анализ 回归分析
- •18.1. Основы регрессионного анализа
- •18.2. Пример решения типового задания по теме «Регрессионный анализ»
- •18.3. Задания по теме «Регрессионный анализ»
- •Варианты задания
- •Приложения
- •Функция гаусса
- •Функция лапласа
- •Распределение χ2
Формула полной вероятности и формула байеса
全概率公式和贝叶斯公式
3.1. Основы экспертного оценивания 基本评估
Пусть
относительно наступления события А
можно выдвинуть n
попарно несовместных гипотез
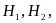 .
. .
.
. .
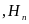 ,
априорные вероятности которых известны:
,
априорные вероятности которых известны:
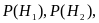 . . . ,
. . . ,
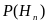 .
Обычно предполагают, что гипотезы
образуют полную группу, т.е. выполняется
условие让事件A相对抽出n对不相容的假设为
.
Обычно предполагают, что гипотезы
образуют полную группу, т.е. выполняется
условие让事件A相对抽出n对不相容的假设为![]() .
. .
.
. .
![]() ,先期已知的概率为
,先期已知的概率为![]() . . . ,
. . . ,
![]() ,一般假定组成完整分组,满足下面条件:
,一般假定组成完整分组,满足下面条件:
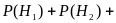 .
. .
.
. .
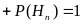 .
(3.1)
.
(3.1)
Событие
А
может
наступить только вместе с одной из
гипотез, причем известны условные
вероятности наступления этого события
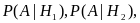 . . . ,
. . . ,
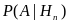 .
Тогда вероятность наступления события
А
может быть вычислена по формуле полной
вероятности:事件A发生出现一种假定的概率为
.
Тогда вероятность наступления события
А
может быть вычислена по формуле полной
вероятности:事件A发生出现一种假定的概率为![]() . . . ,
. . . ,
![]() ,那么发生事件A的全概率可根据公式得出:
,那么发生事件A的全概率可根据公式得出:
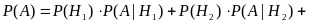 .
. .
.
. .
+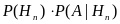 .
(3.2)
.
(3.2)
Пусть событие А произошло. Тогда можно переоценить вероятности гипотез, которые приводят к появлению этого события. Апостериорные вероятности гипотез вычисляются по формуле Байеса:让事件A发生,那么可以假定发生的概率。实际发生的概率可以根据贝叶斯公式求得:
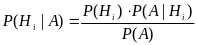 ,
,
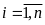 ,
(3.3)
,
(3.3)
где
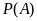 вычисляется по формуле полной вероятности
(3.2).
вычисляется по формуле полной вероятности
(3.2).
Если
событие А не
произошло, это означает, что произошло
противоположное событие
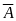 .
Его вероятность
.
Его вероятность
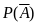 находится по формуле полной вероятности,
аналогичной (3.2). При этом вероятности
гипотез не меняются, а условные вероятности
наступления события
находятся по формуле вероятности
противоположного события:
如果事件A没有发生,这意味着发生对立事件A,它的概率可根据全概率公式得到。这个情况下假定不发生变化,那么事件A发生的条件可根据对立事件公式得出:
находится по формуле полной вероятности,
аналогичной (3.2). При этом вероятности
гипотез не меняются, а условные вероятности
наступления события
находятся по формуле вероятности
противоположного события:
如果事件A没有发生,这意味着发生对立事件A,它的概率可根据全概率公式得到。这个情况下假定不发生变化,那么事件A发生的条件可根据对立事件公式得出:
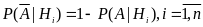 .
.
Апостериорные
вероятности гипотез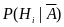 находятся
по формуле Байеса, аналогичной (3.3).
находятся
по формуле Байеса, аналогичной (3.3).
Пример решения типового задания по теме «Формула полной вероятности и формула Байеса»例题解答
Задание № 3. На курсе 120 студентов обучаются по направлению подготовки «Регионоведение», 70 – «Реклама». Абсолютная успеваемость студентов – регионоведов составляет 85%, студентов-рекламщиков – 55%. 《区域学》有120名学生,《广告学》有70名。顺利结束学业的学生《区域学》85%,《广告学》55%。
1. Какова вероятность, что случайно выбранный студент данного курса – успевающий?随机抽取到顺利结业学生的概率
2. Найти вероятность, что этот студент обучается по направлению подготовки «Реклама». 求抽取到《广告学》学生的概率
Решение. Событие А – выбранный студент успевающий. Выбранный студент может обучаться по одному из двух направлений подготовки, т.е. рассматриваем две гипотезы:事件A-顺利结业,所选学生可以学习其中一个方向,那么分析两种情况
 – студент
обучается по направлению
«Регионоведение»,学生学习《区域学》
– студент
обучается по направлению
«Регионоведение»,学生学习《区域学》
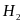 – студент
обучается по направлению «Реклама».学生学习《广告学》
– студент
обучается по направлению «Реклама».学生学习《广告学》
Тогда вероятности гипотез равны процентным долям студентов этих направлений относительно общего числа студентов курса. На курсе учится 120 + 70 = 190 студентов. Поэтому вероятности гипотез можно вычислить так:那么概率等于学习各专业方向除以总人数。总人数味190人,所以:
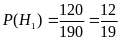 ,
,
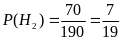 .
.
Заметим, что выполняется условие (3.1), что делает возможным впоследствии применять формулу Байеса. Действительно如果满足(3.1)的条件,就可以使用贝叶斯公式。
 .
.
Вероятность того, что студент-регионовед успевает равна 85%, т.е.
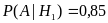 .
Аналогично для студента-рекламщика
.
Аналогично для студента-рекламщика
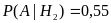 .
.
Тогда вероятность того, что выбранный студент успевающий, можно найти по формуле полной вероятности (3.2):所选顺利结业学生的概率,可以用全概率公式求得:
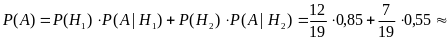
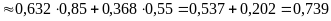 .
.
Значит, абсолютная успеваемость студентов курса составляет примерно 74%. 也就是说整个年级学生合格率为74%.
Найдем вероятность того, что выбранный случайным образом студент обучается по направлению «Реклама». Применяем формулу Байеса (3.3):求随机抽取的学习《区域学》的学生概率,可通过贝叶斯公式求得:
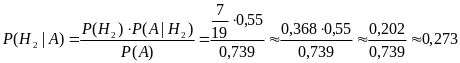 .
.
Вероятность составляет примерно 27%. Это немного, и вполне укладывается в представления житейской логики – действительно, и студентов-рекламщиков на курсе меньше и доля успевающих среди них ниже, чем среди регионоведов.概率大约是27%,这个概率不大,也是遵循逻辑可信的,那么年级中广告学学生更少,并且顺利结业的学生也更少。
