18. Регрессионный анализ 回归分析
18.1. Основы регрессионного анализа
Для того чтобы оценить адекватность и точность модели зависимости случайных величин в форме линейной корреляционной связи используют регрессионный анализ. 线性回归是利用数理统计中的回归分析来确定两种或两种以上变量相互依赖的定量关系的一种统计分析。
Пусть дана двумерная выборка
Х |
|
|
..... |
|
У |
|
|
..... |
|
По формулам (16.1)-(16.8) найдем числовые характеристики выборки: выборочные средние , выборочные отклонения , выборочный коэффициент корреляции . Уравнения прямых регрессий имеют вид:
– регрессия
У
на Х,
(18.1)
– регрессия
Х
на У.
(18.2)
Обе
линии прямых регрессий изображаются
на графике вместе с облаком точек. Об
адекватности построенной линейной
корреляционной модели можно судить по
тому, насколько хорошо обе линии
регрессий аппроксимируют облако точек.
О степени корреляционной связи
свидетельствует определенная (угловая)
близость линий регрессии. Чем теснее
связь, тем меньше угол между линиями
регрессий. При отсутствии корреляционной
связи между величинами Х
и У
(
=
0) прямые регрессий параллельны осям
координат (
),
облако точек носит хаотический характер.
18.2. Пример решения типового задания по теме «Регрессионный анализ»
Задание № 18. Дана двумерная выборка. Написать уравнения прямых регрессий. На графике изобразить облако точек и линии прямых регрессий. Сделать предварительный вывод об адекватности линейной корреляционной модели.
-
Х
1
2
3
4
5
6
У
10
10
6
6
2
1
Решение. По формулам (16.1) – (16.8) найдем числовые характеристики выборки.
;
;
;
;
;
;
;
.
Тогда запишем уравнения прямых регрессий:
– регрессия
У
на Х,
– регрессия
Х
на У.
После преобразований получаем
– регрессия
У
на Х,
– регрессия
Х
на У.
Облако точек и линии прямых регрессий построены на рис. 18.1. Видно, что линейная корреляционная модель адекватна, поскольку обе линии регрессий хорошо аппроксимируют облако точек. Кроме того, прямые регрессий близки, что указывает на сильную корреляционную связь между величинами Х и У.
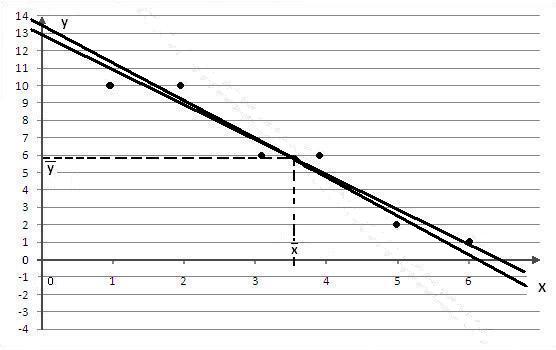
Рис. 18.1. Облако точек и линии прямых регрессий
18.3. Задания по теме «Регрессионный анализ»
Текст задания. Дана двумерная выборка. Написать уравнения прямых регрессий. На графике изобразить облако точек и линии прямых регрессий. Сделать предварительный вывод об адекватности линейной корреляционной модели.
Таблица 18.1