10. Вариационный и статистический ряды

变更与统计序列

10.1. Основы выборочного метода 基本样本方法

Пусть дана выборка объемом n. 设给定样本容量为n，

. . . . .

Вариационный ряд – это упорядоченная по возрастанию последовательность всех элементов выборки (включая повторяющие элементы):变更序列是所有元素按增大的顺序选择，包括重复的元素。

. . . . .

Крайние элементы вариационного ряда называются экстремальными:边缘元素在变更序列称为极限。

, . (10.1)

Медианой называется средний элемент вариационного ряда:变更序列中的平均值元素称为中位数

m ed = (10.2)

Квартилями называются элементы вариационного ряда, отстоящие от концов на ¼. Для того, что найти квартили сначала определяют значение индекса i:四分位数是变更序列的元素的四分之一，得出四分位数需要先确认指数i

i = (10.3)

где [t] означает целую часть числа. Например, [4,7] = 4, [0,2] = 0, [5,9] = 5.

Тогда можно найти нижнюю квартиль 第一四分位数

, (10.4)

и верхнюю квартиль第三四分位数

. (10.5)

Графически основные параметры вариационного ряда изображаются с помощью ящика с усами или бокс-флота. 建立的图像称为箱线图。

Статистический ряд – это последовательность различных элементов вариационного ряда с указанием числа повторений (частот) . Обычно эти значения дополняются относительными частотами

: (10.6)

			. . . . .
			. . . . .
			. . . . .

Графическое изображение статистического ряда – полигон, построение которого аналогично описанному в разделах 4 и 5 с заменой вероятностей на частоты или на относительные частоты , откладываемые по оси У.

Выборочная функция распределения строится по алгоритму, описанному в разделе 5 с заменой вероятностей на относительные частоты.

10.2. Пример решения типового задания по теме «Вариационный и статистический ряды» 例题详解

Задание № 10. Дана выборка. Составить вариационный и статистический ряды. Найти экстремальные элементы, медиану, квартили. Построить ящик с усами, полигон, выборочную функцию распределения. Сделать предварительный вывод о характере распределения значений выборки.给定选择，组建变更与统计序列。得出极限元素，中位数，四分位数。建立图像箱线图，点场，分布函数。并得出大致分布性质总结。

5	1	12	5	21	21	5	5	12
5	12	1	1	5	5	27	21
27	32	5	32	1	12	5	1

Решение. Объем выборки n = 25. Построим вариационный ряд – упорядочим выборку по возрастанию.

1	1	1	1	1	5	5	5	5
5	5	5	5	5	12	12	12	12
21	21	21	27	27	32	32

Экстремальные элементы находятся по формулам (10.1):

, .

Поскольку объем выборки n = 25, то для нахождения медианы пользуемся первой из формул (10.2) – для выборки нечетного объема:

.

Для нахождения квартилей определим значение индекса i. Поскольку n = 25 не делится нацело на 4, то пользуемся второй из формул (10.3):

.

Тогда нижнюю и верхнюю квартили находим по формулам (10.4) и (10.5):

,

.

На основании полученных данных можно построить ящик с усами (рис. 10.1).

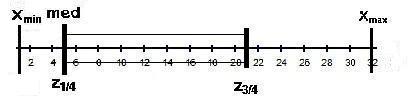
Рис. 10.1. Ящик с усами (бокс-флот)

Можно провести предварительный анализ выборки уже на основе построенного ящика с усами. Видно, что значения случайной величины смещены в левую часть занимаемого ей на оси интервала. Во-первых, медиана, равная 5, значительно смещена влево от геометрической середины интервала [1, 32], равной 15,5. Во-вторых, медиана совпадает с нижней квартилью, указывая на преимущественное смещение среднего по объему значения в сторону первой четверти объема значений. В-третьих, половина значений случайной величины, заключенная между квартилями, также располагается преимущественно слева от геометрической середины интервала распределения. Таким образом, можно охарактеризовать представленное распределение как асимметричное со смещением влево.

Построим статистический ряд, ставя в соответствие значениям случайной величины не только частоты (количество повторений), но и относительные частоты, вычисленные по формуле (10.6).

	1	5	12	21	27	32
	5	9	4	3	2	2
	5/25	9/25	4/25	3/25	2/25	2/25

График статистического ряда – полигон, изображен на рис. 10.2.

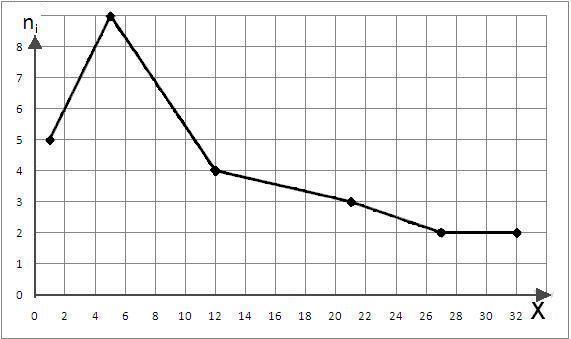
Рис. 10.2. Полигон

Выборочную функцию распределения строим, используя правило, аналогичное (5.5):

,

,

,

.

Таблица значений выборочной функции распределения имеет вид

Х
	0	0,2	0,56	072	0,84	0,92	1

График выборочной функции распределения приведен на рис. 10.3.

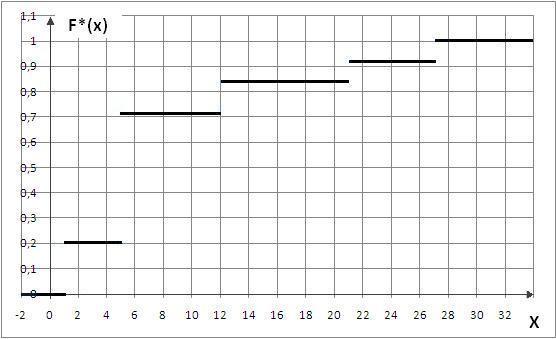
Рис. 10.3. Выборочная функция распределения样本函数分布