9. Локальная и интегральная теоремы лапласа

9.1. Основы применения теорем Лапласа для приближенного вычисления вероятностей событий при независимых испытаниях独立实验中使用拉普拉斯定理计算事件概率

Если в схеме независимых испытаний Бернулли число опытов велико (десятки, сотни), то для подсчета вероятностей числа успехов можно пользоваться приближенными формулами, следующими из интегральной и локальной теорем Лапласа. То есть фактически дискретная случайная величина, распределенная по биномиальному закону, заменяется дискретным аналогом непрерывной случайной величины, распределенной по нормальному закону.

设在独立实验n序列中，事件A在各次实验中发生一种可能的概率为p，不发生的概率为q=1-p, 随机变量为X- 在n次试验中发生事件A的数量。

Пусть производится n независимых опытов. Событие А может появиться в одном опыте с вероятностью р, либо не появиться с вероятностью q = 1 – р. Случайная величина Х – число появлений события А в серии из n опытов.

Вероятность того, что случайная величина принимает определенное значение Х = m, можно найти с использованием локальной теоремы Лапласа:

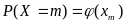, (9.1)

где – функция Гаусса, значения которой сведены в таблицу в Приложении 1. Значение аргумента функции Гаусса вычисляется по формуле

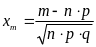. (9.2)

Функция Гаусса обладает свойством четности , поэтому в таблице Приложения 1 приведены ее значения только для положительных аргументов. Кроме того, эта функция – быстро убывает, поэтому для значений аргументов, больших 4 можно принимать .

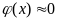Поскольку число испытаний n велико, вероятность достичь появления события А определенное число раз достаточно мала. Кроме того, вероятность достижения непрерывно распределенной случайной величиной определенного значения теоретически равна 0. Эти обстоятельства делают формулу (9.1) мало применимой на практике. Практически значимые результаты дает формула вероятности попадания случайной величины на участок, следующая из интегральной теоремы Лапласа:

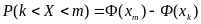, (9.3)

где Ф(х) – нормированная функция Лапласа

.

Лапласа сведены в таблицу в Приложении 2. Аргументы функции Лапласа 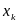и вычисляются по формуле (9.2).

Функция Лапласа обладает свойством нечетности , поэтому в таблице Приложения 2 приведены ее значения только для положительных аргументов. Кроме того, для значений аргументов, больших 5 можно полагать . Соответственно

. (9.4)

9.2. Пример решения типового задания по теме «Локальная и интегральная теоремы Лапласа» 例题详解

Задание № 9. 34% студентов не могут сдать экзамен по курсу «Статистика» с первого раза. Какова вероятность, что из 254 студентов смогли сдать экзамен с первого раза:有34%的学生不能第一次就通过统计考试，求出有254名学生第一次就能通过考试的概率：

1. 168 студентов,

2. от 150 до 170 студентов,

3. больше 160 студентов,

4. меньше 120 студентов.

Решение. Случайное событие А – студент сдал экзамен по статистике с первого раза. Случайная величина Х - число студентов, сдавших этот экзамен с первого раза. Определим значения параметров задачи: n = 254, q = 0,34, р = 1 – q = 1 – 0,34 = 0,66. Обратим внимание, что в задаче рассматриваются студенты, которые сдают экзамен с первого раза, т.е. в условии приведена вероятность противоположного события q. 随机事件A－学生第一次就能通过统计考试。随机变量X－第一次通过考试的学生数量。一次确定各参数值n = 254, q = 0,34, р = 1 – q = 1 – 0,34 = 0,66.同时注意，因为该题是分析第一次通过考试的学生，所以该条件决定对立事件概率值q。

Найдем вероятность события Х = m = 168. Используем формулу (9.2):

По таблице Приложения 1 можем найти значение функции Гаусса только в ближайшей к 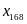точке х = 0,05: .

Значит .

Найдем вероятности попадания случайной величины Х на интервалы. Используем формулу (9.3):

.

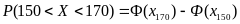Значения аргументов найдем по формуле (9.2):

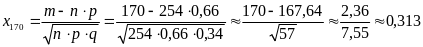
По таблице Приложения 1 можем найти значение функции Лапласа:

,

.

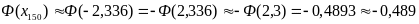Тогда

= 0,122 + 0,489 = 0,611.

Аналогично по формуле (9.3) находим оставшиеся вероятности, а аргументы функции Лапласа – по формуле (9.2):

,

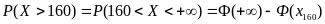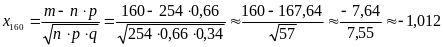
Значение функции Лапласа находим по таблице Приложения 2:

,

согласно соотношению (9.4).

Тогда

.

Аналогично:

,

,

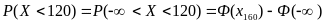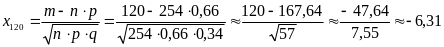, т.к. 6,31 > 5, ,

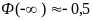согласно соотношению (9.4).

Тогда

.

Полученные данные подтверждаются основными характеристиками нормального распределения. Действительно, четко выраженный максимум в точке математического ожидания делает маловероятным, например, попадание значений случайной величины на полуинтервал . Это следует и из известного «правила », которое утверждает, что попадание значений случайной величины за пределы интервала 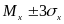маловероятно. Проверим это утверждение.

Найдем дисперсию случайной величины Х:

.

Средне квадратическое отклонение

.

Тогда и ,

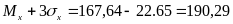. Очевидно, что число 120 лежит за пределами интервала : , т.е. маловероятно, практически невозможно, что случайная величина Х принимает значения, меньшие 120.