6. Дайте определение понятий «единичная ступенчатая функция» и «единичная импульсная функция». Опишите их свойства.

Единичная ступенчатая функция— специальная математическая функция, чьё значение равно нулю для отрицательных аргументов и единице для положительных аргументов.

Единичная импульсная функция равна нулю при всех значениях аргумента, отличных от нуля, но при нулевом значении аргумента она обращается в бесконечность. 

Единичная импульсная функция является производной от единичной ступенчатой функции, а единичная ступенчатая функция-интегралом от единичной импульсной функции. Следовательно, вводится понятие производной от функции в точке ее разрыва.

Единичная импульсная функция - Реакция звена на единичный импульс

Единичная ступенчатая функция 1(t), называемая также функцией Хевисайда или функцией включения имеет значения: 

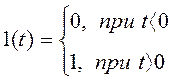
и обычно неопределенна при t=0.График функции имеет вид

        

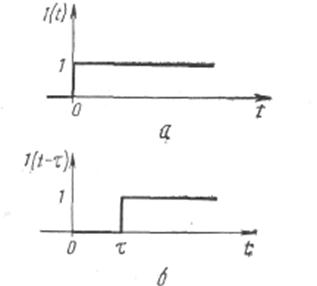
2) импульсная функция (δ–функция Дирака)  (рис.11 б)

                                                   

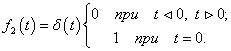
 Импульсная функция представляет собой «идеальный импульс», ширина основания которого стремится к нулю, а высота – к бесконечности.

7. Какой вид имеет частотный спектр единичной ступенчатой функции и единичной импульсной функции.

Преобразование F(jw, c) носит название обобщенного преобразования Фурье. Для получения спектра единичной функции перейдем к пределу:

Единичная импульсная функция:

Таким образом, d-функция имеет равномерный амплитудный и нулевой фазовый спектры. Равенство нулю на всех частотах фазового спектра означает, что все гармонические составляющие d-функции, суммируясь с нулевыми начальными фазами, образуют при t = 0 пик бесконечно большого значения.

8. Как определяется ширина сплошного частотного спектра и ширина дискретного частотного спектра.

Ширина спектра апериодического сигнала определяется, как часть спектра, в которой сосредоточена заданная доля (90 или 95%) энергии сигнала.

Решение этой задачи основано на теореме Релея – равенстве Парсеваля интеграла Фурье. В соответствии с этой теоремой распределение энергии риодического сигнала по частоте можно определить из выражения :

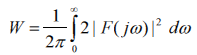
Ширина спектра сигнала (F) это диапазон частот, в пределах которого сосредоточена его основная энергия. Она определяет скорость изменения сигнала внутри интервала его существования

Как видно из диаграмм спектр ПППИ является дискретным и неограниченным. Поэтому за ширину спектра принимают диапазон частот, в пределах которого находится два первых лепестка, т. к. в них содержится около 95% энергии сигнала:

9. Как связана ширина частотного спектра сигнала с длительностью (шириной) сигнала.

База сигнала есть произведение длительности сигнала на ширину его спектра . Необходимо отметить, что между шириной спектра и длительностью сигнала существует обратно пропорциональная зависимость: чем короче спектр, тем больше длительность сигнала. Таким образом, величина базы остается практически неизменной;