- •7. Побудова спряженої кореляційно-регресійної моделі
- •8. Геометрична інтерпретація спряжених моделей
- •9. Обчислення тангенса кута між спряженими лініями
- •9. Обчислення тангенса кута між спряженими лініями
- •10. Перевірка формули декомпозиції загальної дисперсії результуючої змінної
- •11. Обчислення стандартної похибки моделі
- •12. Побудова довірчих інтервалів для оцінки фактичного результуючої змінної, їх геометрична інтерпретація
- •13. Розрахунок теоретичного та емпіричного значень відношення детермінації, їх економічна інтерпретація. Обчислення кореляційного відношення
- •14. Обчислення вибіркових похибок параметрів регресії. Побудова довірчих інтервалів для істинних значень параметрів регресії, їх геометрична інтерпретація.
- •15. Розрахунок вибіркової похибки моделі. Побудова довірчого інтервалу для середнього прогнозного значення результуючої змінної, його геометрична інтерпретація.
- •16. Обчислення похибки індивідуального прогнозу. Побудова довірчого інтервалу для індивідуального прогнозного значення результуючої змінної, його геометрична інтерпретація.
- •17. Оцінка коефіцієнта кореляції.
- •18. Перевірка статистичної значущості параметрів зв’язку між змінними.
- •19. Експрес-діагностика моделі.
- •20. Економічна інтерпретація результатів економетричного дослідження та їх використання
Міністерство освіти і науки України
Львівський національний університет імені Івана Франка
Економічний факультет
«ІНДЗ №6»
(7-20)
Виконав:
студент групи Екф-23
Гоцій М.І.
Перевірив:
ас.Панчишин А.І.
Львів 2013
7. Побудова спряженої кореляційно-регресійної моделі
Спряжене рівняння регресії відносно рівняння ỹ = b0+b1x буде мати вигляд:
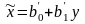
Система нормальних рівнянь, коренями якої є параметри b'0 та b'1, має вигляд:
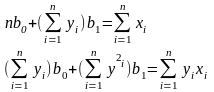
Отримуємо такі результати:
b0' |
9 234, 122 |
b1' |
2,322 |
Звідси, спряжена парна лінійна кореляційно-регресійна модель матиме вигляд:
х=9 234, 122+2,322* у
Коефіцієнт регресії спряженої моделі b1'= 2,322 показує, що при збільшенні величини Введення в дію основних засобів у факт. Цінах на 1 млн грн. середнє значення величини дебіторської заборгованості повинно в середньому зрости на 2,322 млн грн..
Знаходимо коефіцієнт кореляції між двома величинами:
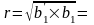 0,923
0,923
Значення коефіцієнта кореляції співпадає з попередніми результатами обчислень.
8. Геометрична інтерпретація спряжених моделей
Спряжені рівняння регресії мають такі властивості:
якщо кореляційний взаємозв’язок між змінними х та у відсутній, то спряжені рівняння регресії зображуються двома перпендикулярними прямими, де
 ;
;якщо між змінними х та у існує функціональний зв'язок то обидві спряжені лінії регресії співпадають;
С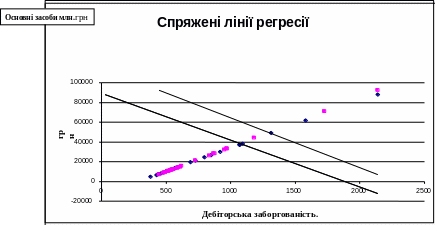 пряжені
моделі графічно відображаються двома
прямими, що перетинаються в точці,
координатами якої є середні значення
змінних.
пряжені
моделі графічно відображаються двома
прямими, що перетинаються в точці,
координатами якої є середні значення
змінних.
9. Обчислення тангенса кута між спряженими лініями
Якщо між змінними х та у існує кореляційний зв’язок, то спряжені лінії регресії перетинаються, утворюючи між собою гострий кут α.
tg
φ =
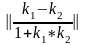
k1= b1
k2=1/b1`
tg φ = 0,001203493
φ= 0°4ʹ
Оскільки прямі утворюють гострий кут, то зв'язок між змінними дуже тісний.
9. Обчислення тангенса кута між спряженими лініями
Якщо між змінними х та у існує кореляційний зв’язок, то спряжені лінії регресії перетинаються, утворюючи між собою гострий кут α.
tg φ =
k1= b1
k2=1/b1`
tg φ = 0,001203493
φ= 0°4ʹ
Оскільки прямі утворюють гострий кут, то зв'язок між змінними дуже тісний.
10. Перевірка формули декомпозиції загальної дисперсії результуючої змінної

|
|
|
|
Σ |
837464573 |
564758642 |
272705931 |
Формула декомпозиції загальної дисперсії:
 ,
,
де – загальна дисперсія результуючої
змінної;
– загальна дисперсія результуючої
змінної;
 – дисперсія теоретичних значень
результуючої змінної (пояснена дисперсія);
– дисперсія теоретичних значень
результуючої змінної (пояснена дисперсія);
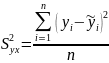 – дисперсія випадкових відхилень
(непояснена дисперсія).
– дисперсія випадкових відхилень
(непояснена дисперсія).
 .
Відповідно підставляємо дані у формулу,
n
=25
.
Відповідно підставляємо дані у формулу,
n
=25
33498582,92 = 22590345,68+10908237,24
Дана тотожність справджується.
Чим більша пояснена дисперсія і, відповідно, менша непояснена, тим точніше кореляційно-регресійна модель пояснює зв’язок між змінними. Тому можна зробити висновок, що дана модель достатньо точно пояснює зв’язок між факторною і результуючою змінними .
11. Обчислення стандартної похибки моделі
Стандартна похибка моделі характеризує розсіювання фактичних значень результуючої змінної навколо теоретичних, знайдених за допомогою рівняння регресії.
Стандартною похибкою кореляційно-регресійної моделі називається величина:


Стандартна похибка моделі має ті ж одиниці вимірювання, що і результуюча змінна. Вона є мірою непоясненої варіації у загальній дисперсії.
1. Якщо кореляційний зв'язок між результуючою змінною і факторною ознакою відсутній, то:

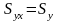
тобто стандартна похибка моделі дорівнює стандартному квадратичному відхиленню результуючої змінної.
2. Якщо взаємозв’язок х та у – функціональний, всі випадкові відхилення рівні 0, то
 .
.
Провівши розрахунки, ми одержали:

Дане значення повинне лежати в інтервалі 0≤ Syx ≤ Sy
Оскільки, Sy= 28938,98017 , то обчислення правильні.