
- •3.Жинақталатын күштер жүесінің тепе-тендік шарты мен теңдеулері. Статика есептерін шешудің жалпы әдісі.
- •4.Күштің нүктеге қатысты моменті және оның қасиеттері. Рычаг және оның тепе-тендік шарты мен теңдеуі. Күштің нүктеге қатысты моментінің векторы.
- •5.Екі параллель күштер жүйесін тең әсер етуші күшке келтіру. Параллель күштер центрі.
- •6.Қос күш. Қос күш моменті. Қос күш моментінің векторы. Қос күштерді қосу.
- •7. Күшті параллель тасымалдау туралы теорема(Пуансо леммасы). Күштердің кез келген жазық жүйесін берілген центрге келтіру. Бас вектор және бас момент.
- •8. Күштердің кез келген жазық жүйесін келтірудің дербес жағдайлары. Күштердің кез келген жазық жүйесі үшін Вариньон теоремасы.
- •9.Күштердің кез келген жазық жүйесінің тепе-тендік шарты мен теңдеулері. Параллель күштердің жазық жүесінің тепе-тендік теңдеулері.
- •10. Сырғанау үйкелісі және оның зандары. Үйкеліс бұрышы. Домалау үйкелісі.
- •11. Қатты дененің ауырлық центрі. Біртекті денелердің ауырлық центрінің координаталарын анықтау. Ауырлық центрін табу эдістері.
- •13)Дененің бұрыштық жылдамдығы мен үдеуі.
- •14. Айналмалы қозғалыстағы дене нүктелерінің жылдамдықтары мен үдеулері.
- •15.Қатты дененің жазық параллель қозғалысының теңдеуі. Жазық фигура қозғалысының тасымал-ілгерілемелі және полюс айналасында салыстырмалы айналмалы қозғалыстарға жіктеу.
- •16.Өз жазықтығында қозғалып бара жатқан жазық фигура нүктелерінің жылдамдықарың анықтау.
- •17.Өз жазықтығында қозғалып бара жатқан жазық фигура нүктелерінің үдеулерін анықтау.
- •18. Инерция күші туралы ұғым. Материалық нүкте үшін Даламбер принципі
- •19. Қисық сызықты қозғалыстағы айнымалы күштін жұмысы. Тең әсер етуші күштін жұмысы туралы теорема. Ауырлық күшінің жұмысы.
- •20. Күш қуаты. Пайдалы әсер коэффициенті. Дененің тұрақты өстен айналысқа келтіретін күштін жұмысы мен қуаты.
- •22)Материялық нүктенің кинетикалық энергиясының өзгеру туалы теорема.Механикалық энергияның сақталу заңы.
- •23)Механикалық жүйе туралы ұғым.Әсер ететін күштер.
- •24.Дененің тұрақты өстен айналмалы қозғалысының теңдеуі. Біртекті денелердің инерция моменттерін есептеуге арналған мысалдар.
- •25. Қатты дененің кинетикалық энергиясы.
- •26.Қиманың статикалық моменті.Қималардың инерция моменті.Параллель осьтерге қатысты инерция моменті.
- •27. Қарапайым қималардың инерция моменттері: Тік төртбұрыш. Үшбұрыш. Дөңгелек
- •28) Бұрылған өстерге қатысты инерция моменттері. Басты өстер және басты инерция моменттері.
- •29.Ішкі күштер. Қию әдісі. Кернеу.
- •31. Бойлық күш. Білеудің қөлденең және қөлбеу қималарындағы кернеулер.Бойлық және қөлденен деформациялар.
- •32)Созу мен сығу диаграммалары.
- •33. Мүмкіндік кернеулер. Беріктікке есептеу. Статикалық анықталмаған жүйелер.
- •34. Жазық кернеулі күй.
- •35.Таза ығысу.Таза ығысудағы деформация мен Гук заңы.
- •36. Буралу, негізгі түсініктер. Бұралу моменті. Қимасы дөңгелек тік білеудің бұралуы.
- •37. Бұралған біліктегі деформация мен орын ауыстыру. Бұралудағы статикалық анықталмаған жүйелер.
- •38.Иілу.Ішкі күштердің эпюралары.
- •39. Ию моменті, қолденең күш, таралған күш қарқындылығы арасындағы дифференциалдық байланыс.
- •40)Таза иілу.
- •41. Көлденең иілу
- •42.Иілудегі басты кернеулер.
- •43. Арқалық қималардың иілуі мен бұралуы.
- •44.Қимасы дөңгелек білеудің иіліп бұралуы.
- •46.Сырық ұштарының бекітілу әсері.Эйлер формуласын қолдану шегі.
- •47. Сығылған сырықтарды орнықтылыққа есептеу.
13)Дененің бұрыштық жылдамдығы мен үдеуі.
Егер
қозғалыстағы дененің кем дегенде екі
нүктесі қозғалмайтын болса онда мұндай
дене тұрақты өстен айналмалы қозғалыста
болады.Осы қозғалмаитын нүктелер арқылы
жүргізілген түзудің барлық нүктелері
тыныштық қалпын сақтайды және ол айналу
өсі деп аталады.Дененің кез келген t
уақыттағы орнын анықтайтын ,бұдан былай
айналу бұрышы немесе бұрыштық координатасы
деп аталатын жазық ϕ бұрышы мен уақыттың
арасындағы байланыс. ϕ = ϕ(t);дененің
қозғалмайтын өстен айналмалы қозғалысының
теңдеуі немесе айналу заңы болып
табылады.Нгер ∆t уақыт аралығындағы ϕ
бұрышының өсімшесі ∆ϕ болса,онда мына
қатнас ∆ϕ/∆t=ωорт(1);Дененің
осы уақыт аралығындағы орташа бұрыштық
жылдамдығы д.а.Осы шаманың ∆t->0 шегі,
яғни
 ;
дененің берілген уақыттағы бұрыштық
жылдамдығы немесе дененің айналмалы
қозғалысының бұрыштық жылдамдығы
д.а.Бұрыштық жылдамдықтың бағыты
;
дененің берілген уақыттағы бұрыштық
жылдамдығы немесе дененің айналмалы
қозғалысының бұрыштық жылдамдығы
д.а.Бұрыштық жылдамдықтың бағыты
 туындысы таңбасымен анықталады.Сонымен
бұрыштық жылдамдық дененің бірлік
уақыттағы айналу бұрышының өзгеру
шапаңдығын сипаттайтын шама екенін
көреміз.Бұрыштық жылдамдық
туындысы таңбасымен анықталады.Сонымен
бұрыштық жылдамдық дененің бірлік
уақыттағы айналу бұрышының өзгеру
шапаңдығын сипаттайтын шама екенін
көреміз.Бұрыштық жылдамдық
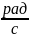 немесе
радиан өлшемсіз шама болғандықтан
немесе
радиан өлшемсіз шама болғандықтан
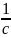 пен өлшенеді.Қатты дененің бұрыштық
жылдамдығын айналу өсінің бойымен
бағытталатын вектор түрінде қарастыруға
болады.
пен өлшенеді.Қатты дененің бұрыштық
жылдамдығын айналу өсінің бойымен
бағытталатын вектор түрінде қарастыруға
болады.
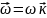 ;
;
Мұндағы
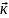 -өс
бойымен бағытталған бірлік орт.
-өс
бойымен бағытталған бірлік орт.
 векторының бағыты оң бұранда ережесімен
анықталады.Сонымен
векторы айналу өсінде жатады да, оның
кезкелген нүктесінде әсер етеді деп
саналады,яғни бұрыштық жылдамдық векторы
сырғымалы вектор болып саналады.Егер
бұрыштық жылдамдықтың шамасы өсетін
болса онда
векторы айналу өсі бойымен В нүктесінен
С нүктесіне қарай бағытталады.ал азаятын
боса онда бұрыштық жылдамдық векторы
кері қарай бағытталады.Олай болса
бұрыштық жылдамдықтың векторы кез
келген уақыт кезеңінде дененің айналу
өсін,дененің осы өстен айналу бағытын
және дененің бұрыштық жылдамдығының
модулін анықтайды.
векторының бағыты оң бұранда ережесімен
анықталады.Сонымен
векторы айналу өсінде жатады да, оның
кезкелген нүктесінде әсер етеді деп
саналады,яғни бұрыштық жылдамдық векторы
сырғымалы вектор болып саналады.Егер
бұрыштық жылдамдықтың шамасы өсетін
болса онда
векторы айналу өсі бойымен В нүктесінен
С нүктесіне қарай бағытталады.ал азаятын
боса онда бұрыштық жылдамдық векторы
кері қарай бағытталады.Олай болса
бұрыштық жылдамдықтың векторы кез
келген уақыт кезеңінде дененің айналу
өсін,дененің осы өстен айналу бағытын
және дененің бұрыштық жылдамдығының
модулін анықтайды.
Бұрыштық
үдеу.Егер ∆t ауқыт аралығында бұрыштық
жылдамдық өсімшесі ∆ω болса онда
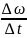 εорт
шамасы дененің осы уақыт аралығындағы
орташа бұрыштық үдеуі деп аталады.Осы
шаманың ∆t→0 шегі яғни
εорт
шамасы дененің осы уақыт аралығындағы
орташа бұрыштық үдеуі деп аталады.Осы
шаманың ∆t→0 шегі яғни
 дененің берілген уақыттағы бұрыштық
үдеуі д.а. Бұрыштық үдеудің бағыты
дененің берілген уақыттағы бұрыштық
үдеуі д.а. Бұрыштық үдеудің бағыты
 туындысы таңбасымен анықталады.Сонымен
бұрыштық үдеу дененің бірлік уақыттағы
бұрыштық жылдамдығының өзгеру шапшаңдығын
сипаттайтын шама екенін көреміз.Бұрыштық
үдеудің өлшемі
туындысы таңбасымен анықталады.Сонымен
бұрыштық үдеу дененің бірлік уақыттағы
бұрыштық жылдамдығының өзгеру шапшаңдығын
сипаттайтын шама екенін көреміз.Бұрыштық
үдеудің өлшемі
 немесе
немесе
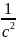 .
Бұрыштық үдеу айналу өсінің бойымен
бағытталған
.
Бұрыштық үдеу айналу өсінің бойымен
бағытталған
 =
=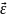 векторымен өрнектеуге болады.Дененің
үдемелі айнымалы қозғалысында
және
векторлары бағыттас ,ал кемімелі
қозғалысында қарама-қарсы болады.
векторымен өрнектеуге болады.Дененің
үдемелі айнымалы қозғалысында
және
векторлары бағыттас ,ал кемімелі
қозғалысында қарама-қарсы болады.
14. Айналмалы қозғалыстағы дене нүктелерінің жылдамдықтары мен үдеулері.
Айналу z өсінен h қашықтықтығында М нүктесін қарастырайық (10.4,10.5-сурет).Дене айналғанда М нүктесі радиусы h-қа тең жазықтығы айналу өсіне перпендикуляр болатын шеңбер сызады.Бұл шеңбердің О центрі айналу өсінде жатады.М нүктесінің өзінің траекториясындағы орнын қозғалмайтын Q жазықтығында (10.3-сурет )жататын бір А нүктесінен есептелінетін s доғалық координатасымен анықтаймыз.s доғасы есептелуінің оң бағыты ретінде айналу φ бұрышының оң бағыты қабылданады.
Онда s доғасының ұзындығы
S=hφ=hφ(t) (10.13)
Формуласымен анықталады.М нүктесінің жылдамдығы (9.26) формула бойынша
VM=ds/dt=hdφ/dt=hω (10.14)
М нүктесінің осы жылдамдығы нүктенің сызықтық жылдамдығы деп аталады. Сонымен,айналмалы қозғалыстағы дене нүктесінің сызықтық жылдамдығы дененің бұрыштық жылдамдығы мен нүктенің айналу өсіне дейінгі қашықтығының көбейтіндісіне тең.Сызықтық жылдамдық векторы шеңбердің М нүктесінен жүргізілген жанаманың бойымен айналу бағытына қарай бағытталады.Бұрыштық жылдамдық тұтас дененің кинематикалық сипаттамасы болатындықтан (10.14)формула бойынша айналмалы қозғалыстағы дене нүктелерінің жылдамдықтары осы нүктелердің айналу өсіне дейінгі қашықтықтарына пропорционал болады
