
- •3.Жинақталатын күштер жүесінің тепе-тендік шарты мен теңдеулері. Статика есептерін шешудің жалпы әдісі.
- •4.Күштің нүктеге қатысты моменті және оның қасиеттері. Рычаг және оның тепе-тендік шарты мен теңдеуі. Күштің нүктеге қатысты моментінің векторы.
- •5.Екі параллель күштер жүйесін тең әсер етуші күшке келтіру. Параллель күштер центрі.
- •6.Қос күш. Қос күш моменті. Қос күш моментінің векторы. Қос күштерді қосу.
- •7. Күшті параллель тасымалдау туралы теорема(Пуансо леммасы). Күштердің кез келген жазық жүйесін берілген центрге келтіру. Бас вектор және бас момент.
- •8. Күштердің кез келген жазық жүйесін келтірудің дербес жағдайлары. Күштердің кез келген жазық жүйесі үшін Вариньон теоремасы.
- •9.Күштердің кез келген жазық жүйесінің тепе-тендік шарты мен теңдеулері. Параллель күштердің жазық жүесінің тепе-тендік теңдеулері.
- •10. Сырғанау үйкелісі және оның зандары. Үйкеліс бұрышы. Домалау үйкелісі.
- •11. Қатты дененің ауырлық центрі. Біртекті денелердің ауырлық центрінің координаталарын анықтау. Ауырлық центрін табу эдістері.
- •13)Дененің бұрыштық жылдамдығы мен үдеуі.
- •14. Айналмалы қозғалыстағы дене нүктелерінің жылдамдықтары мен үдеулері.
- •15.Қатты дененің жазық параллель қозғалысының теңдеуі. Жазық фигура қозғалысының тасымал-ілгерілемелі және полюс айналасында салыстырмалы айналмалы қозғалыстарға жіктеу.
- •16.Өз жазықтығында қозғалып бара жатқан жазық фигура нүктелерінің жылдамдықарың анықтау.
- •17.Өз жазықтығында қозғалып бара жатқан жазық фигура нүктелерінің үдеулерін анықтау.
- •18. Инерция күші туралы ұғым. Материалық нүкте үшін Даламбер принципі
- •19. Қисық сызықты қозғалыстағы айнымалы күштін жұмысы. Тең әсер етуші күштін жұмысы туралы теорема. Ауырлық күшінің жұмысы.
- •20. Күш қуаты. Пайдалы әсер коэффициенті. Дененің тұрақты өстен айналысқа келтіретін күштін жұмысы мен қуаты.
- •22)Материялық нүктенің кинетикалық энергиясының өзгеру туалы теорема.Механикалық энергияның сақталу заңы.
- •23)Механикалық жүйе туралы ұғым.Әсер ететін күштер.
- •24.Дененің тұрақты өстен айналмалы қозғалысының теңдеуі. Біртекті денелердің инерция моменттерін есептеуге арналған мысалдар.
- •25. Қатты дененің кинетикалық энергиясы.
- •26.Қиманың статикалық моменті.Қималардың инерция моменті.Параллель осьтерге қатысты инерция моменті.
- •27. Қарапайым қималардың инерция моменттері: Тік төртбұрыш. Үшбұрыш. Дөңгелек
- •28) Бұрылған өстерге қатысты инерция моменттері. Басты өстер және басты инерция моменттері.
- •29.Ішкі күштер. Қию әдісі. Кернеу.
- •31. Бойлық күш. Білеудің қөлденең және қөлбеу қималарындағы кернеулер.Бойлық және қөлденен деформациялар.
- •32)Созу мен сығу диаграммалары.
- •33. Мүмкіндік кернеулер. Беріктікке есептеу. Статикалық анықталмаған жүйелер.
- •34. Жазық кернеулі күй.
- •35.Таза ығысу.Таза ығысудағы деформация мен Гук заңы.
- •36. Буралу, негізгі түсініктер. Бұралу моменті. Қимасы дөңгелек тік білеудің бұралуы.
- •37. Бұралған біліктегі деформация мен орын ауыстыру. Бұралудағы статикалық анықталмаған жүйелер.
- •38.Иілу.Ішкі күштердің эпюралары.
- •39. Ию моменті, қолденең күш, таралған күш қарқындылығы арасындағы дифференциалдық байланыс.
- •40)Таза иілу.
- •41. Көлденең иілу
- •42.Иілудегі басты кернеулер.
- •43. Арқалық қималардың иілуі мен бұралуы.
- •44.Қимасы дөңгелек білеудің иіліп бұралуы.
- •46.Сырық ұштарының бекітілу әсері.Эйлер формуласын қолдану шегі.
- •47. Сығылған сырықтарды орнықтылыққа есептеу.
6.Қос күш. Қос күш моменті. Қос күш моментінің векторы. Қос күштерді қосу.
Шамалары
тең, бағыттары параллель, қарама-қарсы
және әсер ету сызықтары бір түзудің
бойында жатпайтын
 күштер жүйесі (1-сурет) қос күш немесе
күштер жұбы деп аталады. Мұндай күштер
жұбы,яғни екі күштен құралатын жүйе тең
әсер етуші күшке келтірілмейді және
тепе-теңдікте болмайды. Қос күшті бір
күшпен теңгеруге болмайды.
күштер жүйесі (1-сурет) қос күш немесе
күштер жұбы деп аталады. Мұндай күштер
жұбы,яғни екі күштен құралатын жүйе тең
әсер етуші күшке келтірілмейді және
тепе-теңдікте болмайды. Қос күшті бір
күшпен теңгеруге болмайды.
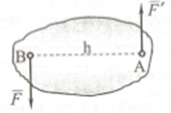 1-сурет
1-сурет
Қос күш орналасқан жазықтықты қос күш әсерінің жазықтығы, ал жұп күштерінің әсер ету сызықтарының арасындағы ең қысқа қашықтық h қос күш иіні деп аталады. Қос күштің денені айналдыру қабілеті жұп күштерінің шамасы және h иініне тікелей байланысты қос күш моментімен сипатталады. Қос күш моментінің шамасы оң немесе теріс таңбамен алынған күш модулі мен иіннің көбейтіндісіне тең. Қос күш моментін М немесе М деп белгілейміз. Онда
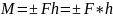
Егер қос күш денені сағат тілі айналысына кері бағытта айналдыруға тырысса жұп моментінің таңбасы оң, ал сағат тілі айналысымен бағыттас айналдыруға тырысса теріс деп есептелінеді.
Қос
күштің денені айналдыру қабілеті
векторлық шама болатын
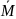 жұп моментімен (2-сурет) сипатталады.
Қос күш моментінің векторы оның бір
күшінің екінші күш түсірілген нүктеге
қатысты алынған моментіне тең:
жұп моментімен (2-сурет) сипатталады.
Қос күш моментінің векторы оның бір
күшінің екінші күш түсірілген нүктеге
қатысты алынған моментіне тең:
 (
)=
(
)= немесе
немесе
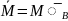 (
)=
(
)=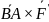
Қос күш моментті векторының:
1.модулі
жұп күшінің иінге көбейтіндісіне тең,
яғни
 ;
;
2.
векторы қос күштің әсер ету жазықтығына
перпендикуляр бағытталған түзудің
бойында орналасқан, 2-суретте
, күштері xOy жазықтығында орналасқан, ал
векторы Оz өсіне параллель бағытталған;
күштері xOy жазықтығында орналасқан, ал
векторы Оz өсіне параллель бағытталған;
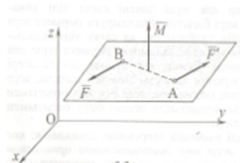 (2-сурет)
(2-сурет)
3.осы түзудің бойымен бағытталған векторының ұшынан қарағанда қос күштің денені айналдыру бағыты сағат тілі айналысына қарама-қарсы бағытта көрінетіндей болуы қажет. Вектор моменттері тең қос күштер бір-біріне балама болады.
Қос күштерді қосу:
Қатты денеге вектор моменттері
 бір жазықтықта орналасқан қос күштер
жүйесі әсер ететін болсын.
бір жазықтықта орналасқан қос күштер
жүйесі әсер ететін болсын.
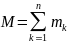
Жазықтықта орналасқан қос күштер жүйесі тепе-теңдікте болу үшін,қос күш моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті.

Қатты денеге бір жазықтықта жатпайтын моменттері
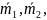 қос күштер жүйесі әсер ететін болсын.
қос күштер жүйесі әсер ететін болсын.
Әр
түрлі жазықтықтарда орналасқан қос
күштер жүйесі тепе-теңдікте болу үшін
тең әсерлі қос күш вектор –моменті
нөлге тең болуы қажет,яғни кеңістік
жұптар жүйесінің тепе-теңдік шарты
мынадай түрде жазылады:
 неемсе
неемсе
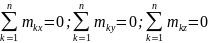
Сонымен, әр түрлі жазықтықтарда жататын қос күштер жүйесі тепе-теңдікте болу үшін құраушы қос күш моменттерінің координаталар өстеріне проекцияларынығ алгебралық қосындылары жеке-жеке нөлге тең болуы қажет және жеткілікті.
7. Күшті параллель тасымалдау туралы теорема(Пуансо леммасы). Күштердің кез келген жазық жүйесін берілген центрге келтіру. Бас вектор және бас момент.
Күштердің кез келген жазық жүйесін берілген центрге келтіру. Бас вектор жіне бас момент.
Қатты
дененің
 нүктелеріне түсірілген
нүктелеріне түсірілген
 күштері бір жазықтықта орналасқан
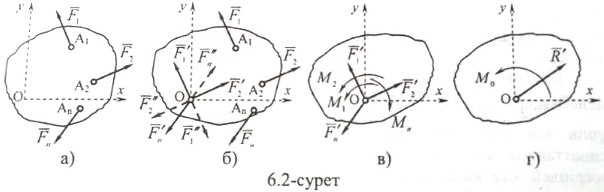
болсын (6.2,а-сурет). Күштер жүйесінің
әсер ету жазықтығында орналасқан кез
келген О нүктесін келтіру центрі деп
алып, Пуансо леммасы негізінде барлық
әсер етуші күштерді О нүктесіне өздеріне
параллель (6.2,б-сурет) көшірейік. Онда
күштері бір жазықтықта орналасқан
болсын (6.2,а-сурет). Күштер жүйесінің
әсер ету жазықтығында орналасқан кез
келген О нүктесін келтіру центрі деп
алып, Пуансо леммасы негізінде барлық
әсер етуші күштерді О нүктесіне өздеріне
параллель (6.2,б-сурет) көшірейік. Онда
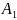 нүктесіне түсірілген
күші О нүктесінде түсірілген
нүктесіне түсірілген
күші О нүктесінде түсірілген
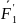 күшіне және моменті
күшіне және моменті
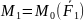 қосылған (
қосылған (
 )қос күшке балама болады.
)қос күшке балама болады. нүктесіне түсірілген
нүктесіне түсірілген
 күші
О нүктесінде түсірілген
күші
О нүктесінде түсірілген
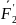 күшіне және моменті
күшіне және моменті
 қосылған (
қосылған (
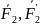 ) қос күшке балама болады. Осындай ретпен
барлық күштерді параллель тасымалдаудың
нәтижесінде О центріне түсірілген
) қос күшке балама болады. Осындай ретпен
барлық күштерді параллель тасымалдаудың
нәтижесінде О центріне түсірілген
=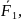
 (6.1)
(6.1)
күштер жүйесі мен бір жазықтықта орналасқан моменттері
,
, …,
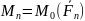 (6.2)
(6.2)
қосылған

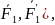
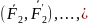
 қос күштер (6.2,в-сурет) жүйесін аламыз.
қос күштер (6.2,в-сурет) жүйесін аламыз.
Күштер
көпбұрышы ережесі бойынша О нүктесіне
түсірілген
 күштерін қосып
күштерін қосып олардың тең ісер етуші күшін
табамыз(6.2,г-сурет):
олардың тең ісер етуші күшін
табамыз(6.2,г-сурет):
 (6.3)
(6.3)
(6.1)
теңдіктерді ескере отырып (6.3) теңдіктің
оң жағын
 күштері
арқылы өрнектейміз:
күштері
арқылы өрнектейміз:
 (6.4)
(6.4)
Денеге әсер ететін күштердің геометриялық қосындысына тең болатын векторын күштердің кез келген жазық жүйесінің бас векторы деп атаймыз.
Бір жазықтықта орналасқан қос күштерді қосу ережесі бойынша (5.4 формула) барлық қосылған қос күштер жүйесін осы жазықтықта орналасқан бір қорытынды (тең әсерлі) қос күшке келтіреміз. Осы тең әсерлі қос күштің моменті (6.2) теңдіктері бойынша:
 (6.5)
(6.5)
Әсер
етуші күштердің келтіру О центріне
қатысты алынған моменттерінің алгебралық
қосындысына тең
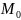 шамасын
жүйенің бас моменті деп атайды.
шамасын
жүйенің бас моменті деп атайды.
Сонымен, қатты денеге әсер ететін күштердің кез келген жазық жүйесін келтіру центріне түсірілген осы жүйенің бас векторына тең бір күш пен моменті күштер жүйесінің келтіру центріне қатысты бас моментіне тең қос күшке келтіруге болады (6.2,г-сурет), яғни
 ,
(6.6)
,
(6.6)
Күштер жүйеснің бас векторының модулі мен бағытын күштер көпбұрышын құру арқылы немесе аналитикалық әдіспен жинақталатын күштер жүйесінің тең әсер етуші күшінің модулі мен бағытын анықтайтын (2.4) және (2.5) формулаларымен анықтауға болады.
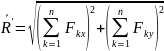 (6.7)
(6.7)
 (6.8)
(6.8)
Қатты денеге әсер етуші күштердің барлығы келтіру центріне параллель тасымалданатындықтан бас векторының модулі мен бағыты келтіру центрінің орнына тәуелсіз яғни инвариантты болады.
Бас моменттің модулі мен таңбасы (6.5) формуласымен анықталады. Келтіру центрінің орны өзгерген сайын жүйе күштерінің де моменттері өзгеріп отырады. Олай болса бас моменттің модулі мен таңбасы да өзгеріп отырады.
Сонымен
қатар мына жағдайды атап кеткен жөн
болады. Қатты денеге әсер етуші
 күштерінің
бас векторы
күштер жүйесі үшін тең әсер етуші күш
бола алмайды, өйткені ол бас моментті
сипаттайтын қос күшсіз жалғыз өзі денеге
берілген күштер жүйесінің әсеріндей
әсер жасай алмайды. Оған қосымша, бас
векторды еркін вектор деп қарастыруға
болса (бас вектордың әсер ету нүктесінен
кез келген орында алуға болады), ал тең
әсер етуші күштің векторы өзінің белгілі
бір әсер ету сызығының бойымен ғана
бағытталатын сырғымалы вектор болады.
күштерінің
бас векторы
күштер жүйесі үшін тең әсер етуші күш
бола алмайды, өйткені ол бас моментті
сипаттайтын қос күшсіз жалғыз өзі денеге
берілген күштер жүйесінің әсеріндей
әсер жасай алмайды. Оған қосымша, бас
векторды еркін вектор деп қарастыруға
болса (бас вектордың әсер ету нүктесінен
кез келген орында алуға болады), ал тең
әсер етуші күштің векторы өзінің белгілі
бір әсер ету сызығының бойымен ғана
бағытталатын сырғымалы вектор болады.
