44.Қимасы дөңгелек білеудің иіліп бұралуы.

Білектерді есептегенде,иіліп бұралу деформациясы жиі кездеседі.Басты өстерге қатысты инерция моменттері өзара тең болғанда,қиғаш иілу болмайды,осыған байланысты қимасы дөңгелек білеулер-қиғаш иілмейді.Сондықтан,қимасы дөңгелек білеулер иіліп,созылып,сығылып,бұралады.

Көлденең қимасында бойлық күш болмайтын білеу,иіліп бұралу деформациясына жұмыс істейді.Оның қауіпті нүктесін анықтау үшін,білеу бойымен ию моменті мен бұру моменті қалай өзгеретінін білген жөн,яғни олардың эпюраларын тұрғызу керек.Ең үлкен ию моменті әсер ететін қимада,ең үлкен бұрау моменті әсер етсе,бұл қима қауіпті болып есептеледі.Ең үлкен ию моменті мен ең үлкен бұрау моменті әсер ететін қималар сәйкес келмесе, қауіпті қима,олардың ең үлкен мәндеріне сәйкес келмейтін қима болуы мүмкін.Ию моменті мен бұрау моменті арқылы,қауіпті қима анықталмаса,беріктікті бірнеше қимада тексеріп,қауіпті кернеу анықталады.

Тік кернеу σ=

Жанама кернеулердің ең үлкен мәні τ=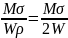

Мұндағы W-қиманың өстік қарсыласу моменті, W𝛒=2W-полярлық қарсыласу моменті.

Пара-педтің беттерінде σ= тік ж/е τ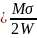 жанама кернеулер әсер етеді.Жанама кернеулердің жұптық заңы б/ша пара-педтің жоғарғы ж/е төменгі беттерінде де жанама τ кернеуі пайда болады.

Басты кернеулер белгілі формуладан анықталады

σ_max/min= (1)

Иіліп бұралған білеу ,пластикалық материалдан жасалса,үшінші н/е төртінші беріктік теориясы,ал морт материалдан жасалса МОР теориясы б/ша есептеледі.

үшінші беріктік теориясы σ₁-σ₃≤[σ]н/е (1) –нен

(2)

Қианың қауіпті нүктесіндегі кернеуледің өрнектерін пайдалансақ

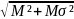- үшінші беріктік теориясы б/ша келтірілген момент.

Төртінші беріктік теориясы б/ша

Басты кернеулердің мәнін ескерсек

45. Серпімді жүйелердің тепе-тендік күйінің орнықтылығы. Аумалы күш. Эйлер формуласы.

Теориялық механикадан, қатты денелердің тепе-теңдік күйі орнықты немесе орнықсыз болады.Ойыс сфераның түбінде орналасқан шариктың тепе-теңдік күйі орнықты (28.1а-сурет),ал дөңес сфераның төбесінде орналасқан шариктың тепе-теңдік күйі орнықсыз (28.1б-сурет).Серпімді жүйелердің статикасында тепе-теңдік күйдің орнықты,орнықсыз жағдайлары кездеседі.

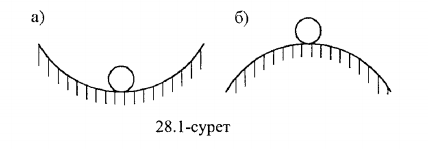
Серпімді жүйенің тепе-теңдік күйінің орнықтылығы,оның өлшемдеріне,материалдарына,әсер етуши күштердің шамасы мен бағыттарына тәуелді.Мысалы (28.2а-сурет)сығылған сырықтың тепе-теңдік күйі күштің аз шамасында орнықты болса,ал ол белгілі бір шеткі мәнінен асқанда орнықсыз күйге көшеді.

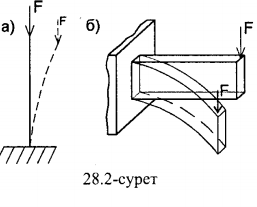
Аумалы күш. Эйлер формуласы.

Аумалы кернеуді анықтау үшін ,шамалы майысқан сығылған сырықты тепе-теңдік күйде ұстап тұратын шамасы ең аз өстік немесе аумалы күшті табу.

Екі ұшы топсалы бекітілген,қималары түзу сырықты қарастырамыз.Сырықты күшімен жүктеп қатаңдығы аз жазықтықта шамалы майыстырамыз. болғандықтан сырық майысөан күйін сақтайды.Сырықтың иілу деформациясы өте аз болғандықтан ,иілген остің жуықталған дифференциалдық теңдеуін қолданамыз. А нүктесін координата бас нүктесі ретінде қабылдап,өстердің бағыты 28.3-суретте көрсетілген.

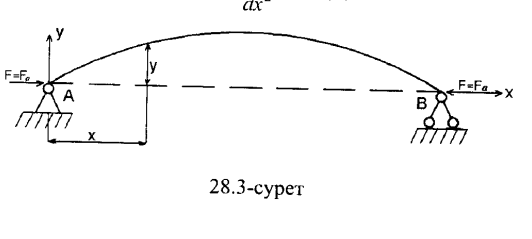
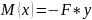
Бұл теңдеудің жалпы интегралы

Теориялық тұрғыдан,шамалы майысқан сырықты тепе-теңдік күйде ұстап тұратын күштің саны оте аз.Іс жүзінде бізге қажеттісі осылардың ішіндегі шамасы ең аз n=0 болғанда есептің шартын қанағаттандырылмайды,сондықтан n=1 болғанда

n=2,3 болғанда

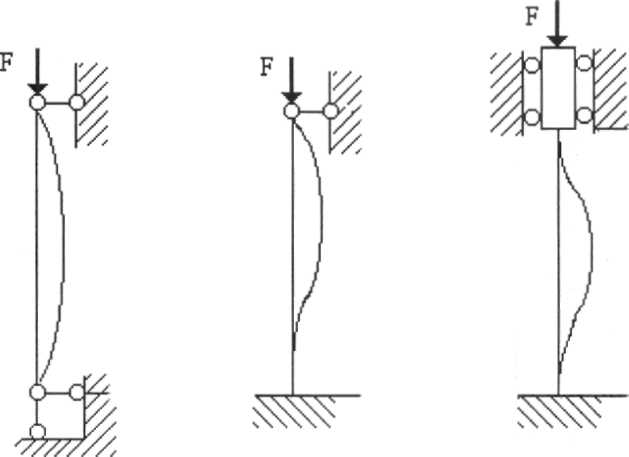
n=1 n=2 n=3

Аумалы кернеу сырық ұзындығының кіші инерция радиусына қатынасының квадратына кері пропорционал, бұл қатынас сырықтың иілгіштігі.