39. Ию моменті, қолденең күш, таралған күш қарқындылығы арасындағы дифференциалдық байланыс.

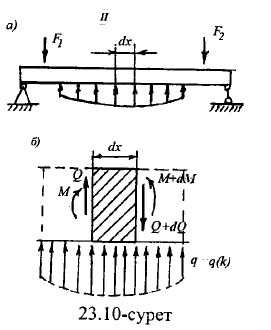Жазық күштер жүйесі әсер ететін арқалықты қарастырайық. Арқалықтан бөлінген ұзындығы өте кішкентай dx қарапайым элемент қарқындылығы q таралған күштің және Q,

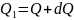
Көлденең күштер мен М, 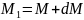ию моменттерінің әсерінен тепе-теңдік күйде болды. Бөлінген элементтің тепе-теңдік теңдеулері келесі түрде жазылады:

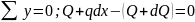
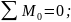
M+Qdx+qdx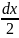 –(M+dM)=0

Бірінші теңдеуден qdx-dQ=0

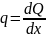
Көлденең күштің қима абциссасы бойынша, бірінші туындысы таралған күштің қарқындылығына тең. Екінші теңдеуден, екінші реттіаз шамаларды ескрмей

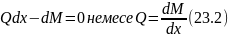
Ию моментінің қима абциссасы бойынша бірінші туындысы көлденең күшке тең.

23.2 екі жағынан х бойынша туынды алсақ

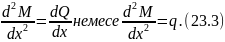
23.3 формуласы Журавский теоремасы деп аталады.

Ию моментінің қиманың абциссасы бойынша екінші туындысы таралған күштің қарқындылығына тең. Егер q төмен бағытталса 23.3

23.2 23.3 формулаларынан

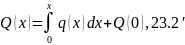
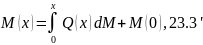
Мұндағы Q(0),M(0) тұрақтылары аралық басындағы қадалған күш пен ию моменті. 23.2 өрнегінен таралған күш қарқындылығы q=0 қимада көлденең

күш Q эпюрасына жанама, арқалық осьіне параллель. Осы сияқты 23.3-ден 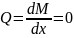қимасында ию моменті ең үлкен немесе ең кіші мәніне ие болады.

40)Таза иілу.

Иілу кезінде арқалықтың көлденең қимасында июші момент пен көлденең күш пайда болады. Кернеулі күйді зерттеу кезінде дербес жағдайда көлденең күш Q=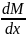 =0; тең болатын таза иілуден бастау тиімді. Егерде иіуші момент қимаға әсер ететін жалғыз ғана күш әсері болса, онда иілу таза иілу деп аталады. Арқалықтың жеке салмағын елемегенде орта бөлігінде (төмендегі суретте көрсетілген )таза иілу пайда болады.

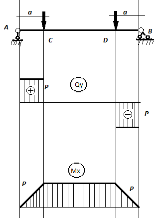
Таза иілуде арқалықтың меншікті салмағы ескерілмейді.Тза иілуде арқалықтың қимасындағы ішкі күштер сол қимадағы ию моменттерін теңестіретін қос күшке тең болуы тиіс.Мұндай қос күштер тек тік кернеудің әсерінен туады себебіолар ию моменті жататын арқалықтың симетриялы жазықтығына паралель.Тік кернеулерден тек қос күш пайда болу үшін,олардың ішінде оң таңбалысымен қатар, теріс таңбалыларда болуы тиіс , сондықтан қимасының биіктігі бойымен арқалық талшықтары созылады және сығылады.Айтылған талшықтардың арасында не созылмайтын не сығылмайтын бір талшық кездеседі.Оны бейтарап талшық дейді.Осындай талшықтардын тұратын жазықтық бейтарап жазықтық д.а. Бейтарап жазықтықпен арқалықтың көлденең қималарының қиылысу сызығы бейтарап өс немесе бейтарап сызық д.а. 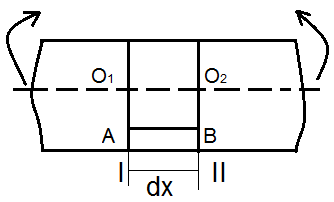Деформацияға деиін арқалықтың жазық көлденең қимасы деформациядан кеиінде жазық күйін сақтайды, тек бейтарап өстің айналасында бұрылады.Таза иілгенде арқалықтың кез-келген бойлық елементі , бойлық талшықтары тек өсі бойымен созылады не сығылады , ал кез-келген горизанталь ауданшада кернеу болмайды , сондықтан көрші талшықтар бір-біріне қысым көрсетпейді.Иілу деформациясы серпімділік шектен асапағанда бойлық талшықтар бір-біріне қысым жасамайтындығы ескеріліп Гук заңынан қарапайым созылудағы кернеу анықталады.σ=εE=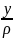 E; 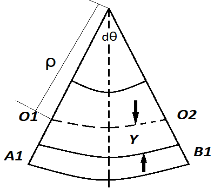Бөлініп алынған элемент үшін қисықтық радиусы ρ тұрақта болғандықтан иілудегі кернеу қима биіктігі бойынша бейтарап өске дейінгі ара қашықтыққа тура пропорциянал заңдылықпен өзгереді.Кернеудің ең үлкен мәндері бейтарап өстердің бойында 0-ге тең. Талшықтың салыстырмалы ұзаруы ε=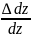 = ;болады.у-бейтарап өске деиінгі ара қашықтық. 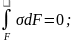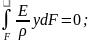Бейтарап остің орны белгісіз болғандықтан кернуді (σ) анықтауға мүмкіндік жок.Ол үшін y қашықтықтағы бейтарап сызықтың орнын анықтаймыз.Ол үшін таза иілу кезіндегі σdF элементар тік күштердің қосындысы көлденең қимада 0-ге тең екендігін пайдаланамыз.N= немесе 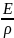көбейткіші 0-ге тең болмайтындықтан, оны интегралдап қысқартсақ онда 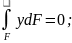бұл ОХ бецтарап өсіне қатысты көлденең қима ауданының статикалық моментін көрсетеді.ол өс арқалықтың қиманың ауырлық центрнен откенде ғана –ге тең олай болса иілу кезінде тік арқалықтың бейтарап өсі қиманың бейтарап өсінен өтеді.Енді бейтарап өске қатысты ішкі күштер моменттерін табайық.Ол үшін өске қатысты 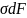ішкі күштер моментерінің қосындысын есептеп оны июші моментке теңестіреміз. М_х=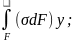 σ орынына өзінің мәнін қойсақ онда М_х=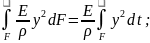 Өрнекке кірітін интеграл стержіннің көлденең қимасының инерция моментін бейнелейді.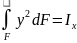 ; сондықтан 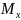= 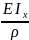; осыдан бейтарап қабаттың қисқтығын табамыз. 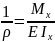; бастапқы формулаға қойсақ σ= 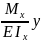соңғы формула арқалаықтың көлденең қимасының бейтарап осінен y қашықтықта горизанталь сызығында жатқан кез келген нүктедегі кернеуді анықтауға мүмкіндік береді. Формуладана кернеу у шамасына сызықты байланыста екендігі көрінеді.Қиманың биітігі бойынша кернеулердің өзгерісін көрсететін график кернеу епюрі д.а. Ең үлкен кернеу нүктеде у шамасының ең үлкен мәнінде, яғни ең шеткі талшықта болады.