25. Қатты дененің кинетикалық энергиясы.

Қатты дененің кинетикалық энергиясы деп жүйе құрамына енетін барлық нүктелердің кинетикалық энергиясының арифметикалық қосындысына тең скалярлық шаманы айтады.

Ілгерілемелі қозғалыстағы дененің кинетикалық энергиясы дене массасы мен оның массалар центрі жылдамдық квадратттары көбейтіндісінің жартысына тең.

Айналмалы қозғалыстағы дененің кинетикалық энергиясы дененің айналу өсіне қатысты инерция моменті мен оның бұрыштық жылдамдық квадраттары көбейтіндісінің жартысына тең.

Қатты дененің жазық параллель қозғалыстағы кинетикалық энергиясы дененің барлық массасы шоғырланған деп ұйғаруға болатын массалар центрінің ілгерілемелі қозғалыстағы кинетикалық энергиясы мен дененің массалар центрі арқылы қозғалмайтын жазықтыққа перпендикуляр жүргізілген өстен айналмалы қозғалысының кинетикалық энергиясының қосындысына тең

26.Қиманың статикалық моменті.Қималардың инерция моменті.Параллель осьтерге қатысты инерция моменті.

1.Қандайда бір х осьне қатысты қиманың статикалық моменті деп,келесі интеграл арқылы анықталатын геометриялық сипаттаманы айтады.

S= (1)

Мұндағы у қарапайым dA ауданшадан х осьне дейінгі ара қашықтық.

Статикалық моменттің өлшем бірлігі ұзындықтың үшінші дәрежесі (cm³) ж/е оның мәні оң,теріс,нөлге де тең болуы мүмкін.

(2)

Мұндағы А-қиманың толық ауданы (тең әсер), -қиманың ауырлық орталығынан х өсіне дейінгі ара қашықтық.

у өсіне қатысты статикалық момент

(3)

(2),(3) өрнектері негізінде

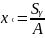, = (4)

Қиманың ауырлық орталығын анықтау формуласы.

Егер х,у өстері қиманың ауырлық орталығы арқылы өтетін болса, онда статикалық момент нөлге тең.Мұндай өстер орталық өстер деп аталады.

Көптеген жағдайларда (2),(3) қарапайым интегралдың орнына қос интегралды пайдаланған ыңғайлы,яғни

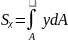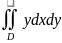= (5)

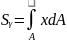= (6)

Мұндағы D интегралдау облысы.

2.Қиманың х н/е у өстеріне қатысты инерция моменті деп,келесі интегралдар арқылы анықталатын геометриялық сипаттамаларды айтады.

Iᵪ= , Iᵧ= (7)

Полярлық инерция моменті,келесі интегралмен анықталатын геометриялық шама

I_𝛒= (8)

Ортадан тепкіш инерция моменті деп келесі геометриялық сипаттаманы айтады.

Iᵪᵧ=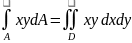 (9)

Ортадан тепкіш инерция моменті оң,теріс таңбалы ж/е нөлге тең болуы мүмкін.

Өзара перпендикуляр х,у өстерінің кем дегенде біреуі,қиманың симметрияы өсі болса,онда бұл өстерге қатысты ортадан тепкіш инерция моменті нөлге тең.Нүктеге қатысты полярлық инерция моменті,осы нукте арқылы өтетін өзара перпендикуляр х,у өстеріне қатысты инерция моменттерінің қосындысына тең,

х²+у²=𝛒² сондықтан I_𝛒= Iᵪ+ Iᵧ

3. Қималардың геометриялық сипаттамаларын,әр түрлі орналасқан өстерге қатысты есептеуге тура келеді.Белгілі х,у өстеріне қатысты инерция моменттері (I_х,I_у,I_ху) анықталған.Алғашқы өстерге параллель х₁,у₁ өстеріне қатысты,инерция моментін анықтайық.Жаңа координаталық жүйеде қрапайым ауданшаға дейінгі ара қашықтықтар у₁=y+a, x₁=x+b өстік инерция моменттерін анықтау формуласын ескерсек

I_x1= (10)

Мұндағы 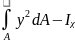инерция моменті, статикалық момент ,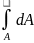

Қиманың ауданы А,сонымен

I_x1=I_x+2aS_x+a²A (11)

y₁ өсіне қатысты инерция момент (11) сияқты,келесі түрде жазылады.

I_y1=I_y+2bS_y+b²A (12)

х,у өстері ауырлық орталық арқылы өткенде ,

I_x1=I_x+a²A. I_y1=I_y+b²A (13)

Кез келген өске қатысты инерция моменті,осы өске параллель,орталық өске қатысты инерция моментіне қиманың ауданы,өстердің ара қашықтықтарының квадратына көбейтіп,қосқанға тең.Ауырлық орталық арқылы өтпейтін кез-келген өске қатысты,инерция моменті орталық өске қатысты инерция моментінен үлкен,себебі а²А,b²A оң таңбалы шамалар .

I_x1y1=I_xy+bS_x+abA

Жеке жағдайда х,у өстері ауырлық орталық арқылы өтсе

I_x1y1=I_xy+abA (14)

Симметриялы қима үшін х,у өстерінің біреуі симметрия өспен сәйкес келсе I_x1y1=abA