23)Механикалық жүйе туралы ұғым.Әсер ететін күштер.

Материялық нүктелер жиынтығынан тұратын кез келген денені механикалық жүйе деп қарастыруға болады.Механикалық жүйені құрайтын нүктелердің орны мен қозғалысы басқа нүктелер орны мен қозғалыстарына тәуелді.

Материялық нүктелер жүйесінің мысалы ретінде планеталары материялық нүктелер деп қарастырылатын күн жүйесін алуға болады.Абсолют қатты дене өзгермейтін механикалық жүйе ретінде қарастырылады.Материялық нүктелер арақашықтығы өзгеріп отыратын механикалық жүйені өзгермелі жүйе деп атайды.Олардың қатарына кез келген машиналар мен мханизм жатады.Динамика есептерін шығарған кезде механикалық жүйе нүктелеріне әсер ететін күштерді сыртқы және ішкі күштер деп бөлу тиімді болады.

Сыртқы күштер деп осы механикалық жүйе құрамына енбейтін нүктелер денелердің жүйе нүктелеріне әсер ететін күштерін айтамыз.Бұл күштер байланыс реакцияларына тәуелсіз болғандықтан,кейде актив күштер деп атаймыз.

Ішкі күштер деп механикалық жүйе нүктелерінің немесе берілген жүйе денелерінің өзара бір бірімен әсерлесу күштерін айтады.Механикалық жүйе қозғалысы әсер ететін күштерге ғана емес жүйенің массасына және массалар центрінің орнына тәуелді.Жүйе массасы жүйе құрамына енетін нүктелер немесе дене массаларының арифметиалық қосындысына тең.

Мұндағы М-жүйе массасы.Егер механикалық жүйе Жердің тартылыс өрісінде орналасса,онда массалар центрінің орны жүйенің ауырлық центрінің орнымен дәлме дәл келеді.Массалар центрі және ауырлық центрі деген ұғымдарды бірдей деп қарастыруға болмайды.Жүйе құрамындағы массалар таралымын сипаттайтын массалар центрі орны,жүйе күш әсерінде бола жоқ алде болмайма деген ұғымға тәуелсіз.Былай айтқанда егер механикалық жүйені Жердің тартылыс өрісінен алып кетсе,ауырлық центрі деген ұғым өзінің мағынасын жоғалтады,ал массалар центрі өзінің орны мен мағынасын сақтап қалады.

24.Дененің тұрақты өстен айналмалы қозғалысының теңдеуі. Біртекті денелердің инерция моменттерін есептеуге арналған мысалдар.

Даламбер принципі бойынша қатты денеге әсер ететін актив күштер, реакция күштері және инерция күштері теңескен күштер жүйесін құрайды, яғни осы күштердің айналу өсіне қатсты моментерінің алгебралық қосындысы нөлге тең болуы қажет.

- денеге әсер ететін сыртқы күштердің айналу өсіне қатысты моменттерінің қосындыы жіне ол айналдырушы момент деп аталады.

Онда

Дененің барлық нүктелерінің массалары мен олардың айналу өсінен қашықтықтықтар квадраттары көбейтінділерінің қосындысына тең болатын – өрнегі дененің z өсіне қатысты инерция моменті деп аталады және деп белгіленеді.

Осының нәтжесінде алатынымыз

Соңғы өрнек дененің айналмалы қозғалысының негізгі немесе дифференциалдық теңдеуі деп аталады.

Инерция моментінің СИ жүйесіндегі өлшемі

Біртекті денелердің инерция моменттерін есептеуге арналған мысал.

Массасы М радиусы R біртекті дискі немесе цилиндрдің массалар центрі арқылы диск (цилиндр) жазықтығына перпендикуляр өтетін Cx өсіне қатысты инерция моменті.(сурет)

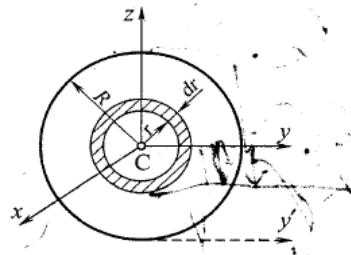Алдымен, радиусы r, ені dr элементар сақинаны юөліп алайық. Осы сақинаның ауданы , массасы