1.Статика аксиомалар. Үш күш туралы теорема. Байланыстар. Байланыстар реакциясы. Статика негізіне адамзаттың ғасырлар бойы жиған тәжірибесінің нәтижесінде түжырымдалып, математикалық дәлелдеуді қажет етпейтін аксиомаға айналған заңдылықтар жатады.Осы аксиомалар статикада қарастырылатын барлық мәселелерді қорытып шығаруға әбден жеткілікті.

Бірінші аксиома- өзара теңескен күштер жүйесінің әсерінен,дене тыныштық күйде немесе бірқалыпты түзу сызықты қозғалыста болады.Галилей тұжырымдаған бұл аксиома инерция принципі деп аталды,өйткені материялық нүктенің күш әсерінсіз түзу сызықты және бір қалыпты қозғалысы инерциялық қозғалыс болады.

Екінші аксиома.(екі күштің тепе- теңдік шарты туралы).Сан мәндері тең ,бір түзудің бойымен қарама- қарсы бағытталған еркін қатты денеге әсер етуші екі күш,өзара теңеседі немесе нөлге баламалы.Ғ1=-Ғ2 .(Ғ1,Ғ2)=0.

Үшінші аксиома.Өзара теңескен күштер жүйесін қосқанан немесе алып тастағаннан берілген күштер жүйесінің қатты денеге әсері өзгермейді.

Төртінші аксиома.(Күштер параллелограмының заңы).Дененің бір нүктесіне түсірілген екі Ғ1 және Ғ2 күштерінің тең әсер етуші күші сол нүктеге түсіріледі де,осы күштерден тұрғызылған параллелограмның диоганалымен анықталады.Векторларды қосу ережесі бойынша тең әсер етуші күш R=F1+F2; яғни күштердің векторлық немесе геометрикалық қосындысына тең.Тең әсер етуші күштің модулі косинустар теоремасы бойынша R=(F₁²+F₂²+2*F₁F₂cos(F₁F₂) )^1/2 .Бесінші аксиома.(әсер және кері туралы заң).Екі дененің бір-біріне әсер ету күштері шамасы жағынан тең және бір түзу бойымен қарама-қарсы бағытталады.F_A=-F_B;

Алтыншы аксиома.(қатаю принципі).Егер қатты емес дене тепе-теңдікте болса,онда ол қатты денеге айналғанда тепе –теңдік шарты бұзылмайды.

Үш күш туралы теорема. Егер бір-біріне паралель емес ,бір жазықтықта орналасқан үш күштің әсерінен дене тепе-теңдікте болса,онда күштердің әсер ету сызықтары бір нүктеде қиылысады.

Байланыстар.Байланыстар реакциясы.статиканың барлық заңдылықтары мен теоремалары тек еркін қатты дене үшін орынды.Барлық денелер еркін және еріксіз болып бөлінеді.барлық бағыттарда қозғала алатын дене еркін ал кеңістікте басқа бір немесе бірнеше денемен шектелсе еріксіз болады.Дененің орын ауыстыруын шектейтін шарттарды механикада байланыстар д.а.Осы шектеу кезінде дене тепе-теңдікте б/са,оның байланысқа әсері 5-аксиома бойынша қарсы әсер туғызады.Осы байланыс тарапынан қарсы әсер болатын күші байланыстың реакция күші немсе байланыс реакциясы д.а.

Байланыстар аксиомасы.(байланыстан босану принципі ) Кез келген еріксіз денені ойша байланыстардан босатып және осы байланыстар әсерін сәйкес реакция күштерімен алмастырсақ , онда еріксіз денені еркін дене деп қарастыруға болады.

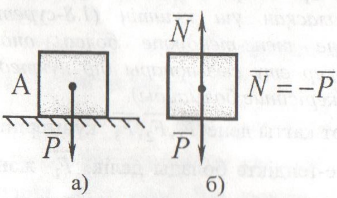
Денелдің өзара түйісуі .мұндай байланыс дене қрзғалысын жанасушы беттерге жургізілген ортақ нормаль бағытында шектейді.сондықтан жылтыр беттің жанасушы беттерге ортақ нормаль бойымен бағытталады және осы реакция күшін нормаль реакция күші д.а.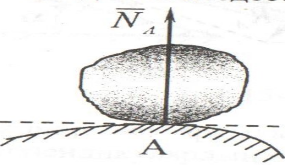

Иілгіш (керілгіш) байланыстар(жіп,арқан, шынжыр т.б).Созылмайтын иілгіш жіп ,арқан түрінде берілген байланыстар дененің бір бағыттағы (созылу,керілу бағыты)қозғалысын шектейді.Сондықтан байланыстың бұл түрінің реакциясын сол байланыстың боймен бағытталады.

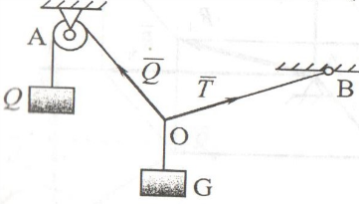
Денелерді жылжымайтын цилиндірлік шарнирмен (подшипникпен )байланыстыру.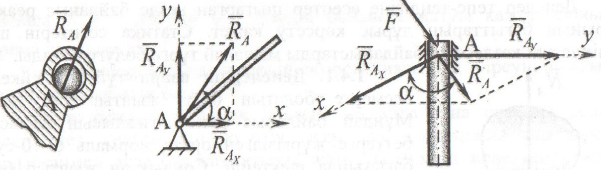

Денелердің жылжымайтын сфералық шарнирмен байланыстыру.

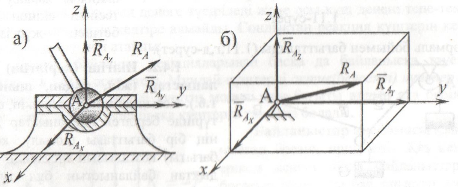
Денелерді жылжымалы шарнир (каток)арқылы байланыстыру.

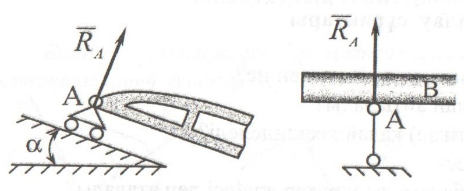
Қатаң бекітіліс.

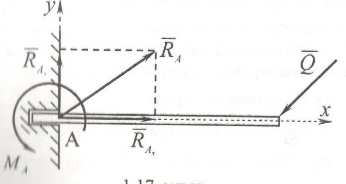
2.Жинақталатын күштер жүесінің тең әсер етуші күшін анықтаудың геометриялық және аналитикалық тәсілі.

Әсер ету сызықтары бір нүктеде қиылысатын күштер жиынтығы жинақталатын күштер жүйесін құрайды.

Егер А₁,А₂,,,,,A_n нүктелеріне түсірілген (2.1а-сурет)жинақталатын кеңістік күштер жүйесінің F₁,F₂,,,,,F_n (F вектор) күштерін,әсер ету сызықтарының бойымен О нүктесіне көшірсек (2.1б-сурет)

3 аксиомадан шығатын салдар бойынша осы күштер жүйесінің абсолют қатты денеге әсері өзгермейді.Сонымен кез келген,жинақталатын күштер жүйесін бір нүктеде түсірілетін баламалы күштер жүйесімен алмастыруға болады.

Абсолют қатты дененің А нүктесінде әсер ету сызықтары бір жазықтықта жатпайтын саны төртке тең F₁,F₂ ,F₃,F₄ (F вектор) күштері әсер етеді делік (2,2 а-сурет).Осы күштер жүйесінің тең әсер етуші күшін анықтайық.Бір нүктеде қиылысатын екі күш үшін төртінші аксиомада тұжырымдалған күштер үшбұрышы ережесін қолдана отырып алдымен F₁ және F₂ күштерін қосамыз.Ол үшін F₁ векторының ұшынан F₂ күшіне тең ВС векторын жүргіземіз. F₁ және F₂ күштерінің тең әсер етуші күші R_1,2 алынған масштабта үшбұрыштың тұйықтаушы АС қабырғасымен,демек АС векторымен бейнеледі,яғни R_1,2=. F₁+ F₂ (R_{1,2 ,}F-вектор)

Одан кейін осы ережені қолдана отырып, R_1,2 және F₃ күштерінің тең әсер етуші күшін табамыз.

R_1,2,3= R_1,2 + F₃ (R_{1,2,3 ,}F-вектор)

R_1,2,3 күші үш күшке балама.Онан әрі осы ережені қолдана отырып төрт күшке балама болатын тең әсер етуші күшті табамыз.Егер күштер жүйесі n санды күштерден құрылса осынай әдіспен барлық күштер жүйесіне балама болатын тең әсер етушіні аламыз.

R=R_n-1+F₄=F₁+F₂+,,,,+F_n (R,F векторлар)

Сонымен, R (вектор )күші берілген жинақталатын күштер жүйесі үшін тең әсер етуші күш болады

Қатты денеге n санды (F₁,F₂,,,F_n векторлары ) жинақталатын күштер жүйесі әсер ететін болсын делік.Осы күштер жүйесінің тең етушісі (R,F_k вектор)

Координаталар өстерін жүргізіп берілген күштердің және олардың тең әсер етушісінің осы өстерге проекцияларын анықтайық.

Математикадан векторлық қосындысын қасиеті бойынша тең әсер етуші вектордың кез келген өске проекциясы құраушы векторлардың сол өске проекциядарының алгебралық қосындысына тең.Онда тең әсер етуші күштің координат өстеріне проекциялары

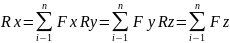(2.3)

Тең әсер етуші күштің R_x R_y R_z проекцияларын параллелипедтің қабырғалары ретінде қарастырып болсақ,онда оның диагоналы болып саналатын тең әсер етуші күштің модулі,

R= R_x²+R_y²+R_z²=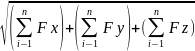 квадраттарынын косындысы (2.4)

Тең әсер етуші күштің x,y,z өстерімен жасайтын бұрыштары бағыттаушы косинустармен анықталады.

Cos(R^i)=R_x/R; Cos(R^j)=R_y/R; Cos(R^k)=R_z/R; (2.5)

(2.4) және (2.5) формулалары жинақталатын кеңістіктік күштер жүйесінің тең әсер етуші күшінің шамасы мен бағытының аналитикалық түрде анықтамасын береді.

3.Жинақталатын күштер жүесінің тепе-тендік шарты мен теңдеулері. Статика есептерін шешудің жалпы әдісі.

Тепе-теңдік шартының геометриялық түрі. Абсолют қатты денеге әсер ететін жинақталатын күштер жүйесінің тең әсер етуші күші нөлге тең болса, дене өзінің тыныштық не қозғалыстағы күйін өзгерте алмайды. Осы жағдайда әсер етуші күштерден құрылған күштер көпбұрышы тұйықталынады және бірінші 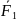күшінің бастапқы түсу нүктесі мен соңғы 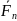векторының ұшы бір-біріне дәл келеді. Сондықтан геометриялық тұрғыдан қарастырғанда абсолют қатты денеге әсер ететін жинақталатын күштер жүйесі тепе-еңдікте болу үшін, осы күштерден құрылған көпбұрыш тұйық болуы қажетті және жеткілікті.

R=0. (2.6)

Тепе-теңдік шартының аналитикалық түрі. Жинақталатын күштер жүйесі тепе-теңдікте болған жағдайда (2.4) теңдеуінің түбір астындағы тең әсер етуші күштің сәйкес өстерге проекциялары да нөлге тең болады, яғни 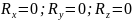Олай болса

Сонымен, кеңістіктегі жинақталатын күштер жүйесі тепе-теңдікте болуы үшін барлық күштердің әрбір координат өстеріне проекцияларының алгебралық қосындысы нөлге тең болуы қажет және жеткілікті.

Жазықтықта орналасқан жинақталатын күштер жүйесінің тепе-теңдік теңдеулері:

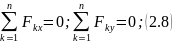
Статика есептерін шешу кезінде тепе-теңдікте болатын еріксіз денеге түсірілген актив (белсенді) күштердің шамалары мен бағыттарын белгілі деп ала отырып белгісіз байланыс реакция күштерін анықтайды. Бұл жағдайда осы денеге түсірілген белсенді күштер мен реакци күштері тепе-теңдікте болатын күштер жүйесін құрайды.

Есепті аналитикалық әдіспен шығарғанда күштер жүйесінің тепе-теңдік теңдеулерін жазып, белгісіз күштерді осы теңдеулер жүйесін шешу арқылы табамыз. Осы теңдеуле Белгісіз реакция күштерін табу үшін қолданылады. Егер белгісіз күштер саны осы есепке сәйкес жазылатын тепе-теңдік теңдеулер санынан көп болмаса, онда мұндай есептер статикалық анықталған есептер қатарына жатады.

Егер белгісіз күштер саны осы есепке сәйкес жазылатын тепе-теңдік теңдеулер санынан артық болса, онда мұндай есептер статикалық анықталмаған есептер деп аталады.

Егер тепе-теңдікте қаралып отырған конструкция өзара байланысқан бірнеше бөліктерден тұратын болса, онда осы бөліктерді бір-бірінен ажыратып, әрқайсысы үшін тепе-теңдік теңдеулерін жазуға болады. Осындай әдісті қолданудың нәтижесінде белгісіз шамалар мен теңдеулер саны теңестіріледі де, статика есептері ретінде анықталмайтын құрылым анықталатын құрылымға айналады.

Статика есептерін шешудің жалпы әдісі.

Статика есептерін шешу кезінде төмендегідей ережені қолдану ұсынылады.

1. Тепе-теңдігі қарастырылатын денені немесе нүктені айқындап алу.

2. Денеге түсірілген актив күштермен қатар, оның қозғалысын шектеп тұрған байланыстардың реакциясын көрсету.

3. Денеге әсер ететін күштер жүйесінің түрін анықтау, үш күштер тепе-теңдігі туралы теореманы қолданудың мүмкіншілігін ескеру.

4. Белгілі бір әдістің (графикалық, геометриялық, аналитикалық) шарттары мен тепе-теңдік теңдеулерін пайдаланып белгісіз шамаларды анықтау, есептеу нәтижелерін талдау.