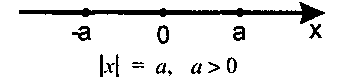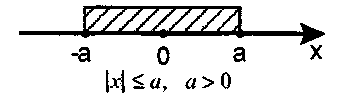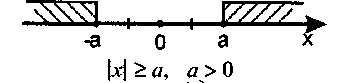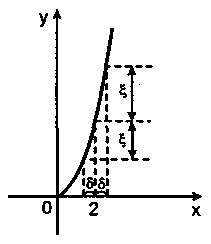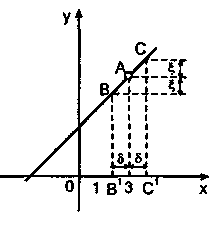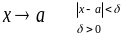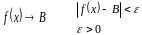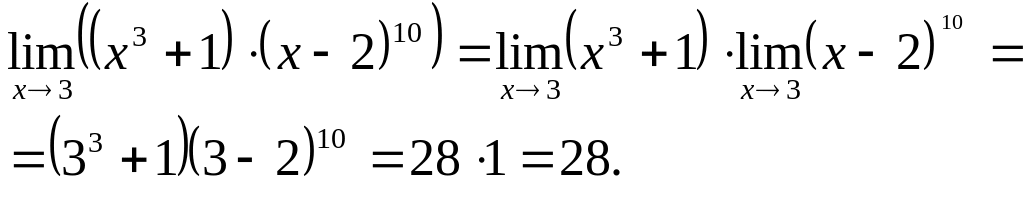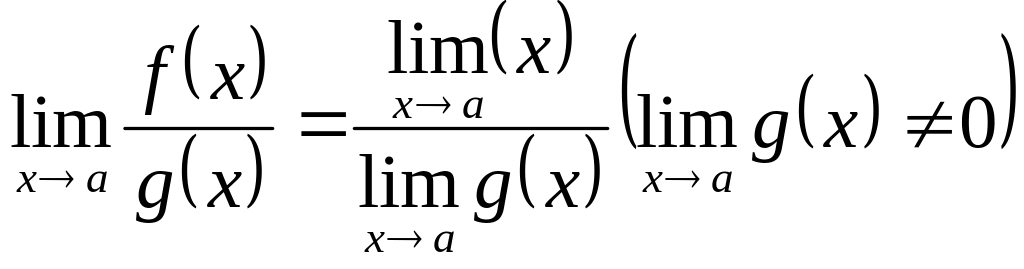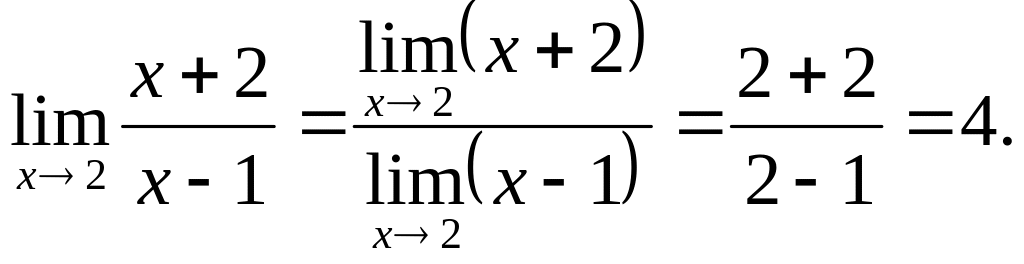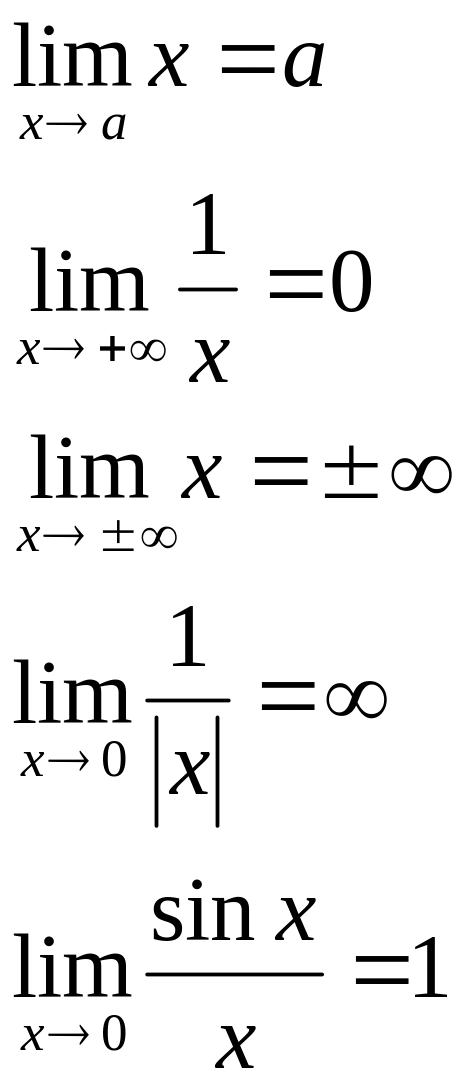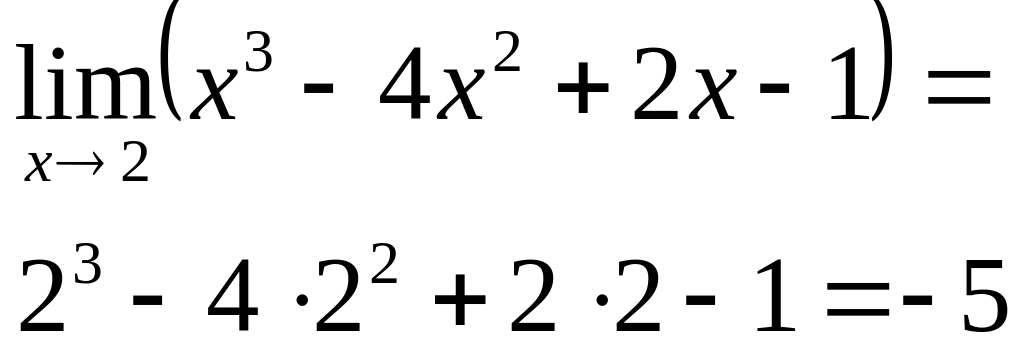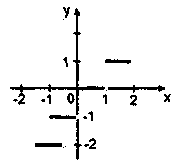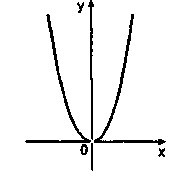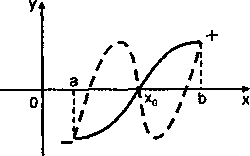Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ровенский государственный гуманитарный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

30 (2).doc

Скачиваний:

Добавлен:

01.07.2025

Размер:

1.33 Mб

Скачать

☆

1 / 31 2 3 > Следующая >>>

Модуль числа.

Модуль додатного числа дорівнює самому числу.

Модуль від’ємного числа є число йому протилежне.

Модуль нуля дорівнює 0.

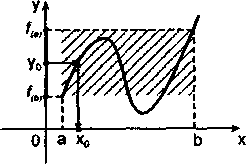
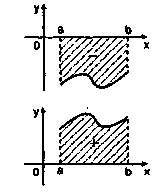
Геометричний зміст модуля

Приклади, в яких демонструється геометричний зміст модуля числа

бо

бо .

Розв’язування рівнянь, які містять знак модуля

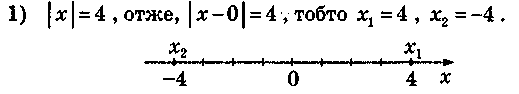
Відповідь:-4;4.

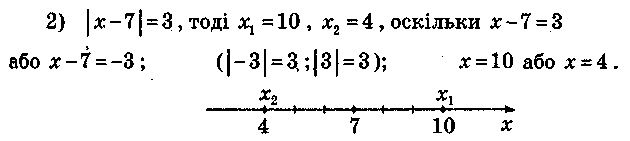
Відповідь:4;10.

3) , отже, . Геометрично це означає, що шукані числа розташовані на відстані 8 одиниць ліворуч і праворуч від числа -5. x₁=-5+8=3; x₂=-5-8=-13.

Інакше можна записати: або , тоді або ;

або .

Відповідь: -13;3.

Розв’язування нерівностей, які містять знак модуля

— окіл точки 

Якщо з точністю, більшою ніж 0,01, то записують .

Точність більша, ніж 0,01, отже, число таке, що

1) Нерівність геометрично означає, що точки на числовій прямій розташовані від точки 4 на відстані, не більшій за 5 одиниць.

Відповідь: [-1;9].

2) Нерівність геометрично означає, що точки на числовій прямій розташовані від точки 2 на відстані, не меншій за 3 одиниці.

або ;

або .

Відповідь:

Розв’язування рівнянь з модулем

1) Рівняння виду рівносильне сукупності рівнянь або .

Інакше можна записати:

Приклад. Розв’яжіть рівняння .

Розв’язання

або ,

або

Відповідь: -11; .

2) Рівняння виду рівносильне сукупності двох систем:

або

Інакше можна записати:

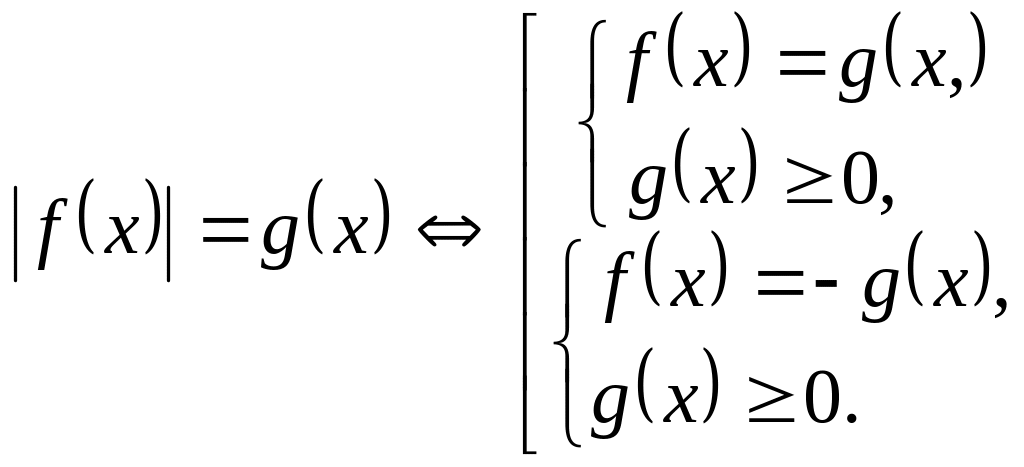
Приклад. Розв’яжіть рівняння ²- 4x =-x

Розв’язання

або

Відповідь:0.

Розв’язування нерівностей з модулем

1). Нерівність виду рівносильна системі або подвійній нерівності .

Приклад Розв’яжіть нерівність .

Розв’язання

Відповідь: .

2). Нерівність виду рівносильна сукупності двох нерівностей:

f(x) g(x) або f(x) -g(x).

Приклад. Розв’яжіть нерівність

Розв’язання

або ,

або .

Відповідь: .

3). Нерівність виду рівносильна нерівності .

Приклад. Розв’яжіть нерівність .

Розв’язання

Відповідь:

Границя функції. Поняття функції.

Приклад 1.

Розглянемо таблицю значень функції в точках, які на числовій прямій розташовані досить близько до числа 2 (і в самій точці 2).

1,98	1,99	2,00	2,01	2,02
3,92	3,96	4,00	4,04	4,08
0,08	0,04	0	0,04	0,08

Чим ближче аргумент до числа2 (пишуть ), тим ближче значення функції до числа 4 .

Записують так:

Приклад 2.

Розглянемо таблицю значень функції поблизу точки .

2,96	2,98	3	3,02	3,04
5,96	5,98	не визначено	6,02	6,04
0,04	0,02		0,02	0,04

Якщо .

В загальному випадку означає: якщо .

Число називається границею функції при , що прямує до , якщо для будь якого додатного числа знайдеться таке додатне число , що при всіх , які задовольняють нерівність , виконується нерівність: .

Якщо — єдина.

Теореми про границі.

Теореми про границі	Приклади

Якщо , то .

Якщо і

, то .

Способи обчислення границь.

Для будь-якого многочлена : .
2. Якщо число входить до області визначення дробово-раціональної функції , то	.
Якщо в результаті підстановки одержали вираз то:
а) спробуємо розкласти чисельник та знаменник на множники і скоротити дріб;	1) ; 2) ; 3) .
б) Якщо дріб не можна скоротити, то в цьому випадку слід чисельник та знаменник дробу домножити на вираз, спряжений із знаменником (або чисельником), а потім скоротити дріб;	;
в) якщо під знаком границі стоять тригонометричні функції або обернені тригонометричні функції, то зводимо до першої визначної границі якщо	1) ; 2) ;

Неперервність функції

Функція називається неперервною в точці , якщо вона в ній визначена, границя функції в точці існує і дорівнює значенню функції в цій точці.

За цим означенням ставляться три вимоги:

1) функція повинна бути визначена в точці ;

2) функція має границю в точці ;

3) .

Приклад: ; ; ; .

Д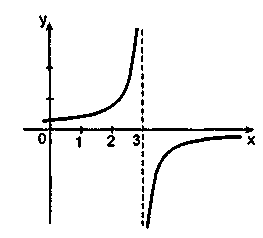 ана функція не буде неперервною в точці , оскільки вона не визначена при . Ті точки, в яких ці умови не виконуються, називаються точками розриву. —точка розриву.

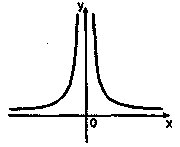
Приклади функцій, які містять точки розриву

—ціла частина

Точки розриву —всі цілочисленні точки

0—точка розриву

Якщо функція неперервна в кожній точці деякого проміжку І, то її називають неперервною на проміжку І.

В шкільному курсі математики:

Графік функції, неперервної на проміжку, — неперервна лінія на цьому проміжку.

Властивості
Ілюстрація	Формулювання	Приклад використання
	1. Якщо неперервна на відрізку функція набуває на кінцях цього відрізка значення різних знаків, то в деякій точці цього відрізка вона набуває значення, яке дорівнює нулю.	— неперервна функція (многочлен); , тому на інтервалі (0;1) існує точка , в якій функція дорівнює 0 (це точка ).
	2. Функція , яка неперервна на відрізку , набуває всіх проміжних значень між значеннями цієї функції у крайніх точках, тобто між та .	— неперервна функція. Якщо , то , . Оскільки , то існує точка , в якій (як відомо, ).
	3. Якщо на інтервалі функція неперервна і не перетворюється на нуль, то на цьому інтервалі функція зберігає сталий знак.	На цій властивості ґрунтується метод інтервалів розв’язування нерівностей виду
Розв’яжемо нерівність , де — довільна функція. Знаходимо область визначення функції . Визначаємо всі нулі функції, тобто розв’язуємо рівняння . Область визначення нулями функції розбиваємо на проміжки. Визначаємо знак функції на кожному проміжку.