7.Аналітична умова рівноваги псзс

Сума збіжних сил ПСЗС перебуває в рівновазі, якщо суми проекцій сил її складаючих на кожну координатну вісь рівні 0.

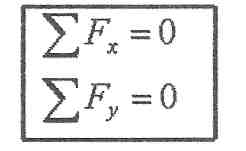
8.Раціональний вибір системи координат

Напрямок осей координат можна вибирати довільно, але для спрощення рішення завдання рекомендується вісь проекцій направляти перпендикулярно лінії дії однієї з невідомих сил. Рівнянь рівноваги два отже, невідомих у завданні повинне бути не більше двох.

Питання для самоперевірки

1. Що зветься плоскою системою збіжних сил.

2. Що таке рівнодіюча для плоскої системи збіжних сил?

3. Які способи складання сил ви знаєте? Охарактеризуйте кожний спосіб та можливість його використання.

4. В якому випадку силовий багатокутник замкнутий?

5. Чи має значення послідовність розташування сил при побудові силового багатокутника?

6. Сформулювати умови рівноваги системи збіжних сил в графічній формі.

7. Сформулюйте теорему про три непаралельні сили, що знаходяться в стані рівноваги.

Питання для самостійного вивчення:

1. Визначення проекції сил на осі

2. Виконання індивідуальних завдань.

Література:

Бычков Д.В. и Миров М.О. Теоретическая механика, 1976. с. 23-32

ЛЕКЦІЯ № 4

Тема 1.2. Плоска система збіжних сил.

План лекції

1. Методика розв’язання задач:

визначення сил реакцій з використанням рівнянь рівноваги ПСЗС.

Порядок розрахунку

Визначення сил реакцій ідеальних зв'язків за допомогою рівнянь рівноваги

1. Викреслити задану схему.

2. Викреслити розрахункову схему (при необхідності вести позначення стержнів (цифрами) і вузлів (буквами))

- визначити точку з'єднання зв'язків, реакції яких необхідно визначити - об'єкт рівноваги (точка А)

- до об'єкта (точці А) додати всі відомі активні сили G, які зійшлися в т.А

- подумки відкинути зв'язку і замінити їх реакціями (S1, S2), (напрямок реакцій залежить від виду зв'язку, найчастіше передбачається, що стрижень розтягнутий і направляємо реакцію від точки)

- Вибрати осі координат (початок координат Т.О поєднуємо з т. А, зручно поставити так, щоб вісь проходила

перпендикулярно лінії дії хоча б однієї з невідомих сил, тобто невідомих повинно бути не більше двох)

- позначити необхідні кути

3. Проектуючи сили і реакції на вибрані осі скласти рівняння рівноваги з умови

Σ F_iх = 0 Σ F_iy = 0

4. З рівнянь визначаємо невідомі необхідні сили реакцій ідеальних зв'язків S1, S2

(Якщо S = 0, то стрижень не працює; S = (-), стрижень стиснутий, реакція спрямована до вузла; S = (+), стрижень розтягнутий, реакція спрямована від вузла)

5. Записати відповідь.

Приклад № 1: Визначити зусилля в нитці й стрижні кронштейна, показаного на рис.1, якщо G=80кH.

Рішення:

1. Розглянемо рівновагу вузла А (точка, у якій сходяться всі стрижні й нитки).

А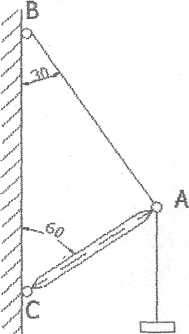

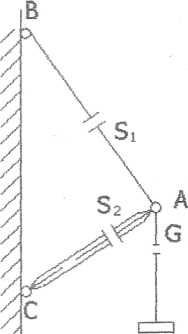
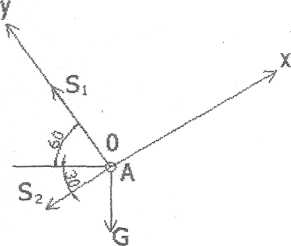
Рис. 1 Рис. 2 Рис. 3

2. Активною силою є вага вантажу G, що спрямована донизу.

3. Відкидаємо зв'язки: стрижень і нитка. Зусилля в нитці позначимо S₁ й направимо від точки А (очевидно, що нитка випробовує розтягання). Зусилля в стрижні позначимо S₂ і направимо теж від точки А (припускаючи що він працює на розтягання). Виконуємо схему дії сил у точці А (розрахункова схема рис.2).

4. Вибираємо положення координатних осей. Початок координат суміщуємо із точкою А. Вісь х суміщуємо з лінією дії зусилля S₁ а вісь у перпендикулярно осі х. Указуємо кути між осями координат і зусиллями S₁ й S₂ (рис.3).

5. Складаємо рівняння рівноваги:

(1) (2)

Із другого рівняння знаходимо:

З першого рівняння знаходимо:

Знак "мінус" перед S₂ указує на те, що стрижень АС не розтягнутий, як передбачалося на початку, а стислий.

Відповідь: S₁=40 кН; S₂=-69,3 кН

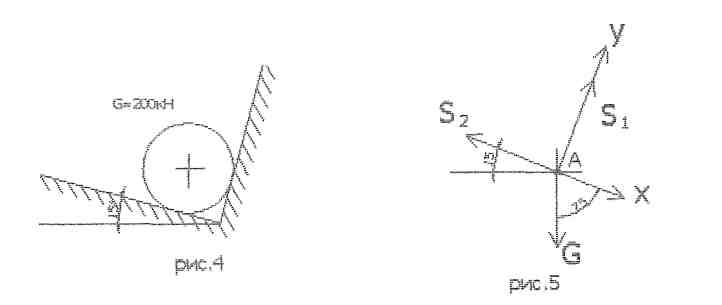
Приклад №2 Визначити невідомі зусилля, показані на рис.4

Рішення:

1. Знаходимо центр збіжних сил. Центром збіжних сил є точка А.

2. Активною силою є вага вантажу G, що спрямована донизу.

3. Зусилля S₁ і S₂ прикладаємо до точки А. (S₁ і S₂ у цьому випадку являються реакціями опору, які направляються по нормалі до відповідної площини).

4. Вибираємо положення координатних осей. (рис.5)

5. Складаємо рівняння рівноваги:

(1)

(2)

Із другого рівняння знаходимо:

Із першого рівняння знаходимо:

Відповідь; S₁=193,2 кН; S₂=51,8 Кн

Питання для самостійного вивчення:

1. Визначення рівнодіючої сили для плоскої системи збіжних сил аналітичним та графічним засобами.

2. Виконання індивідуальних завдань.

Література:

Сетков В.Я. Сборник задач для расчетно-графических работ по технической механике. М.: 1988. с. 4-14

ПРАКТИЧНЕ ЗАНЯТТЯ № 5

Дивись Методичні вказівки до розрахунково-графічних робіт

з дисципліни «Теоретична механіка»

РОЗРАХУНКОВО-ГРАФІЧНА РОБОТА № 1

Тема: Визначення сил реакцій ідеальних зв'язків за допомогою рівнянь рівноваги.

Мета: Закріпити знання з теми «Плоска система збіжних сил».

Навчитися розв’язувати задачі за допомогою рівнянь рівноваги.

Теоретичне обґрунтування:

Збіжними називають дві або більше сили, лінії дії яких перетинаються в одній точці.

Всі питання складання, віднімання та рівноваги збіжних сил можуть бути вирішені аналітичним шляхом – шляхом проектування сил на вісі координат.

З геометрії відомо, що проекцією вектора на вісь зветься добуток величини цього вектора на косинус кута між напрямком вектора та позитивним напрямком осі. Позначивши проекцію сили F на вісь х через F_x ,а на вісь y через F_y получимо:

де α – кут між направленням сили F та віссю х.

Система збіжних сил знаходиться в стані рівноваги, якщо суми проекцій всіх сил,що її складають, на кожну координатну вісь дорівнюють нулю.