§71 Ентропія ідеального газу [8]

1. Обчислимо зміну ентропії ідеального газу. Спочатку розглянемо один моль речовини. Для будь-якого нескінченно малого квазистатичного процесу для ідеального газу згідно з першим законом термодинаміки можемо записати

.

Тут використали, що (індекс « » показує, що величина характеризує один моль речовини) та у відповідності до рівняння Менделєєва-Клапейрона для одного моля газу . Далі згідно до визначення ентропії

.

Теплоємність ідеального газу не залежить від температури. Тоді

. (71.1)

Якщо газ містить молей, то зміну ентропії для цієї кількості газу знайдемо, помноживши (71.1) на (ентропія адитивна величина),

. (71.2)

Потрібно мати на увазі, що цей вираз був отриманий у припущенні, що число молекул у газі залишається сталим.

2. Коли квазистатичний процес є адіабатним, то , а отже, . Таким чином, будь-який квазистатичний адіабатичний процес є процес, що відбувається при сталій ентропії. Тому його можна також назвати ізоентропійним процесом.

Тема 11 Статистичні розподіли §72 Функція розподілу ймовірності. Функції розподілу молекул за швидкостями Максвелла [4,8]

Розглянемо ряд питань з теорії ймовірності. Вони будуть нам потрібними при вивченні елементів статистичної фізики.

1. Нехай деяка величина може набувати ряд дискретних значень:

Якщо провести вимірів величини , то виявиться, що величина набуває значення раз, значення – раз, …, значення – раз і т.д. Зрозуміло, що . Величина

за умови, що (72.1)

називається ймовірністю того, що величина має значення .

Ймовірність має таку властивість

. (72.2)

Тут використали, що . Таким чином, сума ймовірностей всіх можливих значень величини дорівнює одиниці. Про цю властивість говорять як про умову нормування.

2. Знайдемо, використовуючи поняття ймовірності, середнє значення величини . Згідно до визначення середнє значення знаходимо як суму усіх результатів експериментів, що поділена на кількість експериментів

.

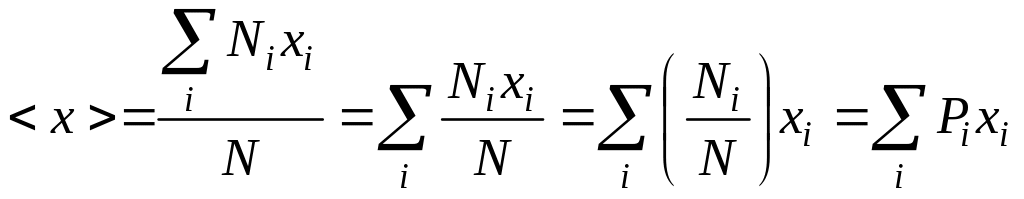Тут взяли до уваги, що величина під час вимірів з’являлася раз. Таким чином, середнє значення величини знаходимо за допомогою співвідношення

. (72.3)

Отримана нами формула дозволяє, знаючи ймовірності різних величин , знайти середнє значення цієї величини.

Розглянемо деяку функцію , аргументом у якої є величина . Будемо вважати, що ймовірність того, що величина набуде значення нам відома. Тоді середнє значення функції , як це отримано в теорії ймовірності, визначається за допомогою співвідношення

. (72.4)

Бачимо, що формули (72.3) та (72.4) подібні.

3. Тепер розглянемо випадок, коли величина може набувати неперервний ряд значень від до (зокрема, і можуть дорівнювати й ). Прикладами таких величин можуть служити модуль поступальної швидкості або кінетична енергія молекули. У цьому випадку число можливих значень нескінченно велике, а кількість молекул хоча й дуже велика, але скінченна. Тому питання про те, яка кількість молекул має точно задане значення величини не має змісту, ця кількість дорівнює нулю.

У розглянутому випадку правомірним є питання про те, яка ймовірність того, що величина має значення, які належать малому інтервалу . Зрозуміло, що при малому ця ймовірність буде пропорційною . Крім того, вона повинна в загальному випадку залежати від того, у якому місці осі розміщений цей інтервал, тобто є функцією . Таким чином,

. (72.5)

Тут індекс біля вказує на значення , біля якого розміщений інтервал шириною . Функція , що входить у формулу (72.5), називається функцією розподілу ймовірності або густиною ймовірності .

Помноживши на повне число молекул , отримаємо кількість молекул , що мають значення , яке знаходяться в межах інтервалу :

. (72.6)

Інтеграл від , узятий по всім можливим значенням (тобто «сума» ), повинен дорівнювати повному числу молекул :

.

Звідси випливає, що

. (72.7)

Формула (72.7) є аналогом формули (72.2) і її також називають умовою нормування.

4. Вираз дає суму значень , яку мають молекул, а «сума» таких виразів, тобто

, (72.8)

дає суму значень всіх молекул. Розділивши цю суму на , отримаємо середнє (за всіма молекулами) значення величини :

. (72.9)

Ця формула є аналогом формули (72.3).

Підставивши у формулу (72.9) замість деяку функцію цієї величини , прийдемо до формули

, (72.10)

яка дозволяє знайти середнє значення довільної функції за відомою густиною ймовірності . За допомогою цієї формули можна обчислити, наприклад, середнє значення :

. (72.11)

5. Розглянемо ідеальний газ, який знаходиться у стані теплової рівноваги. Ми знаємо, що в цьому випадку молекули газу рухаються хаотично. Тобто різні молекули мають різні швидкості як за напрямком, так і за модулем. При цьому з часом через зіткнення ці швидкості змінюються. Поставимо перед собою задачу: описати розподіл молекул за швидкостями.

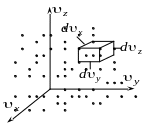
Для того, щоб розв’язати поставлену задачу скористаємося таким прийомом. Уведемо уявний простір швидкостей ( -простір), у якому будемо відкладати уздовж прямокутних координатних осей значення компонент швидкостей окремих молекул (рис. 72.1). Тоді кожній молекулі буде відповідати у просторі швидкостей точка.

Визначимо кількість молекул , компоненти швидкості яких лежать в інтервалі . Зрозуміло, що буде залежати прямо пропорційно від загальної кількості молекул . При малій ця кількість буде пропорційною ширині інтервалу . Крім того, повинна в загальному випадку залежати і від величини швидкості . Узагальнюючи сказане вище, можемо записати

. (72.12)

Рисунок 72.1

Як бачимо, шукану кількість визначає функція . Ця функція називається функцією розподілу молекул за компонентою швидкості . Не важко з’ясувати зміст цієї функції. Перетворимо вираз (72.12), використовуючи, що є ймовірністю того, що швидкість молекули знаходиться в інтервалі

. (72.13)

Порівнюючи формулу (72.13) з (72.5), можемо стверджувати, що є густиною ймовірності розподілу молекул за компонентою швидкості .

Визначимо кількість молекул , модулі швидкості яких лежать в інтервалі . Зрозуміло, що буде залежати прямо пропорційно від загальної кількості молекул . При малій ця кількість буде пропорційною ширині інтервалу . Крім того, повинна в загальному випадку залежати і від величини модуля швидкості . У результаті отримуємо

. (72.14)

Формулу (72.14) визначає функція , яка називається функцією розподілу молекул за абсолютними значеннями швидкостей . Як і в попередньому випадку, неважко показати, що ця функція є густиною ймовірності розподілу молекул за абсолютними значеннями швидкостей молекул .

Визначимо кількість молекул , компоненти швидкостей , , яких лежать в інтервалах , , . Зрозуміло, що буде залежати прямо пропорційно від загальної кількості молекул . При малих ця кількість буде пропорційною об’єму у просторі швидкостей (див. рис. 72.1). Крім того, повинна в загальному випадку залежати і від значень компонент швидкостей , , . Таким чином, отримуємо

. (72.15)

Формулу (72.15) визначає функція , яка називається функцією розподілу молекул за компонентами швидкостей , , . Ця функція є густиною ймовірності розподілу молекул за компонентами швидкостей молекул , , .

Таким чином, задача опису молекул газу у стані теплової рівноваги зводиться до пошуку функцій , , , які називаються функціями розподілу молекул за швидкостями Максвелла.

6. Вигляд функцій , , було встановлено Максвеллом. Для цього він використав рівноправність усіх напрямків руху та незалежність швидкостей , , . У результаті розрахунків було отримано

, (72.16)

, (72.17)

. (72.18)

Формули (72.16)–(72.18) називаються Максвеллівським розподілом молекул ідеального газу за швидкостями. У цих формулах – маса однієї молекули газу; – стала Больцмана; – абсолютна температура.