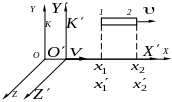- •Конспект лекцій з дисципліни “Фізика”
- •Частина 1
- •Фізика Конспект лекцій
- •6.050801 “Мікро- та наноелектроніка”,
- •6.050802 “Електронні пристрої та системи”,
- •6.050701 “Електротехніка та електротехнології”,
- •6.050201 “Системна інженерія”
- •Частина 1
- •Передмова
- •Розділ 1 Фізичні основи класичної механіки Тема 1 Кінематика §1 Простір і час. Система відліку. Матеріальна точка. Радіус-вектор. Траєкторія, шлях, переміщення [7]
- •§2 Середня й миттєва швидкість. Визначення переміщення і шляху тіла за його швидкістю [4]
- •§3 Прискорення. Визначення швидкості тіла за його прискоренням. Швидкість та координати тіла під час рівноприскореного руху [1]
- •§4 Тангенціальне й нормальне прискорення. Радіус кривизни [1]
- •§5 Вектор кутового зміщення. Кутові швидкість і прискорення. Зв’язок між кутовими й лінійними величинами [1]
- •Тема 2 Динаміка матеріальної точки §6 Перший закон Ньютона. Інерціальні системи відліку [12]
- •§7 Інертність. Маса. Сила. Другий закон Ньютона [7]
- •§8 Третій закон Ньютона. Приклади, що ілюструють третій закон Ньютона [4]
- •§9 Одиниці вимірювань фізичних величин. Основні й похідні одиниці вимірювань. Розмірність [4,13]
- •§10 Закон всесвітнього тяжіння. Сила тяжіння і вага тіла. Вага тіла, що рухається з прискоренням [4]
- •§11 Сила тертя спокою, коефіцієнт тертя спокою. Сила тертя ковзання, коефіцієнт тертя ковзання [4]
- •§12 Сила пружності. Закон Гука. Розтягування і стискування стержнів, модуль Юнга [4]
- •Тема 3 Закони збереження §13 Закон збереження імпульсу для системи матеріальних точок [4]
- •§14 Центр мас системи матеріальних точок. Швидкість і прискорення центра мас [4]
- •§15 Робота змінної сили. Теорема про кінетичну енергію для системи матеріальних точок [7]
- •§16 Робота сили тяжіння, сили всесвітнього тяжіння, сили пружності. Консервативні сили [4,7]
- •§17 Потенціальна енергія. Взаємний зв’язок потенціальної енергії і консервативної сили [4,7]
- •§18 Повна механічна енергія системи матеріальних точок. Закон збереження повної механічної енергії для системи матеріальних точок. Робота неконсервативних сил [4]
- •§19 Зіткнення тіл. Швидкості тіл після центрального абсолютно пружного та абсолютно непружного ударів [4]
- •Тема 4 Тверде тіло в механіці §20 Момент сили і момент імпульсу. Рівняння моментів для матеріальної точки [7]
- •§21 Рівняння моментів для системи матеріальних точок. Закон збереження моменту імпульсу [1]
- •§22 Швидкість довільної точки твердого тіла під час його плоского руху. Кутова швидкість обертання твердого тіла. Миттєва вісь обертання [4]
- •§23 Рух центра мас твердого тіла. Прискорення центра мас твердого тіла [4]
- •§24 Обертання твердого тіла навколо нерухомої осі. Рівняння динаміки обертального руху відносно нерухомої осі [4]
- •§25 Момент інерції циліндра (диска) відносно осі симетрії [4]
- •§26 Момент інерції стержня [4]
- •§27 Теорема Гюйгенса-Штейнера [7]
- •§28 Робота тіла, що обертається навколо нерухомої осі [4]
- •§29 Кінетична енергія твердого тіла за умови плоского руху [4]
- •§30 Рівняння руху і рівноваги твердого тіла. Прискорення циліндра, який котиться без ковзання з похилої площини [1,7]
- •Тема 5 Неінерційні системи відліку §31 Неінерціальні системи відліку. Сили інерції. Поступальна сила інерції [7]
- •§32 Відцентрова сила інерції [4]
- •§33 Сила Коріоліса [4]
- •Тема 6 Механіка рідин §34 Методи Лагранжа та Ейлера для опису течії рідини. Трубка течії [4,14]
- •§35 Теорема про нерозривність потоку [4]
- •§36 Рівняння Бернуллі [4]
- •§37 Витікання рідини з малого отвору. Формула Торрічеллі [4]
- •§38 Сила внутрішнього тертя. Формула Ньютона для сили внутрішнього тертя. В’язкість. Ламінарна і турбулентна течія рідини. Число Рейнольдса [1]
- •§39 Рух тіл у рідинах та газах. Сила лобового опору. Піднімальна сила. Парадокс д’Аламбера. Вплив в’язкості на характер обтікання тіла рідиною. Сила Стокса [4]
- •Тема 7 Елементи спеціальної теорії відносності §40 Принцип відносності Галілея. Перетворення Галілея [4]
- •§41 Постулати спеціальної теорії відносності. Відносність одночасності [4,7]
- •§42 Перетворення Лоренца [4]
- •§43 Перетворення швидкостей у спеціальній теорії відносності [4]
- •§44 Лоренцеве скорочення довжини [4]
- •§45 Релятивістське уповільнення ходу часу [4]
- •§46 Інтервал і його інваріантність. Швидкість світла як гранична швидкість поширення довільного сигналу [4]
- •§47 Закон збереження імпульсу в спеціальній теорії відносності. Релятивістське рівняння динаміки [4]
- •§48 Кінетична енергія в спеціальній теорії відносності [4]
- •§49 Енергія спокою. Повна енергія. Взаємозв'язок маси й енергії спокою [4]
- •Розділ 2 Основи молекулярної фізики і термодинаміки Тема 8 Макроскопічний стан §50 Статистичний і термодинамічний підходи до вивчення теплових властивостей макроскопічних тіл [4]
- •§51 Термодинамічна система. Параметри стану системи. Рівноважні та нерівноважні стани. Термодинамічний процес. Квазистатичний процес [4]
- •§52 Температура. Термометр. Загальний (нульовий) закон термодинаміки. Основна властивість температури. Шкала температур Цельсія. Абсолютна температура [8]
- •§53 Основні положення молекулярно-кінетичної теорії речовини. Броунівський рух [4,15]
- •§54 Рівняння стану термодинамічної системи. Рівняння стану ідеального газу як результат узагальнення експериментальних досліджень [4]
- •§55 Барометрична формула [4]
- •§56 Тиск ідеального газу з точки зору молекулярно-кінетичної теорії [8]
- •§57 Молекулярно-кінетичний зміст абсолютної температури [4]
- •§58 Ступені вільності механічної системи. Теорема про рівномірний розподіл кінетичної енергії за ступенями вільності. Середня енергія молекули [4]
- •Тема 9 Перший закон термодинаміки §59 Внутрішня енергія термодинамічної системи [4]
- •§60 Робота, що виконується тілом при змінах його об'єму [4,8]
- •§61 Кількість теплоти. Перший закон термодинаміки. Вічний двигун першого роду [8]
- •§62 Теплоємність. Питома й молярна теплоємність. Теплоємність при постійному тиску, при постійному об'ємі. Внутрішня енергія ідеального газу. Рівняння Майєра. Стала адіабати [4]
- •§63 Рівняння адіабати ідеального газу [4]
- •§64 Політропічні процеси. Показник політропи. Рівняння політропи [4]
- •§65 Робота, що виконується газом при ізопроцесах [4]
- •§66 Класична теорія теплоємності ідеального газу [4]
- •Тема 10 Другий закон термодинаміки §67 Будова і принцип дії теплової машини. Коефіцієнт корисної дії теплової машини [8]
- •§68 Вічний двигун другого роду. Другий закон термодинаміки. Формулювання другого закону термодинаміки Томсона і Клаузіуса [8]
- •§69 Оборотні і необоротні процеси. Цикл Карно. Перша і друга теореми Карно [8]
- •§70 Нерівність і рівність Клаузіуса. Ентропія. Закон зростання ентропії [8]
- •§71 Ентропія ідеального газу [8]
- •Тема 11 Статистичні розподіли §72 Функція розподілу ймовірності. Функції розподілу молекул за швидкостями Максвелла [4,8]
- •§73 Середні швидкості молекул. Число ударів молекул об одиничну поверхню за одиницю часу [8]
- •§74 Розподіл Больцмана [4]
- •Тема 12 Явища перенесення §75 Довжина вільного пробігу молекул [8]
- •§76 Емпіричні рівняння, що описують дифузію, теплопровідність, внутрішнє тертя. Якісне пояснення явищ перенесення в газах [4]
- •Тема 13 Реальні гази та рідкий стан §77 Реальні гази. Рівняння Ван-дер-Ваальса [4,8]
- •§78 Ізотерми Ван-дер-Ваальсівського газу. Критичні температура, тиск, об'єм і їх зв'язок із сталими Ван-дер-Ваальса [4]
- •§79 Експериментальні ізотерми [4]
- •§80 Фаза в термодинаміці. Фазове перетворення першого і другого роду. Приклади фазових перетворень. Діаграма станів [4]
- •§81 Будова рідин. Поверхневий натяг рідин. Коефіцієнт поверхневого натягу. Крайовий кут [4]
- •§82 Формула Лапласа. Капілярні явища. Висота піднімання й опускання рідини в капілярах [4]
- •Розділ 3 Електрика Тема 14 Електричне поле у вакуумі §83 Явище електризації. Електричний заряд. Елементарний електричний заряд. Дискретність заряду. Закон збереження електричного заряду [5,16]
- •§84 Закон Кулона. Принцип суперпозиції електричних сил. Одиниці вимірювання заряду [5]
- •§85 Електричне поле. Напруженість електричного поля. Напруженість електричного поля точкового заряду. Принцип суперпозиції електричних полів [5]
- •§87 Зв’язок між напруженістю електростатичного поля і потенціалом. Силові лінії та еквіпотенціальні поверхні. Перпендикулярність силових ліній і еквіпотенціальних поверхонь [5]
- •§88 Поле електричного диполя [5]
- •§89 Потік вектора. Теорема Гаусса для вектора напруженості електричного поля [9]
- •§90 Напруженість електричного поля нескінченної однорідно зарядженої пластини [2]
- •§91 Напруженість електричного поля однорідно зарядженої циліндричної поверхні [2]
- •§92 Напруженість електричного поля об’ємно зарядженої кулі [2]
- •§93 Диференціальна форма електростатичної теореми Гаусса. Значення теореми Гаусса в теорії електрики [9]
- •Тема 15 Електричне поле у діелектриках §94 Поляризація діелектриків. Зв’язані заряди. Механізми поляризації [9]
- •§95 Вектор поляризації. Поверхнева густина зв’язаних зарядів. Зв’язаний заряд усередині діелектрика [9]
- •§96 Вектор електричної індукції. Теорема Гаусса для діелектриків [9]
- •§97 Поляризованість і діелектрична проникність [9]
- •§98 Умови на межі поділу двох діелектриків [17]
- •Тема 16 Провідники в електричному полі §100 Умови рівноваги зарядів на провіднику. Електричне поле усередині провідника. Напруженість електричного поля біля поверхні провідника [9]
- •§101 Електроємність відокремленого провідника. Ємність кулі [5]
- •§102 Конденсатор. Ємність конденсатора. Ємність плоского і циліндричного конденсатора. Ємність системи, що складається з послідовно та паралельно з’єднаних конденсаторів [5]
- •Тема 17 Енергія електричного поля §103 Енергія системи точкових зарядів [5]
- •§104 Енергія зарядженого провідника. Енергія зарядженого конденсатора [5]
- •§105 Енергія електричного поля [5]
- •Тема 18 Постійний електричний струм §106 Електричний струм. Густина електричного струму з мікроскопічної точки зору. Рівняння неперервності для електричного заряду [5,9]
- •§107 Сторонні сили. Електрорушійна сила. Робота над електричним зарядом на ділянці кола [5]
- •§108 Закон Ома для однорідної ділянки кола. Залежність опору від геометричних розмірів провідника. Закон Ома в диференціальній формі. Провідність [5]
- •§109 Закон Ома для неоднорідної ділянки кола в диференціальній і інтегральній формі. Закон Ома для замкненого кола [5]
- •§110 Правила Кірхгофа [5]
- •§111 Потужність струму. Закон Джоуля-Ленца в інтегральній і диференціальній формі [5]
- •§112 Процеси встановлення струму під час заряду і розряду конденсатора [9]
- •§113 Природа носіїв струму в металах. Дослід Рікке. Ідея Лоренца визначення відношення заряду до маси носія електричного струму в металах. Дослід Толмена і Стюарта [2]
- •§115 Електричний струм у газах. Процеси, що приводять до виникнення носіїв струму при самостійному газовому розряді. Самостійний та несамостійний розряди [5]
- •Список літератури
- •Предметний покажчик
- •Фізика Конспект лекцій
- •Частина 1
§44 Лоренцеве скорочення довжини [4]
|
Рисунок 44.1 |
Для визначення довжини
стержня в системі
,
де стержень знаходиться у стані спокою,
потрібно прикласти до нього масштабну
лінійку й визначити координату
![]() одного кінця стержня, а потім координату
одного кінця стержня, а потім координату
![]() іншого кінця. Різниця координат дасть
довжину стержня
в системі
:
іншого кінця. Різниця координат дасть
довжину стержня
в системі
:
![]() .
.
Довжину , що виміряна в системі відліку, в якій тіло знаходиться у стані спокою, називають власною довжиною.
У системі
виміряти довжину стержня складніше.
Відносно системи
стержень рухається зі швидкістю
,
яка дорівнює швидкості
,
з якою система рухається
![]() відносно системи
.
Оскільки стержень рухається, потрібно
визначити координати його кінців
відносно системи
.
Оскільки стержень рухається, потрібно
визначити координати його кінців
![]() і
і
![]() в один і той же момент часу
в один і той же момент часу
![]() .
Тут
момент часу, коли проводимо вимірювання
координати
.
Тут
момент часу, коли проводимо вимірювання
координати
![]() ,
,
![]() момент часу, коли проводимо вимірювання
координати
момент часу, коли проводимо вимірювання
координати
![]() .
Різниця координат дасть довжину стержня
в системі
:
.
Різниця координат дасть довжину стержня
в системі
:
![]() .
.
Щоб порівняти довжини і використаємо формули перетворення Лоренца
![]() .
.
Звідси
![]() .
.
Замінивши різниці координат довжинами стержня, а швидкість системи відносно , що дорівнює швидкості стержня , з якої він рухається в системі , прийдемо до формули
![]() . (44.1)
. (44.1)
Таким чином, довжина стержня, що рухається, виявляється менше тієї, яку він має у стані спокою. Аналогічний ефект спостерігається для тіл будь-якої форми: у напрямку руху лінійні розміри тіла скорочуються тим більше, чим більше швидкість руху. Це явище називається скороченням довжини Лоренца. Поперечні розміри тіла не змінюються. У результаті цього, наприклад, куля набуває форму еліпсоїда, сплющеного у напрямку руху.
§45 Релятивістське уповільнення ходу часу [4]
1. Порівняємо проміжки часу в інерціальних системах відліку й . Вважаємо, що система рухається відносно системи зі швидкістю .
Нехай у системі
в одній і тій же точці з координатою
![]() відбуваються в моменти часу
відбуваються в моменти часу
![]() й
й
![]() дві якихось події (
дві якихось події (![]() – координата події 1,
– координата події 1,
![]() – координата події 2). Це можуть бути,
наприклад, народження елементарної
частки (подія 1) і її наступний розпад
(подія 2). У системі
ці події розділені проміжком часу
– координата події 2). Це можуть бути,
наприклад, народження елементарної
частки (подія 1) і її наступний розпад
(подія 2). У системі
ці події розділені проміжком часу
![]() .
.
Знайдемо проміжок часу між цими подіями в системі , відносно якої система рухається зі швидкістю . Для цього визначимо в системі моменти часу й , що відповідають моментам і , і утворимо їхню різницю:
![]() .
.
Для зіставлення часу в системі й використаємо перетворення Лоренца
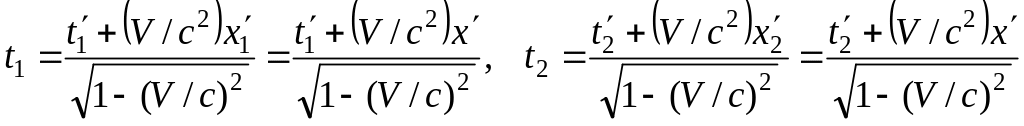 .
.
Звідси знаходимо
![]() . (45.2)
. (45.2)
У системі
події відбуваються в одній і тій же
точці. Це означає, що
є проміжком часу, який вимірюється
нерухомим у цій системі відліку
годинником. Такий час називається
власним часом і позначається
![]() .
Власним часом називають
проміжок часу між двома подіями, який
вимірюється в системі відліку, де ці
події відбуваються в одній і тій же
точці. Таким чином,
.
Власним часом називають
проміжок часу між двома подіями, який
вимірюється в системі відліку, де ці
події відбуваються в одній і тій же
точці. Таким чином,
![]() .
.
Величина
являє собою проміжок часу між тими ж
подіями, які вимірюються годинниками
системи
,
відносно якої точка, в якій відбуваються
ці події рухається зі швидкістю
![]() .
З урахуванням вищесказаного формулу
(45.2) можна подати у вигляді
.
З урахуванням вищесказаного формулу
(45.2) можна подати у вигляді
![]() . (45.3)
. (45.3)
З отриманої формули випливає, що власний час менше часу, відліченого за годинниками, які рухаються відносно точки, де ці події відбуваються.
З погляду спостерігача,
який знаходиться у системі
![]() є проміжок часу між подіями, який
вимірюється нерухомими годинниками, а
– проміжок часу, який вимірюється
годинником, що рухається зі швидкістю
.
Оскільки
є проміжок часу між подіями, який
вимірюється нерухомими годинниками, а
– проміжок часу, який вимірюється
годинником, що рухається зі швидкістю
.
Оскільки
![]() (див.(45.3)), то можна сказати, що годинники,
які рухаються, ідуть повільніше, ніж
нерухомі годинники.
(див.(45.3)), то можна сказати, що годинники,
які рухаються, ідуть повільніше, ніж
нерухомі годинники.