2 Векторный метод конечных элементов

Метод конечных элементов (МКЭ) оказался мощным и гибким инструментом для численного решения широкого класса физических задач, включая задачи электростатики, магнитостатики, токовихревые задачи и общие задачи электромагнетизма, а его векторный аналог оказался подходящим подходом для аппроксимации физических характеристик электромагнитного поля.

2.1 История развития векторного метода конечных элементов

Считается, что начало векторному МКЭ положили работы Ж. К. Неделека. В 1980, 1986 годах им была предложена теория edge- и face- векторных элементов высоких порядков [19, 20]. Он ввел новые семейства векторных неконформных конечных элементов – конечные элементы на кубах и тетраэдрах. Эти семейства являются конформными в специальных пространствах H(rot, Ω) и H(div, Ω). Пространствa H(rot, Ω) и H(div, Ω) играют особую роль при численном решении уравнений Максвелла, так как решения принадлежит этим же пространствам: и . Таким образом выделяются два семейства векторных конечных элементов: дивергентно-конформные и роторно-конформные элементы, обеспечивающие непрерывность на межэлементных границах в смысле дивергентного оператора (т.е. нормальная непрерывность) и роторного оператора (т.е. тангенциальная непрерывность), соответственно. Таким образом, дивергентно-конформные элементы подходят для дискретизации электрической и магнитной индукции, и , в то время как роторно-конформные элементы подходят для аппроксимации электрического и магнитного полей, и .

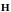В середине 1980-х было доказано, что стандартный подход аппроксимации каждой компоненты векторного поля как отдельной скалярной функции неэффективен [4]. Трудности, возникающие при обработке межфрагментарных и граничных условий, при моделировании сингулярностей электромагнитного поля на острых углах и ребрах, появление ложных (не имеющих физической интерпретации) мод – снижают производительность метода и негативно влияют на точность вычислений. Векторный метод конечных элементов (ВМКЭ) высоко эффективен при решении задач электромагнетизма, лишён перечисленных недостатков узлового МКЭ. В векторном МКЭ используется базис, обеспечивающий непрерывность тангенциальной компоненты напряженности электрического поля (напряженности магнитного поля ) на межфрагментарных границах, при этом нормальная компонента векторного поля ( ) может быть разрывной. Такое ослабление непрерывности позволяет подавить ложные моды и значительно облегчает задание корректных с физической точки зрения краевых и граничных условий. Кроме того, оно существенно повышает точность моделирования поля около сингулярностей. В настоящее время для решения задач электромагнетизма широко используется именно векторный метод конечных элементов.

При решении задач моделирования электромагнитных полей в частотной области в широком диапазоне частот (от 100 кГц до 10ГГц) в областях с разрывными электрофизическими характеристиками одной из наиболее важных и сложнорешаемых проблем является обоснованный выбор типа базисных функций. Поэтому в последние годы среди исследователей возрос интерес именно к этой проблеме.

В работах Неделека [19, 20] был дан общий подход к формированию векторных конечных элементов, в то время как специальный векторный базис введен не был. В дальнейшем этим вопросом занимались многие исследователи, предлагавшие свои варианты решения проблемы построения векторного базиса [4, 21-28].

Существуют различные подходы к вопросу построения векторных базисных функций: исходя из геометрических свойств базисных функций [4, 21], на основе ортогональных полиномов[25-27], численного интегрирования линейных функционалов [22, 24].

В [25] базисные функции строятся на основе полиномов Лежандра.

В [27] базис конструируется на основе полиномов Лобатто:

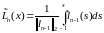
где n – порядок полинома, 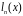– полином Лежандра.

В [28] приводятся основные выражения для построения векторного базиса в пространстве на основе полиномов Якоби:

Следует отметить также, что классы задач моделирования трехмерного электромагнитного поля определяют тип ассоциированных с особенностями рассматриваемого класса задач векторных базисных функций. Этот вопрос тоже рассматривается некоторыми исследователями, но пока что в значительно меньшей степени [29].