10. Показательное распределение
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью
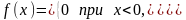
где
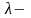постоянная
положительная величина, параметр
показательного распределения.
Функция распределения показательного закона
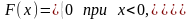
Графики плотности распределения и функции распределения случайной величины Х, нормально распределённой на отрезке , изображены на рис.6 и 7:
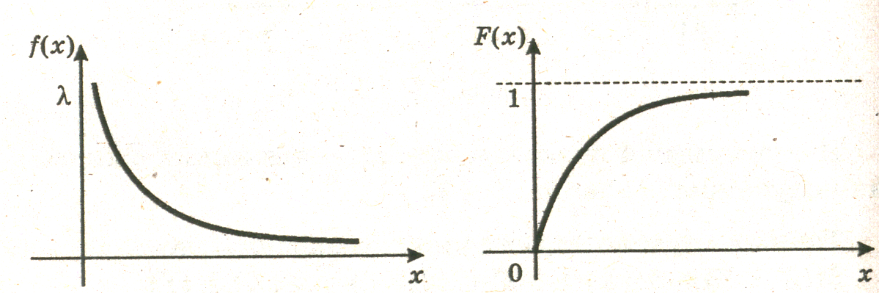
Рис. 6 Рис.7
Вероятность попадания в интервал (а,b) непрерывной случайной величины Х, распределённой по показательному закону,
.
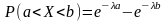Математическое ожидание, дисперсия и среднее квадратическое отклонение показательного распределения соответственно равны:
.
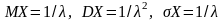Характеристическое свойство. Математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой, т. е.
.
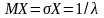Пример.
Непрерывная
случайная величина Х
распределена по показательному закону,
заданному плотностью вероятностью
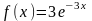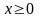при
;
при
.
Найти вероятность того, что в результате
испытания Х
попадает в интервал (0,13; 0,7). Найти
дисперсию.
Решение. Используем формулу .
Учитывая,
что, по условию,
,
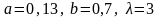и пользуясь таблицей значений функции
,
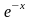получим
.
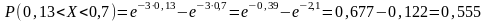Найдём
дисперсию по формуле
.
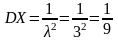Тема. Выборочный метод
1. Вариационные ряды. Таблица частот
Предположим, на нескольких предприятиях изготавливают однотипные объекты, которые обладают некоторым признаком.
Чтобы определить качество производимой продукции по данному признаку, необходимо исследовать большой объём объектов – N, так называемой совокупности.
Положим, что имеется N объектов, каждому из которых присуще определённое значение числовой характеристики. Такая совокупность N объектов называется генеральной совокупностью, т.е. совокупностью всех возможных значений случайной величины Х.
Совокупность
n
возможных значений х:
,
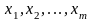(1)
полученных в результате n независимых опытов (наблюдений), называется выборкой, или статистическим рядом объёма n.
Различные значения случайной величины, содержащие в выборке (1), называются вариантами. Система вариант , расположенных в порядке возрастания, называется вариационным рядом.
Любую
числовую функцию
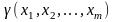от результатов наблюдений
исследуемой случайной величины называют
статистикой.
Частотой
,
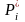называется отношение количества
повторений i-той
варианты (
)
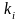к объёму всей совокупности (n):
.
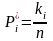Сумма всех должна быть равна 1, а сумма – равна n.
Вариационные (статистические) ряды бывают дискретными и интервальными.
Когда рассматривают дискретную случайную величину, то её вариационный ряд можно изобразить в виде таблицы, в первой строке которой расположены варианты, а во второй – соответствующие им частоты:
-
…
…
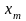
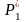
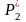
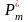
Эту таблицу называют таблицей частот, или эмпирическим законом распределения дискретной случайной величины.