Образовательный маршрут по дисциплине «Теория вероятностей и математическая статистика»

1 контрольная работа, дифференцированный зачёт

Перечень тем с/р и литература

Решение комбинаторных задач на применение формул размещения, перестановки, сочетания. Составление примеров на различные виды событий	10/10
Решение ситуационных задач. Нахождение вероятностей событий с помощью формул полной вероятности, Байеса, Бернулли, Муавра-Лапласа, Пуассона и классического определения.	20/30
Решение ситуационных задач на вычисление числовых характеристик случайной величины двумя способами. Составление функции распределения и плотности вероятности. Исследование многомерных ДСВ и НСВ. Предельные теоремы теории вероятностей	20/50
Построение таблицы частот, полигона и гистограммы. Нахождение числовых характеристик. Распределение случайных величин в пакете MS Excel. Точечные оценки параметров распределения. Интервальные оценки параметров распределения. Построение доверительных интервалов. Проверка статистических гипотез	20/70
Графы, орграфы, деревья. Путь в графе. Длина пути. Ребро. Цикл. Виды графов. Операции над графами. Способы задания графа. Применение графов. Решение задач на построение графов	17/87

1. Андронов А.М. Теория вероятностей и математическая статистика / Е.А. Копытов, Л.Я. Гринглаз. – СПб.: Питер, 2008. – 461 с.

2. Баврин И.И. Теория вероятностей математическая статистика. – М.: Высшая школа, 2007. – 161 с.

3. Бочаров П. П., Печинкин А. В. Теория вероятностей. Математическая статистика. 2007. – 296 с.Боровиков В.П. STATISTICA: искусство анализа данных на компьютере. Для профессионалов. – СПб.: Питер, 2008. – 384 с.

Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2010. – 479 с.

4. Гончаров Г.А. Элементы дискретной математики. – М.: ФОРУМ: ИНФРА-М, 2009. – 128 с.Дьяконов В. Mathcad 2001: учебный курс. – СПб.: Питер, 2006. – 624 с.

5. Максимова О.В. Теория вероятностей и математическая статистика. – Ростов н/Д.: Феникс, 2008. – 347 с.

6. Миронова Н.П. Теория вероятностей и математическая статистика. – Ростов н/Д.: Феникс, 2008. – 212 с.

7. Спирин П.А. Теория вероятностей и математическая статистика / М.С. Спирина. – М.: Академия, 2007. – 352 с.

8. Спирин П.А. Дискретная математика/ М.С. Спирина. – М.: Академия, 2007. – 368 с.

9. Боровиков С.Н. Прогнозирование в системе Statistica в среде Windows. Основы теории и интенсивная практика на компьютере/ Г. И. Ивченко. – М.: Финансы и статистика, 2008. – 384 с.

Теоретический материал для самостоятельного изучения по темам

Тема. Комбинаторика. Правила сложения и умножения

Комбинаторика – раздел математики, посвящённый решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами.

Комбинаторика занимается изучением способов выбора и подсчета комбинаций. В комбинаторике существуют два правила: правило сложения и правило умножения.

Рассмотрим два конечных множества А и В. Обозначим через n(A) –число элементов множества А (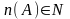 ), n(B) – число элементов множества В (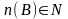 ). Отметим, число элементов пустого множества равно нулю, т.е. .

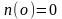Правило сложения. Если объект 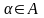можно выбрать 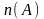числом способов, объект 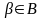можно выбрать 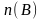числом способов, то выбор хотя бы одного из объектов 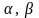можно осуществить 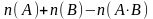числом способов, т.е.

.

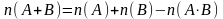Замечание. Для трёх конечных множеств А, В, С имеем

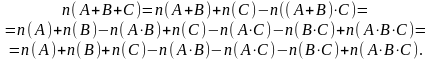
Пример. Сколько чисел среди первых ста натуральных чисел, не делящихся ни на 2, ни на 3, ни на 5.

Решение. Пусть А – множество чисел, делящихся на 2, В – множество чисел, делящихся на 3, С– множество чисел, делящихся на 5, D – множество чисел, не делящихся ни на 2, ни на 3, ни на 5, 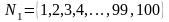. Множество 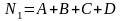. Нужно найти 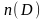. Пересечение двух множеств А+В+С и D есть пустое множество, т.е. 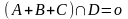. Тогда

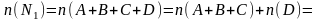
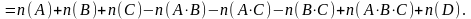
Отсюда

. (1)

Здесь

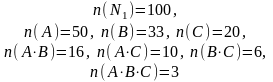
(вычислили с помощью арифметической прогрессии).

Подставляя соответствующие значения в формулу (1), получим

.

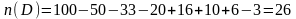Правило умножения. Если объект можно выбрать числом способов, объект можно выбрать числом способов, то одновременный выбор объектов можно осуществить 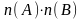числом способов, при условии, что независимые объекты.

Пример. 4 мальчика и 4 девочки садятся на 8 подряд расположенных стульев: мальчики – с четными номерами, а девочки – с нечётными. Сколькими способами это можно сделать?

Решение. Пусть А – множество мальчиков, а В – множество девочек. Первый мальчик может выбрать одно из четырёх мест, т.е. может занять место четырьмя способами. Второй может занять место тремя способами, третий – двумя, четвертый – одним. Тогда по правилу умножения: 4·3·2·1=24. Т.е. четыре мальчика могут занять четыре места двадцатью четырьмя способами. Столько же возможностей у девочек. Тогда по правилу умножения число способов занять места указанным способом равна 576=24·24.

Замечание. Правило умножения можно обобщить на большое число множеств:

,

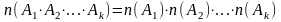при условии, что способы выбора объектов каждого множества независимы.

Тема. Выборки, соединения и комбинации

1.Размещения, перестановки и сочетания без повторений

Пусть A - конечное множество, n(A) – объём множества.

Выборки будем составлять из элементов множества А, которые как объекты не повторяются.

Порядком во множестве из n элементов называется всякое взаимно однозначное отображение этого множества на подмножество N {1,2,3,..,n}.

Количество порядков элементов множества А равно n! (n факториал). Выборки могут быть упорядоченные и неупорядоченные. Выборки делятся на размещение, перестановки и сочетание.

Определение 1. Размещениями без повторений из n элементов множества А по k элементов этого множества называются упорядоченные выборки без повторений, составленные из элементов множества А, имеющие один и тот же объём k.

В размещениях без повторений важен порядок расположения элементов, можно изменить состав соединения, что приведёт к новой выборке, элементы которой не повторяются.

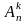- размещение из n по k без повторений: .

Определение 2. Перестановками без повторений из k элементов множества А по k элементов этого множества называются упорядоченные выборки без повторений, составленные из элементов множества А, имеющие один и тот же объём k.

В перестановках без повторений важен порядок расположения элементов, состав выборок изменить нельзя, элементы в соединениях не повторяются.

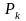- перестановки k по k без повторений: .

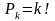Определение 3. Сочетаниями без повторений из n элементов множества А по k элементов этого множества называются неупорядоченные выборки без повторений, составленные из элементов множества А, имеющие один и тот же объём k.

В сочетаниях без повторений не важен порядок расположения элементов, состав соединения изменить можно, элементы в выборке не повторяются.

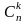- сочетания из n по k без повторений: .

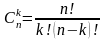Алгоритм решения задач:

1. записать множество из элементов, из которых будет производиться выборка;

2. записать объём множества;

3. записать объём выборки;

4. составить несколько выборок из элементов множества, по которым дать характеристику всех возможных выборок этого множества;

5. по характеристике выбрать нужную формулу.

Пример 1. В группе 5 уроков. Всего дисциплин 7. Сколькими способами можно составить расписание уроков, если в день проводятся уроки различных дисциплин?

Решение.

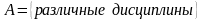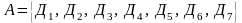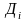1. Множество , , где - одно из наименований дисциплин и .

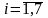2. Объём множества: .

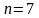3. Объём выборки: .

4. Составим несколько выборок:

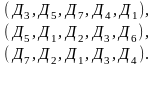
Видим, что состав изменить можно, изменение порядка приведёт к новому соединению, т.е. порядок расположения элементов важен, элементы не повторяются. Следовательно, число всех соединений совпадает с числом размещений без повторений.

5. .

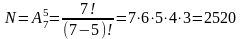Пример 2. Сколькими способами можно избрать из 15 человек делегацию из 5 лиц.

Решение.

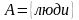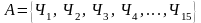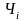1. Множество , , где - одно из наименований дисциплин и .

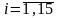2. Объём множества: .

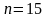3. Объём выборки: .

4. Составим несколько выборок:

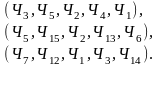
Видим, что состав изменить можно, изменение порядка не приведёт к новому соединению, т.е. порядок расположения элементов не важен, элементы не повторяются. Следовательно, число всех соединений совпадает с числом сочетаний без повторений.

5. .

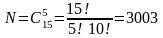Пример 3. На полке 8 книг. Сколькими способами можно расставить 8 книг так, чтобы 2 определённые книги стояли рядом?

Решение.

В задаче 2 выбора: 1) расставляют 7 книг (две определённые книги принимаем за одну);

2) расставляют 2 определённые книги.

Рассмотрим первый выбор.

1. Множество .

2. Объём множества: .

3. Объём выборки: .

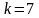4. Составим несколько выборок:

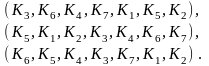
Здесь состав изменить нельзя, изменение порядка приведёт к новому соединению, т.е. порядок расположения элементов важен, элементы не повторяться. Следовательно, число всех соединений совпадает с числом перестановок без повторений.

5. .

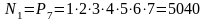Рассмотрим второй выбор.

1. Множество .

2. Объём множества: .

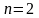3. Объём выборки: .

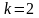4. Составим выборки:

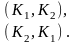
Видим, что состав изменить нельзя, изменение порядка приведёт к новому соединению, т.е. порядок расположения элементов важен, элементы не повторяются. Следовательно, число всех соединений совпадает с числом перестановок без повторений.

5. .

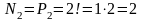Так как два выбора происходят одновременно, то по правилу умножения следует, что число способов расставить книги есть произведение перестановок:

.
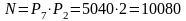