Задания для лабораторной работы
1) Решить задачу выбора объема производства с теми же условими, но для линейной функции спроса.
2) Построить графики средних издержек и среднего дохода.
Решить задачу для случая растущих предельных издержек: VC=55 + Q.
Лабораторная работа №4 – Решение задач межотраслевого баланса в среде MathCad Пример решения
Воспользуемся возможностями системы MathCAD для решения задачи наблюдаемости модели межотраслевого баланса Леонтьева. По заданному вектору валового продукта X найдем вектор конечного продукта Y. Рассчитаем также межотраслевые поставки. Условия:
Введем единичную матрицу E. Далее просто воспользуемся формулой для задачи наблюдаемости Y=(E-A) · X. Выведем полученный вектор Y на экран. Решение показано на рисунке 4.1а.
Для расчета матрицы межотраслевых поставок установим служебную переменную ORIGIN:=1. Далее создадим две интервальные переменные для индексов по строкам и столбцам. После этого вводим формулу для элемента матрицы W. Решение показано на рисунке 4.1б.
а) |
б) |
Рисунок 4.1 – Решение задачи наблюдаемости и расчет межотраслевых поставок
Задания для лабораторной работы
1) Решить задачу синтеза:
найти матрицу коэффициентов полных затрат;
найти вектор выпуска Х;
найти матрицу коэффициентов косвенных затрат;
вывести матрицу межотраслевых поставок;
рассчитать вектор затрат труда;
найти вектор полных затрат труда.
Исходные данные:
Лабораторная работа №5 – Расчет параметров производственной функции Кобба-Дугласа Постановка задачи
Имеются данные о затратах труда L, капитала K и об объеме выпуска Y за несколько лет. Необходимо с помощью регрессионного анализа рассчитать коэффициенты производной функции в форме Кобба-Дугласа:
Для решения задачи использовать данные из таблицы. Следует оценить коэффициент детерминации регрессионного уравнения и убедиться в значимости коэффициентов уравнения. С помощью производственной функции найти значение выпуска, соответствующее значениям K=200, L=100. Оценить предельную норму замещения труда капиталом в этой точке. Расчет производить с помощью MS Excel. Построить трехмерный график функции и ее изокванты в пакете MathCAD.
Исходных данные:
-
L
K
Y
100
200
1680
220
300
2775
150
240
2130
130
190
1730
180
400
3275
140
240
2100
150
310
2580
140
200
1830
200
380
3230
180
350
2970
Пример решения
Введем данные таблицы в MS Excel. Для построения регрессионного уравнения необходимо провести линеаризацию уравнения. Возьмем натуральный логарифм обеих его частей и преобразуем:
ln Y = ln a + 1 ln L + 2 ln K
Мы получили линейное уравнение, куда входят ln Y, ln L и ln K. Коэффициенты уравнения ln(a), 1, 2. Мы должны строить регрессионное уравнение по переменным ln(Y), ln(L) и ln(K), для чего воспользуемся функцией ln() системы Excel. Соответствующие столбцы (D,E,F) показаны на рисунке 5.1.
Рисунок 5.1 – Исходные данные для расчетов
Теперь построим линейное регрессионное уравнение с помощью пункта меню «Сервис - > Анализ данных». Возможно, надстройка не установлена, в этом случае нужно добавить ее (она называется «Пакет анализа») с помощью пункта меню «Сервис - > Надстройки».
В появившемся списке выбираем инструмент «Регрессия». Диалог для построения уравнения показан на рисунке 5.2. Здесь мы должны указать интервал зависимой переменной (Входной интервал Y), в качестве этого интервала мы выбираем F1:F11, как это показано на рисунке. В нашем примере роль зависимой переменной играет ln(Y). Далее указываем интервал независимых переменных (Входной интервал X), в нашем случае это интервал D1:D11, который соответствует столбцам со значениями логарифмов затрат труда и капитала. Установим флажок «Метки», так как в интервалы мы включили и названия столбцов.
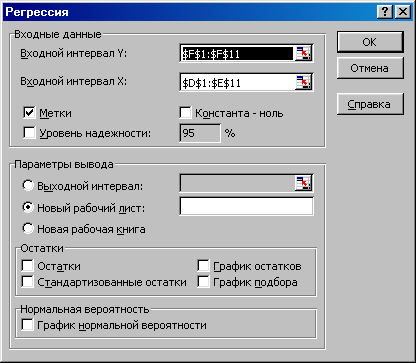
Рисунок 5.2 – Построение регрессионного уравнения
Полученный результат будет выведен на новый рабочий лист (рисунок 5.3).
Рисунок 5.3 – Регрессионное уравнение
Рассмотрим рисунок 5.3. Полученное значение коэффициента детерминации R2 близко к единице, что говорит о высоком качестве уравнения – вариация независимой переменной на R2 процентов объясняется вариацией аргументов. Таблица дисперсионного анализа позволяет сравнить сумму квадратов уравнения (ячейка С12) и остаточную сумму квадратов (ячейка С13). По этим значениям рассчитывается F-критерий Фишера. Вероятность того, что полученные результаты случайны (ячейка F12) крайне низка. В практике экономических расчетов в качестве критического принят уровень в 5%.
В следующей таблице приведены коэффициенты уравнения. Их значимость проверяется с помощью t-критерия Стьюдента. Значения t-статистик для всех трех коэффициентов приведены в ячейках D17-D19. Вероятность того, что коэффициенты не значимы приведены в ячейках E17-E19. Как видим, все эти значения гораздо ниже 5%.
Итак, возьмем три коэффициента уравнения из ячеек B17, B18, B19. Теперь уравнение примет вид:
ln Y = 2.31 + 0.25 ln L + 0.75 ln K
(ln a) (1) (2)
Иными словами: ln(a) = 2.31, 1 = 0.25 и 2 =0.75. Для того, чтобы найти коэффициент a мы должны взять экспоненту: a=e ln a = e 2.31=10.07.
Таким образом, производственная функция Кобба-Дугласа имеет вид:
.
Значение F(200,100) получаем подставив эти цифры вместо K и L. Чтобы найти MRS – предельную норму замещения труда капиталом воспользуемся формулой:
Мы можем либо взять производные вручную, либо воспользоваться возможностями MathCAD. Известно, однако, что MRS для производственной функции Кобба-Дугласа равен:
,
где L и K – эластичность производственной функции по труду и капиталу соответственно.
Для производственной функции Кобба-Дугласа коэффициентами эластичности являются коэффициенты 1 и 2. Значит:
Чтобы высвободить одну единицу труда требуется ввести примерно 0.167 единиц капитала. Проверим это:
Разумеется, это относится лишь к точке (200, 100). В дальнейшем, по мере замещения труда капиталом MRSLK будет расти.
В системе MathCAD введем функцию F(L,K) и построим ее графики. Нажмем кнопку «Surface Plot» панели Graph. В появившемся прямоугольнике введем имя функции F без скобок и аргументов. График пока отображен не будет, так как по умолчанию для осей X и Y приняты интервалы, включающие отрицательные числа, что не позволяет построить функцию F. Мы должны настроить минимальное и максимальное значения. Для этого выбираем пункт «Format» контекстного меню графика. Здесь выбираем вкладку «Quick Plot Data». Для «Range 1» и «Range 2» указываем в полях «start» значение «0», как показано на рисунке 5.4. С помощью манипулятора «мышь» вращаем график так, как нам удобно. Также если удерживать клавишу Ctrl, то движение «мышью» вверх по графику «удаляет» его от наблюдателя, вниз – «приближает». Построенный нами график приведен на рисунке 5.5а. Рядом на рисунке 5.5б изображены изокванты производственной функции. Это график вида «Contour Plot», который рисуется так же, как и «Surface Plot».
Рисунок 5.4 - Вкладка «Quick Plot Data» для трехмерного графика
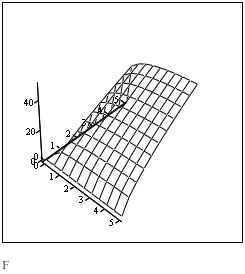
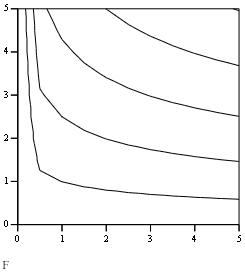
а) б)
Рисунок 5.5 – Производственная функция Кобба-Дугласа