Рекомендуемая литература по дисциплине
Бережная Е.В. Математическое методы моделирования экономических систем. Учебное пособие. - М.: Финансы и статистика, 2001.
Боков И.И. Моделирование экономических процессов. Текст лекций. Ростов-н/Д., РГЭА, 1999.
Замков О.О., Черемных Ю.А., Толстопятенко А.В. Математические методы в экономике. М.: Дело и сервис, 1999.
Интрилигатор М. Математические методы оптимизации и экономическая теория. - М.: Айрис-пресс, 2002.
Коршунов Ю.М. Математические основы кибернетики: Учебн. пособие для эконом. вузов.- М.: Энергоиздат, 1987.
Курицкий Б.Я. Поиск оптимальных решений средствами Excel 7.0. – СПб.: BHV, 1997.
Кутуков В.Б. Основы финансовой и страховой математики. –М.: Дело, 1998.
Математическая экономика на персональном компьютере / Под ред. М. Кубонива. - М.: Финансы и статистика, 1991.
Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М. Методы оптимизации. - М.: Наука, 1978.
Овчаренко Е.К., Ильина О.П., Балыбердин Е.В. Финансово-экономические расчеты в EXCEL. – М.: «Филин», 1999.
Основы теории оптимального управления: Учебн. пособие для эконом. вузов /Под ред. Кротова В.Ф. - М.: Высшая школа, 1990.
Пиндайк Р., Рубинфельд Д. Микроэкономика. - М.: Дело, 1992.
Сетевые графики в планировании. Под ред. Разумова. - М.: Высшая школа, 1975.
Терехов Л.Л. Экономико-математические методы. - М.: 1972.
Ханова А.А. Введение в систему MathCAD. - Астрахань: Изд-во АГТУ, 2001.
Четыркин Е.М. Методы финансовых и коммерческих расчетов. -М.: Дело Лтд, 1995.
Экономико-математические методы и прикладные модели: Учебн. пособие для вузов/ В.В. Федосеев, А.Н. Гармаш и др.; под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999.
Указания по выполнению лабораторных работ Лабораторная работа №1 - Решение задач линейного программирования в ms Excel Пример решения
Решим в MS Excel задачу линейного программирования.
z=x1+x2 max
Для решения задач оптимизации c помощью MS Excel нужно выполнить определенную последовательность действий.
1) Выделить диапазон ячеек для переменных х, например, A1 и B1 для х1 и х2, соответственно и ввести в эти ячейки произвольные значения (См. рисунок 1.1).
2) Ввести матрицу коэффициентов ограничений, например, в ячейки A4 и B4 вводим значения коэффициентов первого ограничения, в ячейки A5 и B6 - второго и так далее, построчно для каждого ограничения системы.
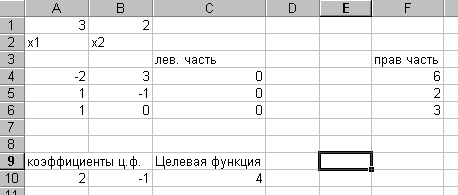
Рисунок 1.1 – Решение задачи линейного программирования
3) Рассчитать значение левых частей ограничений. Это лучше всего сделать с помощью функции СУММПРОИЗВ (диапазон; диапазон). Выбираем нужную ячейку, например, С4, затем выбираем пункт меню «Вставка -> Функция» и указываем функцию СУММПРОИЗВ(). В поле «Массив 1» вводим диапазон ячеек для переменных х (A1:B1), в поле «Массив 2» - диапазон ячеек A4:B4, содержащих значения коэффициентов 1-ого ограничения, нажимаем «OK». Аналогичным образом вводим выражения для последующих ограничений.
4) Ввести правые части ограничений, например, в ячейки F4:F6.
5) Ввести коэффициенты целевой функции, например, в ячейки А10:В10.
6) Вычислить значение целевой функции, например, в ячейку С10 с помощью функции СУММПРОИЗВ(). В поле «Массив 1» вводим диапазон ячеек для переменных х (A1:B1), в поле «Массив 2» - диапазон ячеек A4:B4, содержащих значения коэффициентов целевой функции.
7) Проверить наличие надстройки «Поиск решения», если её нет - установить с помощью пункта меню «Сервис -> Надстройки».
8) Запустить поиск решения («Сервис -> Поиск решения»). В результате получим окно, изображенное на рисунке 1.2.
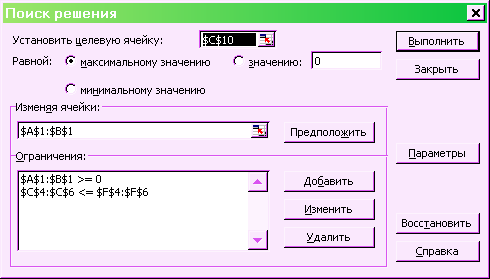
Рисунок 1.2 – Диалог «Поиск решения»
9) Указать целевую ячейку (ячейка, где лежит целевая функция, в данном случае C10) и определить, решается ли задача на минимум или максимум (в данном случае максимум).
10) Заполнить диапазон «Изменяя ячейки» - настроить на диапазон Х-ов (в данном случаеA1:B1). После выполнения диалога Excel решит задачу оптимизации и в этих ячейках будет находиться оптимальный план.
11) Добавить ограничения - сравнить левые и правые части неравенств. Нажмем кнопку «Добавить». В результате появляется окно (рисунок 1.3), куда мы и вводим новое ограничение. Здесь можно использовать интервалы, например, «$C$4:$C$6 <= $F$4:$F$6».
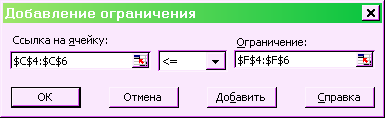
Рисунок 1.3 – Ввод ограничения
12) Задать ограничения неотрицательности ($A$1 >= 0 и $B$1 >= 0), и если нужно целочисленности описанным выше способом.
В результате выполнения получим искомые значения х в ячейках A1:B1, а также оптимальное значение целевой функции в ячейке С10.