§ 5. Решение задачи Дирихле для полупространства и полуплоскости

Пусть требуется решить задачу Дирихле для полупространства :

(1)

Возьмем в полупространстве произвольную точку и симметричную ей относительно плоскоститочку(рис. 19). Пусть- произвольная точка из полупространства . Обозначим

Легко проверить, что функция

как функция точки гармонична в полупространстве (кроме ), обращается в нуль на границе и стремится к бесконеч-ности при Значит,удовлетворяет всем необходимым требованиям и является функцией Грина поставленной задачи (1).

Вычислим . Ясно, что

, .

Положив в последней формуле и учитывая, что при этом, находим

Применив формулу (3') § 3, получим решение задачи (1)

(2)

где - плоскостьи. Преобразовав (2), получим другое представление решения задачи (1):

Аналогично решается задача Дирихле в для полуплоскости:

(3)

Пусть произвольная фиксированная точка в полуплоскости, точкасимметрична ей относительно осии- произвольная точка полуплоскости. Обозначим

Легко проверить, что функция

,

как функция точки , гармонична в полуплоскостис выколотой точкой, обращается в нуль на границе, стремится к бесконечности прии ограничена при. Значит,является функцией Грина задачи (3).

Вычислим . Из равенстванайдем

.

Применив формулу (5) § 3, получим интегральное представление решения задачи (3)

(4)

Для непрерывной и ограниченной функции интеграл (4) сходится.

Задача. Решить задачу Дирихле для полуплоскости

§ 6. Поведение производных гармонической функции на бесконечности

Пусть- гармоническая функция в неограниченной (бесконечной) области, внешней к ограниченной области. Поместим начало координат в точкувнутри областии опишем сферус центром в точкеи такого радиуса, чтолежит внутри этой сферы (рис. 20). Функциягармонична в, поэтому она гармонична вне сферыи на самой сфере. Следовательно, в области, внешней к сферефункциюможно представить по формуле Пуассона (8) § 4

(1)

где точка лежит вне сферы, точка,,.

Оценим при достаточно большом. Так как, то. Возьмем точкунастолько удаленную от начала координат, что, т.е.. Тогдаи. Поэтому, где.

Продифференцируем теперь (1) по . Получим

(2)

где . Используя приведены выше неравенства дляии замечая, чтои, получим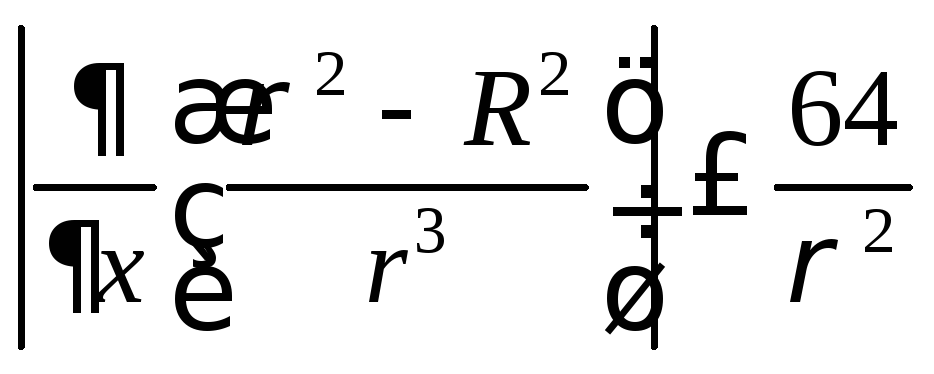. Отсюда и из (2)

Аналогично ,.

Таким образом, для гармонической в неограниченной области функции для достаточно удаленных от начала координатточекимеют место неравенства

(3)

где ,.

Из неравенств (3) следует, что функция и её первые производные приравномерно стремятся к нулю. Функции, удовлетворяющие условиям (3), называются регулярными на бесконечности.

133