§ 4. Распространение тепла на полупрямой. Операционный метод

Рассмотрим задачу о распространении тепла на полупрямой: найти ограниченную функцию , определенную при,, удовлетворяющую уравнению теплопроводности

() (1)

при граничном условии

(2)

и начальном условии

(3)

с ограниченными функциями и.

Решение задачи ищем в виде суммы , гдеи- решения следующих задач:

Первую задачу решим операционным методом, для решения второй используем результаты предыдущего параграфа.

Решим задачу . Построим изображающее уравнение по аргументу. Обозначим. Тогда,

.

Изображающее уравнение

является обыкновенным линейным дифференциальным уравнением с аргументом и параметромЕго общее решение

содержит зависящие от параметра постоянныеи. Для определениявоспользуемся предельным соотношением

Чтобы удовлетворить этому условию, следует положить . Поэтому

(4)

Для определения постоянной используем граничное условие. Введя обозначение, отсюда и из формулы (4), взятой при, получим. Таким образом

Найдем оригинал полученного изображения. Воспользуемся известными операционными равенствами и

([10], § 7). Тогда по теореме об изображении свёртки функций ([10], § 4)

К последнему интегралу применим метод интегрирования по частям. Учитывая, что внеинтегральное слагаемое обратится в нуль, получим

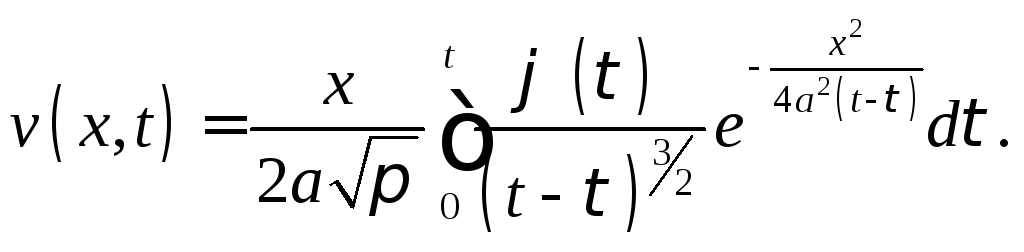
Вместо введем переменную. Тогда получим решение задачи (А):

(5)

Перейдем к решению задачи . Введем функцию

.

Из формулы (8) § 3 следует, что функция

(6)

является решением уравнения (1) и удовлетворяет начальному условию (3). Для проверки выполнимости граничного условия достаточно переписать формулу (6) в виде

(7)

При разность в квадратных скобках обращается в нуль. Таким образом, функция (7) дает решение задачи, а сумма функций (5) и (7) решает исходную задачу Коши (1) - (3).

Задача. Используя принцип Дюамеля, решить неоднородное уравнение () с граничным условием (2) и начальным условием (3).

§ 5.Распространение тепла на отрезке. Метод Фурье

Займемся решением неоднородного уравнения теплопроводности

(1)

при начальном условии

(2)

и граничных условиях

(3)

Функции ,,,предполагаются достаточное число раз дифференцируемыми.

Решение поставленной задачи разобьем на четыре этапа.

1. Рассмотрим задачу

(4)

где функция непрерывна, имеет кусочно-непрерывную производную и. Решение, согласно методу Фурье, ищем в виде. Подставив данное произведение в (4), получим. Разделим переменные:

Отсюда получаем два уравнения:

(5)

(6)

Уравнение (5) уже было подробно рассмотрено в § 3 гл. III, где было показано, что только для значений существуют нетривиальные решения

удовлетворяющие нулевым граничным условиям.

Подставив в (6), получим соответствующие решенияс произвольными постоянными. Таким образом, все функции

удовлетворяют уравнению и граничным условиям задачи (4). Составим ряд

(7)

Используя начальные условия, получим

(8)

Если коэффициенты определить равенствами

, (9)

то ряд (8) станет рядом Фурье по синусам на промежутке функции. По теореме Дирихле этот ряд равномерно и абсолютно сходится к функции.

Легко показать, что функция , определенная формулами (7) и (9), имеет производные любого порядка поив области,и, следовательно, является решением задачи (4).

2. Рассмотрим задачу

(10)

Решение ищем в виде суммы ряда Фурье

(11)

с неизвестными коэффициентами

(12)

Займемся определением функций . Дважды интегрируя (12) по частям, получим

Так как функция должна удовлетворять уравнению и граничным условиям задачи (10), то

(13)

Дифференцируя (12) по переменной , получим

(14)

Выразив интеграл из равенства (14) и подставив его в (13), получим обыкновенное дифференциальное уравнение для определения коэффициентов :

Общее решение этого уравнения

(15)

Для выполнения начального условия задачи (10) потребуем, чтобы выполнялось равенство

Отсюда

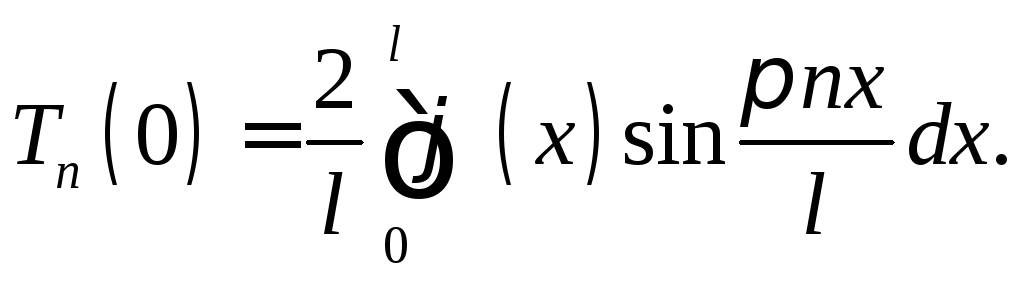(16)

Таким образом, решением задачи (10) является функция (11) с коэффициентами , определяемыми равенствами (15) и (16). Обсуждение сходимости ряда (11) и возможности его почленного дифференцирования по переменнымиоставляем читателю.

3. Рассмотрим неоднородное уравнение

(17)

с нулевыми начальными и граничными условиями

Предполагаем, что функция непрерывна, имеет кусочно-непрерывную производную пои приудовлетворяет требованиямРешение ищем в виде ряда Фурье

(18)

Ясно, что граничные условия при этом выполняются автоматически.

Предположим, что функцию , рассматриваемую как функцию аргумента, можно разложить в сходящийся к ней ряд Фурье

(19)

с коэффициентами

(20)

Формально подставив (18) и (19) в уравнение (17), получим равенство

которое должно выполняться для каждого . Это возможно только еслиявляется решением дифференциального уравнения

(21)

причем из начального условия следует, что.

Подставив решение

уравнения (21) в ряд (18), получим решение задачи (17)

(22)

Преобразуем полученное решение. Подставив в (22) выражение для из (20), получим

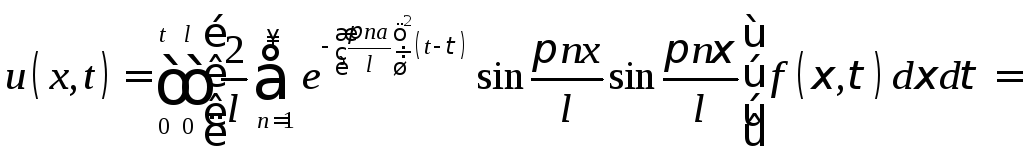
где введено обозначение

Функция называетсяфункцией Грина или функцией мгновенного точечного источника тепла. Рассматриваемая как функция аргумента функция Грина дает распределение температуры на отрезкев момент времени, порожденное действием мгновенного источника тепла, помещенного прив точке.

4. Вернемся к задаче (1) - (3), сформулированной в начале параграфа. Очевидно, что её решение является суммой функций, где- решение задачи (10),- решение задачи (17).

Задача 1. Решить задачу (1) - (3), если ,,,.

Задача 2. Методом Фурье найти решение уравнения при начальном условиии граничных условиях,.

Задача 3. Решить задачу (10) операционным методом.

Задача 4. Используя операционный метод и принцип Дюамеля, решить уравнение (17) с нулевыми начальными и граничными условиями.

Задача 5. Методом Фурье решить задачу о распределении температуры в тонкой прямоугольной пластине , при граничных условиях ,и начальном условии.

Указание. Задача сводится к решению уравнения . В соответствии с методом Фурье решение следует искать в виде. Подстановка данной функции в уравнение и разделение переменных приводит к уравнениям

, ,

с постоянными и, которые находятся из граничных условий.