Глава III. Уравнения гиперболического типа

§ 1. Теорема единственности

Решение краевых задач математической физики сводится к отысканию функции, удовлетворяющей данному уравнению и дополнительным начальным и краевым (граничным) условиям. При этом требуется, чтобы:

1) дополнительные условия были достаточны для выделения единственного решения;

2) среди дополнительных условий не было бы несовместимых.

Первое достигается доказательством теоремы единственности, второе - непосредственным нахождением решения или доказательством теоремы существования.

В качестве примера рассмотрим теорему единственности для уравнения

(1)

где . Начальные условия

(2)

В качестве граничных условий при рассмотрим любое из трех следующих:

1) граничное условие первого рода (заданный режим)

(3)

2) граничное условие второго рода (заданная сила)

(4)

3) граничное условие третьего рода (упругое закрепление)

(5)

При граничные условия задаются аналогично.

Комбинируя (3) - (5), получаем шесть типов простейших граничных условий.

Теорема (единственности). Пусть в уравнении (1) коэффициенты инепрерывны на, а функциинепрерывны прии. Тогда решение уравнения (1), удовлетворяющее начальным условиям (2) и граничным условиям, единственно.

Доказательство. Допустим, что существуют два решения и. Легко проверить, что разностьудовлетворяет однородному уравнениюи однородным начальным и граничным условиям

(6)

(7)

Докажем, что .

Рассмотрим функцию 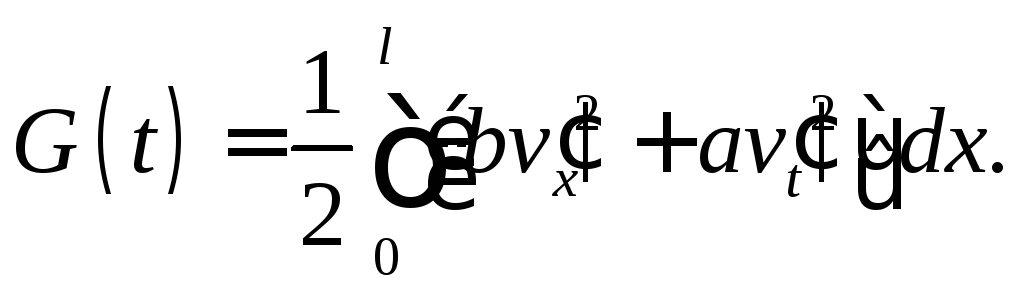Дифференцируя по, получим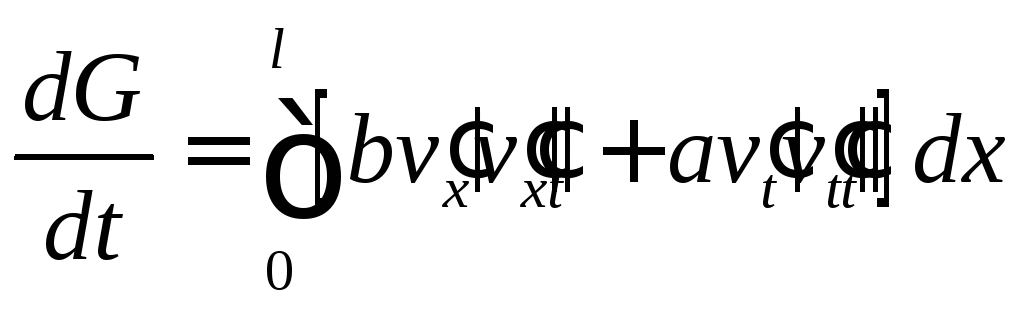. Проинтегрируем по частям первое слагаемое: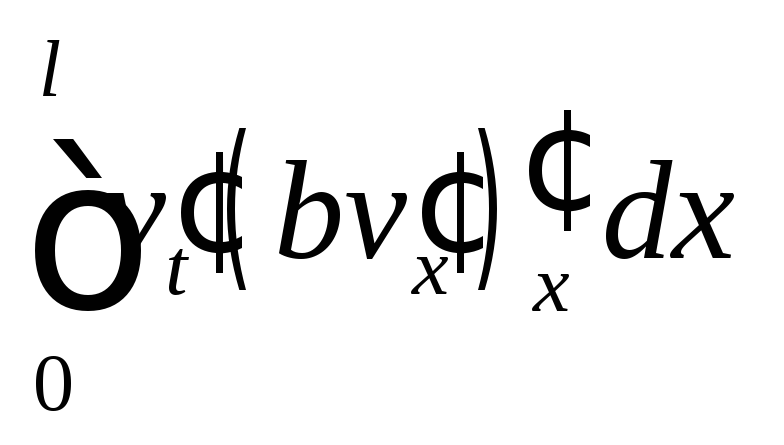. Из граничных условий (7) следует, что. Поэтому внеинтегральное слагаемое равно нулю и

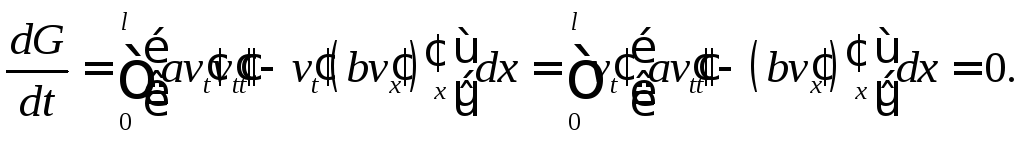
Отсюда и из начальных условий (5) следует, что

(8)

Наконец, учитывая, что коэффициенты иположительны, заключаем, что подынтегральное выражение в (8) тождественно равно нулю. Поэтомуи. Из начальных условий (6), что приводит к тождеству.■

Задача. Для уравнения (1) доказать теоремы единственности при граничных условиях второго рода (4) и третьего рода (5).

§ 2. Метод Даламбера

Неограниченная струна

Рассмотрим задачу

(1)

(2)

(), описывающую колебания неограниченной струны. Преобразуем уравнения (1) к виду, содержащему смешанную производную (гл.II, § 6, 1). Уравнение характеристикраспадается на два уравнения, общие интегралы которых. Заменаприводит (1) к виду

(3)

Найдем общий интеграл этого уравнения. Считая переменную параметром и интегрируя по, получим

где - произвольная функция переменного. Интегрируя последнее равенство по, получим

(4)

с произвольными дифференцируемыми функциями и. Так как функцияявляется решением уравнения (3) и, при соответствующем выбореи, любое решение уравнения (3) может быть представлено в виде (4), то (4) задает общий интеграл уравнения (3). Поэтому функция

(5)

является общим интегралом уравнения (1).

Определим функции итак, чтобы выполнялись начальные условия (2):

(6)

(7)

Интегрируя (7), получим 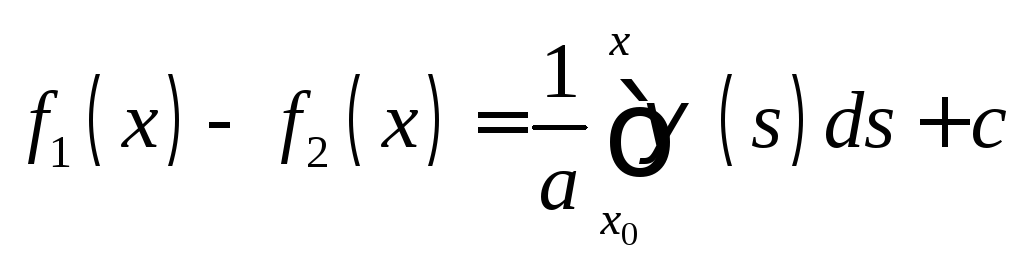, гдеипроизвольные постоянные. Отсюда и из равенства (6) находим:

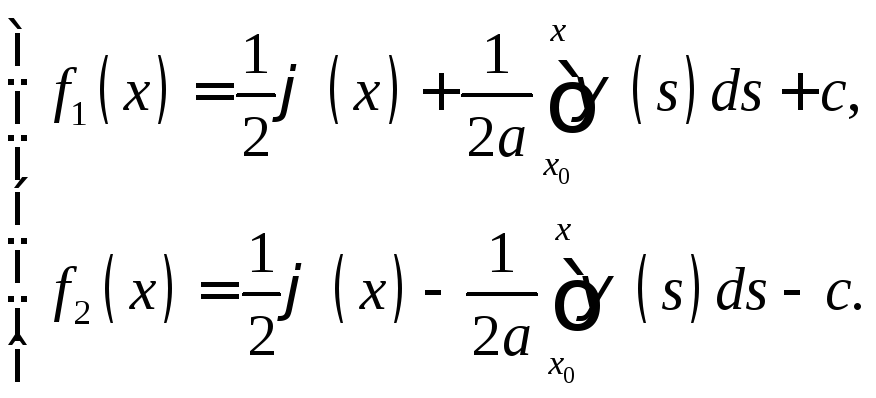(8)

Подставив найденные функции в (5), окончательно получим

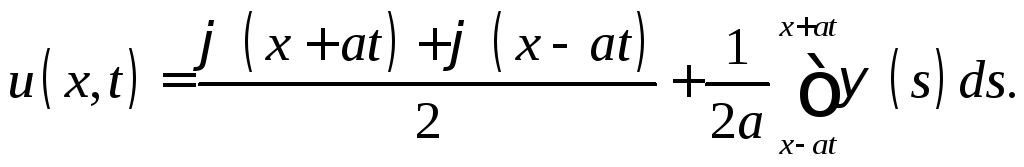(9)

Эта формула называется формулой Даламбера. Найденная функция удовлетворяет уравнению (1) и начальным условиям (2) (в предположении, что существуют производныеи).

Найденное решение имеет следующую физическую интерпретацию. Так как функции ив (5) описывают две волны, распространяющиеся соответственно в отрицательном и положительном направлениях осисо скоростью, то решение (9) является суперпозицией этих волн и описываетпроцесс распространения начального отклонения иначальной скорости (рис. 7).

Замечание. Если начальные условия не имеют нужного количества производных, то формула (9) не дает решение задачи (1) - (2). "Сгладим" начальные условия, заменив их дифференцируемыми функциями и. Тогда по формуле (9) получим решениеэтой новой задачи, которое непрерывно зависит от начальных условий. Поэтому если функциииприсходятся (в каком-либо смысле) к функциями, тосходится к функции, определенной формулой (9). Полученная таким предельным переходом функция называетсяобобщенным решением.

Пример 1. Методом Даламбера решить задачу (1) - (2), если .

Решение. Воспользовавшись формулой (9), получим решение

.

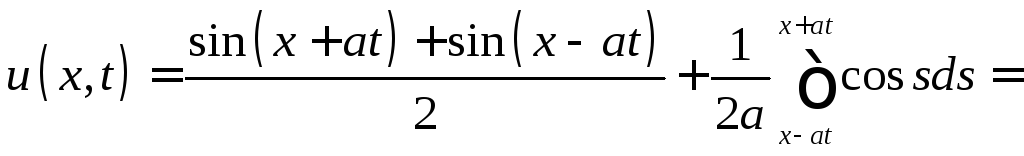
Задача 1. Методом Даламбера решить задачу (1) – (2), если

a) ;б)

Задача 2. Найти обобщенное решение задачи (1) – (2), если

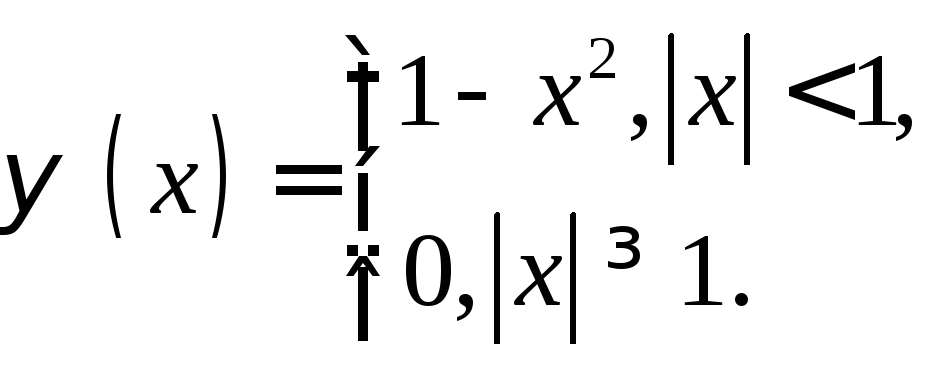
Задача 3. Для неоднородного уравнения колебаний неограниченной струны

получить формулу Даламбера ([2], с. 59)

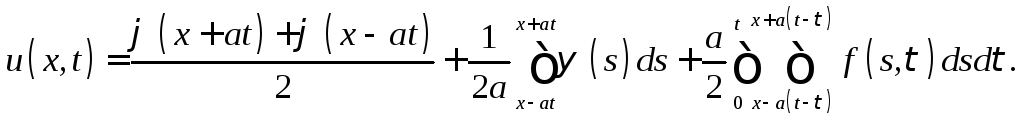
Теорема 1. Если начальное положение и начальная скорость струны в задаче (1) – (2) задаются нечетными функциями относительно какой-либо точки , то соответствующее решение в этой точке равно нулю.

Если начальное положение и начальная скорость струны в задаче (1) - (2) задаются четными функциями относительно некоторой точки , то производная посоответствующего решения в этой точке равна нулю.

Доказательство. Пусть и функцииинечетные. Тогда

и решение , определяемое формулой (9), в точкеобращается в нуль. Аналогично, если функцииичетные, то

,

так как производная четной функции является нечетной функцией и, следовательно, .■

Задача 4. Доказать, что если начальные условия задачи (1) - (2) являются четными (нечетными) функциями, то при решение (9) также обладает соответствующим свойством.

Полуограниченная струна (метод продолжения)

Рассмотрим задачу Коши

(10)

(11)

, (12)

описывающую колебания полуограниченной струны. Эта задача важна для изучения процессов отражения волн.

Введем функции

,

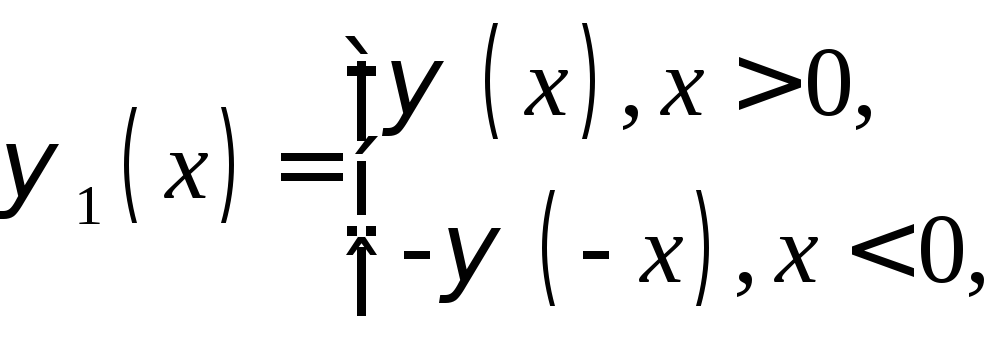
являющиеся нечетными продолжениями функций и, входящих в начальные условия (12).

Функция

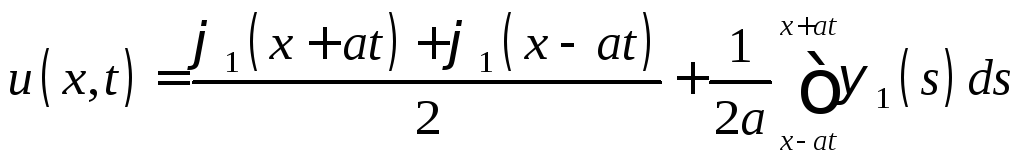
определена для всех ,, удовлетворяет начальным условиям (12) и, в силу теоремы 1, граничному условию (11). Поэтомуявляется решением задачи (10) - (12). Функция

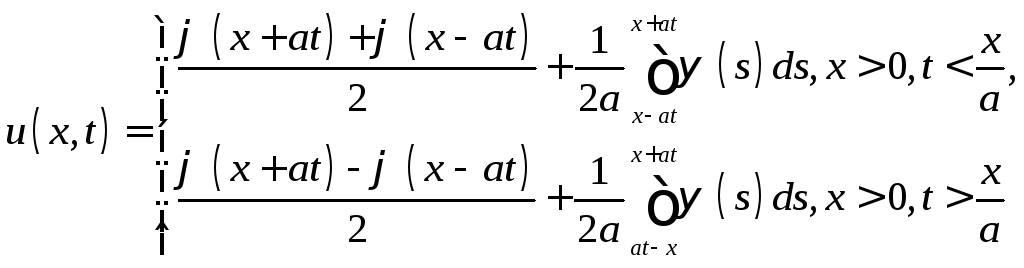
дает решение задачи (10) - (12), а также совпадает с решением (9) для бесконечной струны.

Задача 5. Изобразить процесс распространения волны, описываемой уравнением (10) и условиями (11) - (12), если , график функцииизображен на рис. 8 (штрихами изображено нечетное продолжение функциина левую полуось).

Задача 6. Используя теорему 1 доказать, что решение задачи Коши (10), (12) с граничным условием дается функцией

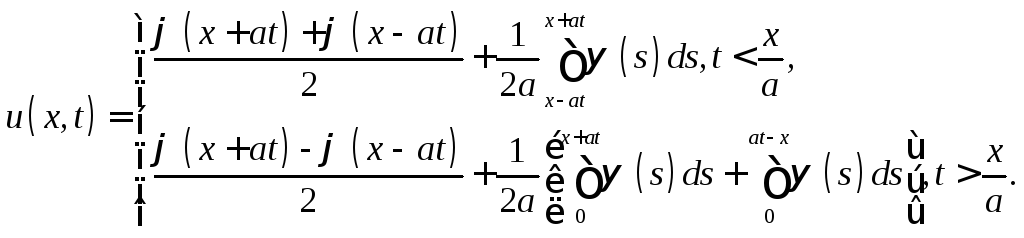
Указание. Продолжить функции ичетным образом.

Задача 7. Используя метод продолжения, решить задачу Коши для ограниченной струны длины , закрепленной на концах:

(),,.