§ 6. Задача о фазовом переходе

П

Рис. 15

остановка задачи. Рассмотрим процесс кристаллизации (замерзания) без конвекции однородного вещества с постоянной температурой фазового перехода . Предположим, что вещество заполняет полуплоскость(рис.15). Черезобозначим температуру вещества в точкев момент времениПолагаем, что в начальный моментвсё вещество имеет постоянную температуру, на границе среды и вещества (при) поддерживается постоянная температурана границе кристаллизациитемпература. Приграница кристаллизации передвигается “вглубь” вещества. Пустьтемпература в той части (фазе) вещества, через которую граница кристаллизации уже прошла,температура в оставшейся части вещества. Требуется найти распределение температуры в занимаемой веществом полуплоскости, т.е. функциии, а также закон движения границы (фронта) кристаллизации

Задача сводится к решению системы уравнений

(1)

с начальными условиями

(2)

и граничными условиями

(3)

(4)

где скрытая теплота плавления,плотность,и- коэффициенты теплопроводности и температуропроводности первой и второй фаз (все коэффициенты положительны и постоянны). Такую задачу называютзадачей Стефана, задачей Стефана-Больцмана, задачей о фазовом переходе или задачей о промерзании.

Решение. Температуру и функциюищем операционным методом. Обозначим черезизображение функции:

Изображающее уравнение

(5)

для первого из уравнений (1) является обыкновенным линейным дифференциальным уравнением второго порядка с параметром и имеет решение

где - неопределенные пока постоянные. Функцияпо условию ограничена. Поэтому изображениеограничено прии следует положить. Итак,

. (6)

Определим постоянную . Первое из граничных условий (3) дает равенство. Отсюда и из уравнения (6), в котором положим, получим. Поэтомуи изображениепримет вид

.

Найдем оригинал , соответствующий этому изображению. Воспользовавшись формулой, получим

(7)

Теперь используем (7) и второе из граничных условий (3):

. (8)

Левая часть является постоянной только тогда, когда , где- некоторая неизвестная пока постоянная. Подставив найденную функциюв (8), определим постояннуюТаким образом,

. (9)

Аналогично находим

. (10)

Постоянную найдем из граничных условий (4). Так как

,

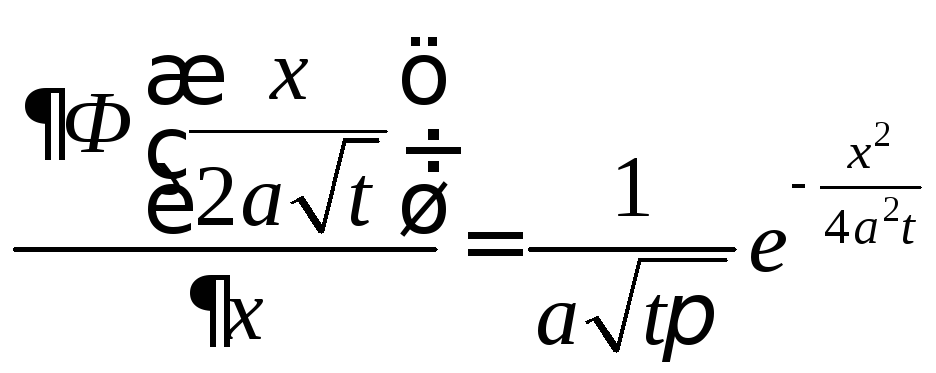то из (4) следует соотношение

. (11)

Это трансцендентное уравнение имеет единственное решение, так как при измененииот0 до левая часть монотонно изменяется отдо, а правая часть – от0 до , причем левая и правая части уравнения (11) являются непрерывными пофункциями (рис.16). Решить уравнение (11) можно численными методами. Значения функцииимеются в таблицах (см., например, [12]).

В частном случае (исходная температура вещества равна температуре кристаллизации) из уравнения (10) следует, что, уравнение (9) остается без изменений, уравнение (11) принимает вид

(12)

Обозначив ,получим уравнениегде Постоянную легко найти графически, если воспользоваться таблицами значений функцийи. Итак, приираспределение температуры задается формулой (9), прии- формулой (10). Движение фронта кристаллизацииопределяется функцией . Постояннаяявляется решением уравнения (11).

Задача 1. Проверить, что иудовлетворяют системе (1) и условиям (2)-(3).

Задача 2. Получить формулу (10).

Задача 3. Решить задачу (1)-(4) в случае .

Задача 4. Решить задачу Стефана-Больцмана (1) с начальными условиями (2) и граничными условиями (4) и

.

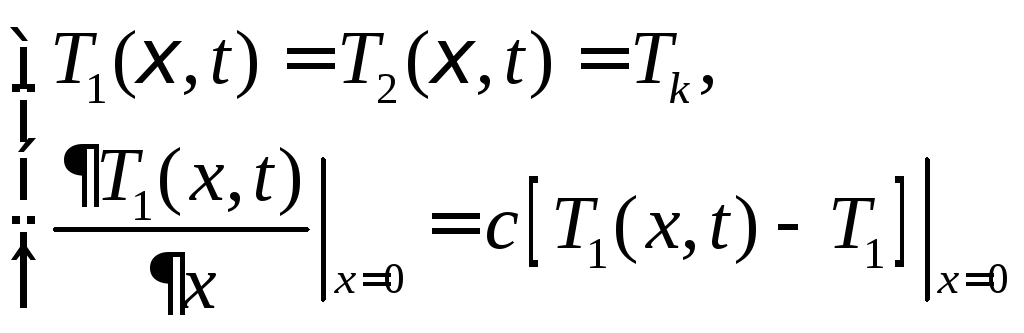Коэффициент и температура кристаллизации- заданные постоянные, причем.