§ 4. Решение задачи Дирихле для шара и круга

Пусть требуется решить внутреннюю задачу Дирихле для шара радиусас центром в точкеи поверхностью:

(1)

Из предыдущего параграфа ясно, что для решения задачи достаточно построить соответствующую функцию Грина.

Возьмем внутри шара произвольную точку и обозначим(рис. 18). Выполним преобразование инверсии относительно сферы. Образ точкиобозначим через. Ясно, что точкабудет лежать на лучевне шара на расстоянииот центра шара. Возьмем теперь произвольную точкуи обозначим,. Если точкалежит на поверхности шара, то треугольникииподобны, так как имеют общий угол при вершинеи пропорциональные стороны. Из подобия треугольников следует, чтоили

(2)

Покажем, что функция

(3)

является функцией Грина для шара. Действительно, как функция точкигармонична ввсюду кроме точки. На поверхностишара в силу соотношения (2) она обращается в нуль. Значит, удовлетворяет всем требованиям, налагаемым на функцию Грина.

Подставив найденную функцию в формулу (3') § 3, получим решение задачи (1):

(4)

Преобразуем полученную формулу. Из равенств

следует, что

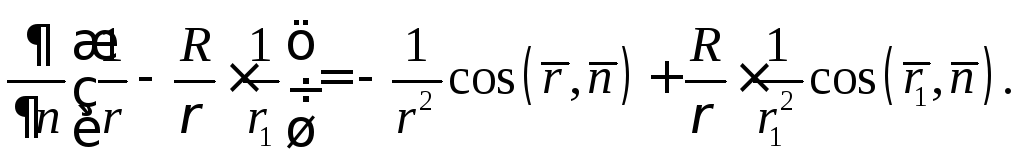(5)

По теореме косинусов из треугольников иимеем

Выразим отсюда ии подставим их в (5). С учетом полученных ранее равенствиполучим

Подставив в формулу (4), получим формулу Пуассона

(6)

Таким образом, если решение внутренней задачи Дирихле (1) для шара существует, то оно представимо по формуле (6).

Существование решения задачи (1) определяется следующей теоремой.

Теорема 1 ([1], гл. 19, § 6). Если функция непрерывна, то решение задачи Дирихле (1) для шара существует и определяется формулой (6).

Задача 1. Доказать теорему 1.

Задача 2. Доказать, что задача (1) корректна, если функция непрерывна.

Получим другой вид формулы Пуассона (6). Введем сферическую систему координат с центром О в центре сферы. Пусть - координаты точки,- координаты точкии- угол, образованный векторамии. Тогда формулу (6) можно записать в виде

(7)

Совершенно аналогично строится функция Грина для области, внешней к сфере радиусас центром в точке. При этомрешение внешней задачи Дирихле для шара дается формулой Пуассона

(8)

где ,, точка. В сферических координатах формула (8) приобретает вид

(9)

где - сферические координаты точки,- сферические координаты лежащей на сфереточки,- угол, образованный векторамии.

Задача 3. Построить функцию Грина внешней задачи Дирихле для шара и получить формулы (8) и (9).

Функция Грина задачи Дирихле для круга получается тем же способом, что и для сферы. Только в этом случае функцию Грина следует искать в виде

с гармонической в круге функцией (см. § 3). Повторяя рассуждения, проведенные в начале параграфа, получим функцию Грина в виде

(10)

(обозначения те же, что на рис. 18). Легко проверить, что определенная таким образом функция гармонична в кругерадиусаи обращается в нуль на границе. Поэтому решение внутренней задачи Дирихле для уравнения Лапласа в кругес границей

(11)

дается формулой (5) § 3:

(12)

Вычисление на окружностиприводит к равенству

(13)

Подставив (13) в (12), получим формулу Пуассона

, (14)

дающую решение задачи (11).

Если в правой части (14) добавить множитель -1, получим решение внешней задачи Дирихле (11) для круга.

Задача 4. Провести необходимые вычисления и получить функцию (10) и формулу (14).

Задача 5. Решить внутреннюю задачу Дирихле для круга -граница круга,Аи Впостоянные.