Глава IV. Уравнения параболического типа

Уравнения параболического типа, простейшим из которых является уравнение теплопроводности , возникают при изучении процессов теплопередачи, движения вязкой жидкости, диффузии и в ряде других случаев. В данной главе доказаны теоремы существования и единственности решения уравнений параболического типа для ограниченных и неограниченных областей и рассмотрены основные методы решения краевых задач для однородных и неоднородных уравнений: методы разделения переменных с применением рядов и интегралов Фурье, метод точечного источника, операционный метод, комбинированные методы. Приведено решение задачи о фазовом переходе.

§ 1. Принцип максимума

Пусть тело не содержит источников тепла. Предположим, что на его границеи в начальный момент в каждой внутренней точкетела температура не превосходит некоторой величины. Тогда вполне очевидно, что с течением времени внутри тела не может возникнуть температура, большая. Теорема, содержащая чёткую формулировку этого утверждения, носит названиепринцип максимума. Займемся её формулировкой и доказательством.

В евклидовом пространстве рассмотрим цилиндр, основанием которого является ограниченная областьТочкапространствапринадлежит цилиндру, если,Образующие цилиндра параллельны осинижнее основаниесоответствует значениюверхнее - значениюТу часть границы цилиндра, которая состоит из нижнего основанияи боковой поверхности, обозначим через, границу областиобозначим через.

Теорема 1 (принцип максимума). Если функция удовлетворяет уравнению теплопроводности

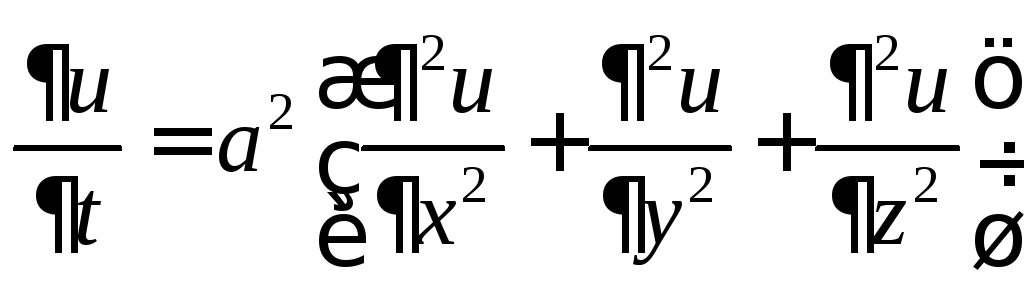(1)

внутри цилиндра Q и непрерывна в , то максимальное и минимальное значения она принимает на поверхностиФ.

Доказательство. 1) Если , то утверждение теоремы выполняется - функция достигает своего максимального (минимального) значения в любой точке цилиндра, в том числе и на его границе.

2) Утверждение о минимуме функции сводится к утверждению о максимуме функции, поэтому докажем лишь утверждение о максимальном значении. Доказательство проведем методом от противного. Обозначим

.

Предположим, что теорема неверна, т.е. существует такое решение , для которого. Пусть значениепринимается во внутренней точкецилиндраили приРассмотрим функцию

где - диаметр области. Ясно, чтоа на поверхности

Значит, функция не принимает наибольшего значения ни на боковой поверхности, ни на нижнем основании цилиндра. Пусть её максимум достигается в точке, причем точкалежит внутри, а. Тогда в этой точке производные,,неположительные,приипри. Поэтому в точкевыполняется неравенство

С другой стороны

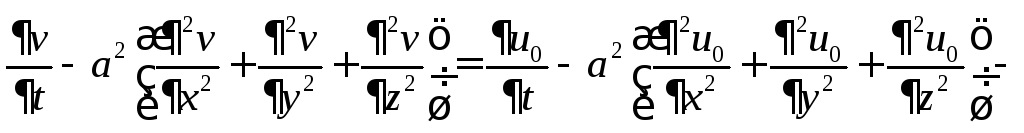
Получено противоречие, значит .■

Замечание. Принцип максимума имеет место для областей любой конечной размерности.

Задача 1. Сформулировать и доказать принцип максимума для ограниченных областей в пространствах двух и трех измерений.

Рассмотрим теперь следующую задачу: в цилиндре найти решение уравнения (1), удовлетворяющее начальному условию

(2)

и граничному условию

(3)

Функции ипредполагаются непрерывными.

Из принципа максимума вытекают следующие утверждения.

Теорема 2. Решение задачи (1) - (3) в цилиндре единственно.

Доказательство. Допустим, что имеются два различных решения и. Тогда функцияудовлетворяет уравнению (1) и обращается в нуль прии на поверхностиобласти. Из принципа максимума тогда следует, что.■

Теорема 3. Решение задачи (1) - (3) в цилиндре непрерывно зависит от начальных и граничных условий.

Доказательство. Пусть - решение уравнения (1), удовлетворяющее условиям (2) - (3), а- решение уравнения (1), отвечающее возмущенным начальным и граничным условиями. Предположим, что возмущенияимало отклоняются от нуля,,. Тогда разностьявляется решением уравнения (1), удовлетворяющим малым граничным и начальным условиям, и по принципу максимума во всех точках цилиндратакже по абсолютной величине не превосходит.■

Задача 2. Перенести теоремы 2 и 3 на неоднородное уравнение теплопроводности.

Задача 3. Пусть решения иуравнения теплопроводности

, ,(4)

удовлетворяют условиям . Доказать, чтопри всех значениях,.

Задача 4. Доказать, что если три решения ,,уравнения (4) удовлетворяют условиямпри,и, то эти же неравенства выполняются тождественно при всех,.