§ 8. Колебания нити

Задача о малых колебаниях под действием силы тяжести тяжелой однородной нити длины , закрепленной в точке(рис. 14), сводится к интегрированию уравнения

(1)

с граничным условием

(2)

и начальными условиями

(3)

Замена приведет уравнение (1) к виду

(4)

Решение ищем методом Фурье. Положив

(5)

подставив (5) в (4) и разделив переменные, придем к уравнению

.

Приравняв каждую из полученных частей к постоянной, значение которой определим позднее, получим два уравнения:

(6)

(7)

Замена преобразует уравнение (6) в уравнение Бесселя

(8)

с постоянной . Согласно результатам, полученным в предыдущем параграфе, общее решение уравнения (8) имеет вид

Так как , то следует положитьи решение уравнения (6) искать в виде.

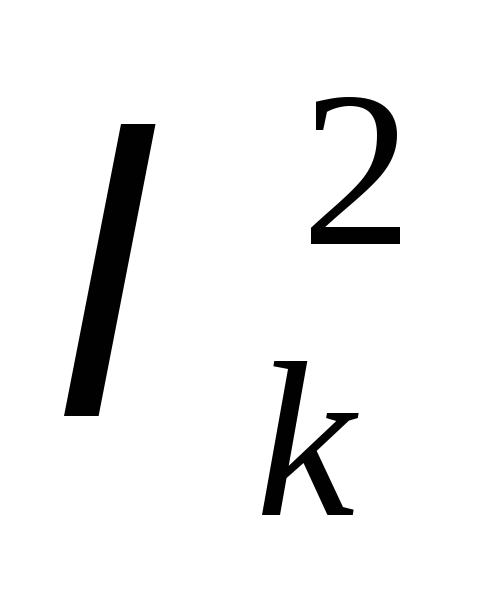Граничное условие дает равенство . Из асимптотического равенства (9) § 7 и свойств функций Бесселя следует, что уравнениеимеет счетное множество положительных корней, причем. Поэтому значенияпостоянной(собственные числа задачи Штурма – Лиувилля) определяются равенствами

. (9)

Собственные функции , отвечающие этим собственным числам, имеют видили, после возвращения к переменной,

(10)

Перейдем к уравнению (7). Подставив вместо 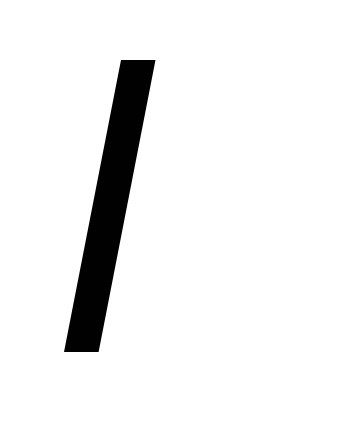найденные значения из (9), получим общие решения уравнения (7), отвечающие каждому из чисел:

Поэтому в соответствии с методом Фурье формула

(11)

дает общее решение уравнения (1), удовлетворяющее граничному условию (2).

Теперь определим постоянные итак, чтобы решение (11) удовлетворяло начальным условиям (3). Положив в (11)и подставив полученный ряд в (3), получим разложение функции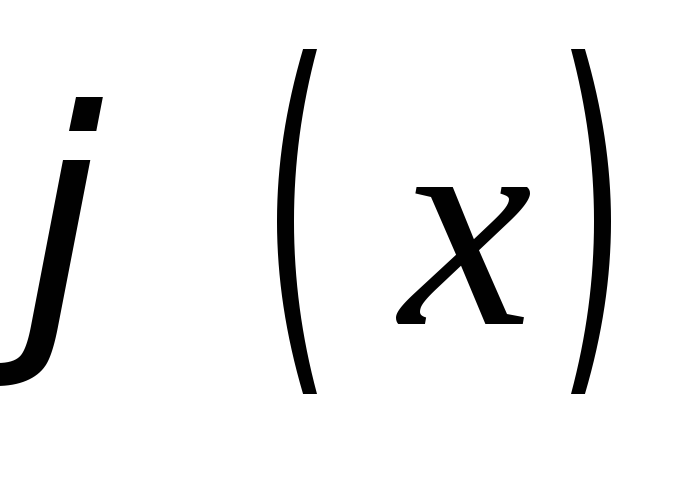в ряд Фурье-Бесселя

(12)

Для определения коэффициентов умножим обе части равенства (12) наи почленно проинтегрируем по отрезку:

(13)

Выполним в каждом из интегралов, стоящих под знаком суммы, замену и воспользуемся свойством ортогональности функций Бесселя (формула (11) § 7):

Подставив найденное значение интеграла в формулу (13), найдем коэффициенты :

(14)

Используя второе начальное условие (3) и рассуждая аналогично, найдем коэффициенты :

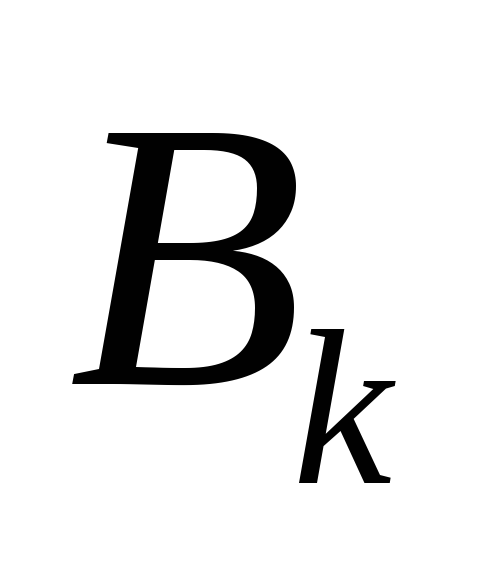(15)

Итак, функция , определенная рядом (11), коэффициенты которого вычисляются по формулам (14) и (15), дает решение поставленной задачи о малых колебаниях тяжелой нити. Легко убедиться, что колебания подвешенной нити складываются из бесконечного набора гармонических колебаний.

Задача. По аналогии с задачей о колебаниях струны (§ 3) найти частоты, основной тон и узловые точки подвешенной колеблющейся нити.

87