
§ 3. Метод Фурье
Метод
Фурье
или метод
разделения переменных
является одним из основных методов
решения уравнений с частными производными.
Изложим суть метода на примере задачи
о колебании струны длины
![]() ,
закрепленной на концах.
,
закрепленной на концах.
Колебания струны описываются уравнением
![]()
![]()
![]() (1)
(1)
граничные условия
![]() (2)
(2)
начальные условия
![]()
![]() (3)
(3)
Решение
ищем в виде произведения
![]() ,
где
,
где![]()
![]() функция переменного
функция переменного![]() ,
,![]()
![]() - функция переменного
- функция переменного![]() .
Подставив
.
Подставив![]() в (1) и поделив на
в (1) и поделив на![]() получим равенство
получим равенство![]() ,
где точками обозначена вторая производная
по
,
где точками обозначена вторая производная
по![]() ,
штрихами – вторая производная по
,
штрихами – вторая производная по![]() .
Левая часть этого равенства зависит
только от
.
Левая часть этого равенства зависит
только от![]() ,
правая – только от
,
правая – только от![]() .
Для того, чтобы равенство выполнялось
тождественно для всех
.
Для того, чтобы равенство выполнялось
тождественно для всех![]() и
и![]() ,
потребуем, чтобы каждая из его частей
была постоянной. Обозначим эту постоянную
через
,
потребуем, чтобы каждая из его частей
была постоянной. Обозначим эту постоянную
через![]() .
Получим обыкновенные дифференциальные
уравнения
.
Получим обыкновенные дифференциальные
уравнения
![]()
![]() , (4)
, (4)
![]()
![]() (5)
(5)
с граничными условиями
![]()
![]() .
.
Отсюда
следует, что
![]() .
.
Граничная задача отыскания нетривиального решения уравнения
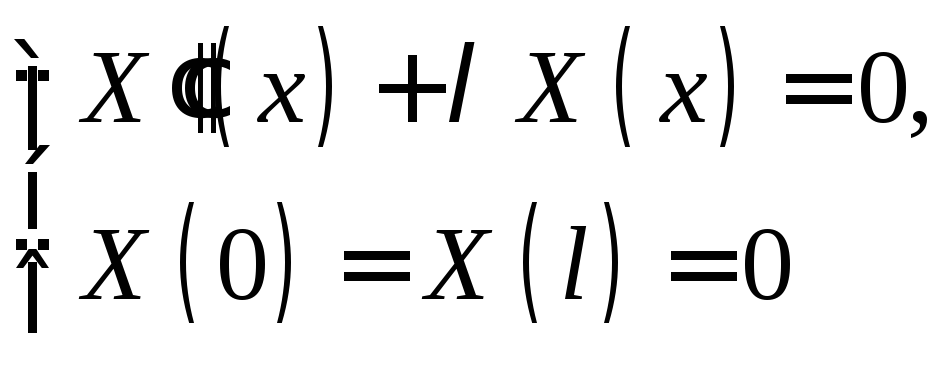 (6)
(6)
и
тех значений параметра
![]() ,
при которых это решение существует,
называется задачей Штурма – Лиувилля,
числа
,
при которых это решение существует,
называется задачей Штурма – Лиувилля,
числа![]() - собственными числами (собственными
значениями), решения – собственными
функциями задачи.
- собственными числами (собственными
значениями), решения – собственными
функциями задачи.
Рассмотрим все возможные случаи.
1)
Если
![]() ,
то
,
то![]() и из граничных условий следует, что
и из граничных условий следует, что![]() ,
т.е.
,
т.е.![]() .
.
2)
Если
![]() ,
то
,
то![]() .
Поэтому
.
Поэтому![]() .
Граничные условия снова приводят к
равенствам
.
Граничные условия снова приводят к
равенствам![]() и
и![]() .
.
3)
Если
![]() ,
то
,
то![]() .
Граничные условия дают равенства
.
Граничные условия дают равенства![]() ;
;![]() .
Так как
.
Так как![]() ,
то
,
то![]() .
Следовательно
.
Следовательно![]() ,
откуда
,
откуда![]() (
(![]() - любое натуральное число). Таким образом,
ненулевые решения возможны только при
- любое натуральное число). Таким образом,
ненулевые решения возможны только при![]() .
Этим собственным числам отвечают
собственные функции
.
Этим собственным числам отвечают
собственные функции
![]()
Подставив
найденные числа
![]() в (5), получим набор решений уравнения
(5)
в (5), получим набор решений уравнения
(5)
![]() (7)
(7)
с
произвольными постоянными
![]() и
и
![]() .
.
Возвращаясь к задаче (1) – (3) заключаем, что функции
![]() (8)
(8)
являются частными решениями уравнения (1) и удовлетворяют граничным условиям (2). Уравнение (1) линейно и однородно, поэтому формальная сумма частных решений
![]() (9)
(9)
также
(формально) удовлетворяет этому уравнению
и граничным условиям (2). Остается
подобрать коэффициенты
![]() и
и![]() так, чтобы функция (9) удовлетворяла
начальным условиям (3). Формально подставив
(9) в (3), получим систему
так, чтобы функция (9) удовлетворяла
начальным условиям (3). Формально подставив
(9) в (3), получим систему
 (10)
(10)
Из
теории рядов Фурье известно ([5], гл.VII,
§ 11), что в силу теоремы Дирихле
кусочно-непрерывная и кусочно-дифференцируемая
функция
![]() ,
заданная на отрезке
,
заданная на отрезке![]() ,
раскладывается в ряд Фурье
,
раскладывается в ряд Фурье
![]()

Полагая,
что функции
![]() и
и![]() этим условиям удовлетворяют, получим
этим условиям удовлетворяют, получим
![]()
 (11)
(11)
![]()
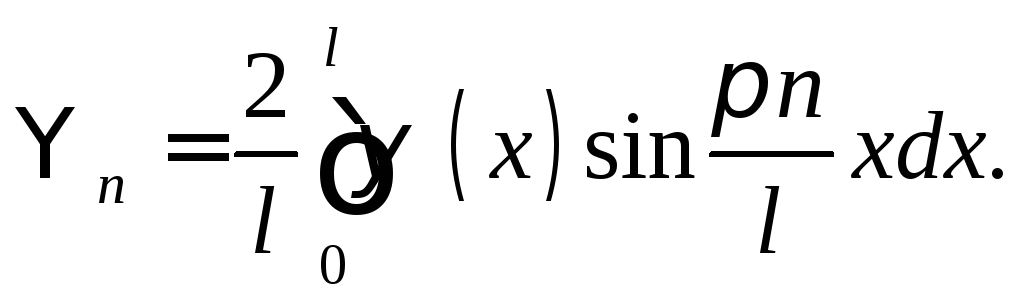 (12)
(12)
Подставив
(11) и (12) в (10) и используя условие равенства
двух тригонометрических рядов, получим
![]() ,
,![]() .
Таким образом, функция
.
Таким образом, функция
![]() (13)
(13)
дает формальное решение задачи (1) - (3).
Замечание
1.
Формальное решение (13) становится
"настоящим" решением, если ряд (13)
и ряды для производных
![]()
![]()
![]() ,
полученные из (13) почленным дифференцированием,
сходятся. В [13, 22] доказано, что для этого
достаточно, чтобы функции
,
полученные из (13) почленным дифференцированием,
сходятся. В [13, 22] доказано, что для этого
достаточно, чтобы функции![]() ,
,![]() и
и![]() были непрерывными, функции
были непрерывными, функции![]() и
и![]() - кусочно-непрерывными и
- кусочно-непрерывными и![]()
![]() .
Эти условия не являются необходимыми
и связаны только с выбранным методом
решения. При решении задачи методом
Даламбера (§ 2) и операционным методом
(§ 5) условия, накладываемые на функции
.
Эти условия не являются необходимыми
и связаны только с выбранным методом
решения. При решении задачи методом
Даламбера (§ 2) и операционным методом
(§ 5) условия, накладываемые на функции![]() и
и![]() ,
менее ограничительные.
,
менее ограничительные.
Замечание 2. Решение задачи о колебании струны, записанное в форме тригонометрического ряда (13), позволяет проанализировать физические свойства этого процесса.
Запишем решение (13) в виде
![]()
где
![]() ,
,![]() .
Отсюда видно, что колебание струны
слагается из отдельных гармонических
колебаний
.
Отсюда видно, что колебание струны
слагается из отдельных гармонических
колебаний
![]()
причем
колебание каждой точки
![]() происходит с одной и той же амплитудой
происходит с одной и той же амплитудой![]() и частотой
и частотой![]() .
Такое движение струны называетсястоячей
волной.
Точки
.
Такое движение струны называетсястоячей
волной.
Точки
![]()
![]() ,
в которых амплитуда равна нулю, остаются
неподвижными и называютсяузлами
стоячей волны
,
в которых амплитуда равна нулю, остаются
неподвижными и называютсяузлами
стоячей волны
![]() .
Точки
.
Точки![]()
![]() ,
в которых
,
в которых![]() и амплитуда
и амплитуда![]() максимальная, называютпучностями
стоячей волны (рис. 9). Частоты
максимальная, называютпучностями
стоячей волны (рис. 9). Частоты
![]() называютсобственными
частотами
колебаний струны.
называютсобственными
частотами
колебаний струны.
Легко
подсчитать энергию
![]() -
й гармоники (
-
й гармоники (![]() -
й стоячей волны):
-
й стоячей волны):
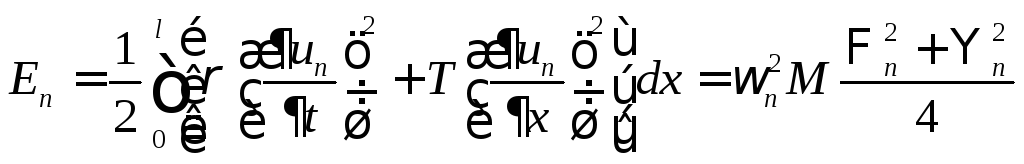
(![]() -
масса струны,
-
масса струны,![]() -
постоянная плотность,
-
постоянная плотность,![]() ).
).
З вук,
издаваемый колеблющейся струной,
является "смесью" звуков,
соответствующих стоячим волнам.Тон,
или высота, и сила звука зависят от
частоты и амплитуды колебаний. Самый
низкий тон определяется собственной
частотой
вук,
издаваемый колеблющейся струной,
является "смесью" звуков,
соответствующих стоячим волнам.Тон,
или высота, и сила звука зависят от
частоты и амплитуды колебаний. Самый
низкий тон определяется собственной
частотой
![]() и называетсяосновным
тоном струны.
Остальные тона, соответствующие частотам
и называетсяосновным
тоном струны.
Остальные тона, соответствующие частотам
![]() ,
кратным
,
кратным![]() ,
называютсяобертонами
и характеризуют "окраску" звука,
его тембр.
Энергия основного тона, вообще говоря,
больше энергии других тонов. Она зависит
от начальных условий (3), чем широко
пользуются при проектировании музыкальных
инструментов.
,
называютсяобертонами
и характеризуют "окраску" звука,
его тембр.
Энергия основного тона, вообще говоря,
больше энергии других тонов. Она зависит
от начальных условий (3), чем широко
пользуются при проектировании музыкальных
инструментов.
Подробнее с теорией звука можно познакомиться по книгам [24, 25].
Задача
1.
Методом Фурье решить неоднородное
уравнение колебаний струны
![]() с начальными и краевыми условиями (2),
(3).
с начальными и краевыми условиями (2),
(3).
Задача
2.
Найти решение задачи (1) – (3) в виде ряда
Фурье по произвольной полной
ортонормированной на
![]() системе функций
системе функций![]()
![]() .
.
Метод Фурье применим не только к уравнениям второго порядка.
Задача
3.
Методом Фурье решить уравнение поперечных
колебаний стержня
![]() с граничными условиями
с граничными условиями![]() ,
,![]() ,
,![]() и начальными условиями
и начальными условиями![]() ,
,![]()
![]() .
.
