§ 5. Операционный метод

Операционное исчисление дает еще один метод решения волновых уравнений. Например, если искомая функция является функцией двух аргументов, то по одному аргументу можно построить изображающее уравнение, которое будет уже обыкновенным дифференциальным уравнением относительно второго аргумента. Интегрируя полученное уравнение, находят изображение искомого решения, а затем и само решение [10]. Если искомая функция является функцией трех аргументов, удобно применять двойное преобразование Лапласа [25].

Решим операционным методом уравнение поперечных колебаний струны

, (1)

с граничными условиями

(2)

и начальными условиями

(3)

Построим для (1) изображающее уравнение по аргументу . Обозначим . Тогда

,

Поэтому изображающее уравнение для уравнения (1) имеет вид

и является обыкновенным линейным дифференциальным уравнением второго порядка относительно аргумента с параметром.

Общее решение этого уравнения ищем обычным методом:

В силу граничных условий поэтому . Аналогично

поэтому

Таким образом, изображением искомого решения служит функция

Заметив, что полюсами функции являются только корни уравнения , т.е. числа , причем все полюсы простые, оригинал найдем по обобщенной теореме разложения ([10], § 2):

Числа оказываются коэффициентами ряда Фурье функции при разложении ее по синусам на отрезке :

Задача 1. Найти решение уравнения (1) с граничными условиями (2) и начальными условиями

.

Задача 2. Найти решение уравнения (1) с граничными условиями (2) и начальными условиями

.

§ 6. Формула Пуассона

В предыдущих параграфах были приведены различные методы решения волнового уравнения, в котором искомая функция являлась функцией двух аргументов - пространственной переменнойи времени. Теперь рассмотрим волновое уравнение в пространстве:

(1)

Ищем решение, удовлетворяющее начальным условиям

(2)

причем функция предполагается непрерывной вместе со всеми производными до третьего порядка, а- до второго порядка включительно. Граничные условия отсутствуют.

Теорема 1. Пусть произвольная дважды непрерывно дифференцируемая вфункция,- сфера радиусас центром в точке. Тогда функция

(3)

дает решение уравнения (1).

Доказательство. Координаты точек сферывыразим равенствамигде- косинусы углов, образованных радиусами сферыи координатными осями. Когда точкадвижется по сфере, точкадвижется по сфереединичного радиуса. Элементы площадейиэтих сфер связаны равенствами, поэтому интеграл (3) можно записать в виде

(4)

По условию функция дважды непрерывно дифференцируема, поэтому функциятакже имеет дважды непрерывно дифференцируемые производные. Найдем вторые производные по, сложим и возвратимся к исходной области интегрирования. Получим

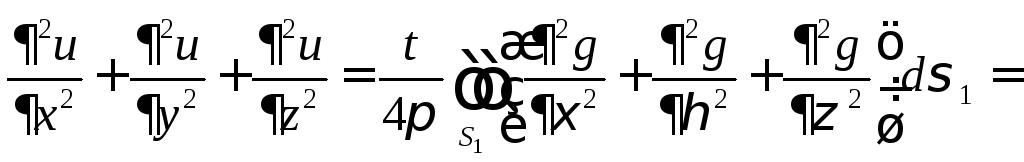
(5)

Дифференцируя функцию (4) по , получим

(6)

С учетом (4) отсюда следует равенство

Применив к последнему интегралу формулу Остроградского, получим

где - шар с поверхностью. Обозначим последний интеграл черезТогда

Дифференцируя по , получим

(7)

Вычислим производную . Для этого перейдем в интегралек сферическим координатамс центром в точке. Тогда

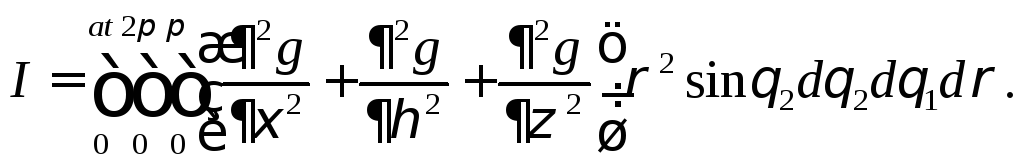
Продифференцируем последний интеграл по . Учитывая, что, получим

(8)

Теперь утверждение теоремы следует из формул (5), (7) и (8). ■

Следствие 1. Из формул (4) и (6) следует, что функция , определенная формулой (3), удовлетворяет начальным условиям

(9)

Следствие 2. Пусть - решение уравнения (1), определенное формулой (3) и удовлетворяющее начальным условиям (9), и пусть функцияимеет непрерывные производные до третьего порядка включительно. Легко установить, что функциятакже является решением уравнения (1), удовлетворяющим начальным условиям

(следствие формулы (6)),

(10)

Из (3), (9) и (10) теперь следует, что функция

(11)

дает решение задачи Коши (1)–(3). Формула (11) называется формулой Пуассона.

Приведем картину распространения в пространстве волн, описываемую формулой Пуассона. Предположим, что начальное возмущение сосредоточено в части пространства , ограниченной поверхностью(рис. 12). Это значит, что функциии, задающие начальные условия, равны нулю вне области. Пустьи- расстояние произвольной точкипространства до ближайшей и наиболее удаленной точексоответственно. Приобластьнаходится вне сферы, функцииина сфере равны нулю и по формуле (11) имеем. Это означает, что начальное возмущение еще не успело дойти до точки. Начиная с моментадо моментасферабудет пересекать область, поверхностные интегралы в (11) станут, вообще говоря, отличными от нуля, и точкаперейдет в возбужденное состояние. Моментамисоответствует прохождение через точкупереднего и заднего фронта волны. Фронт волны - это поверхность, разделяющая колеблющиеся и неподвижные точки. При сфераохватит область, поверхностные интегралы в (11) снова станут равными нулю и точкавозвратится в состояние покоя. Последействие отсутствует.

Ясно, что постоянная является скоростью распространения фронта волны.

Замечание 1. Рассмотрим частный случай задачи (1) - (3), когда функции ине зависят от. Очевидно, что при этом правая часть формулы (11) также не будет зависеть оти формула даст решение волнового уравнения

(12)

с начальными условиями

(13)

В трехмерном пространстве уравнения (12) - (13) описывают цилиндрические волны. Преобразуем формулу (11) для этого случая.

Пусть точка М является центром сферы , лежит в плоскостиOxy и имеет координаты . Обозначим черезкруг с центром в точкеМ радиуса , являющийся проекцией сферына плоскостьOxy. По формуле (4) § 2 гл.1 преобразуем поверхностные интегралы, содержащиеся в формуле (11), в двойные интегралы по области . Обозначив черезугол между осьюOz и нормалью в произвольной точке сферы , получим

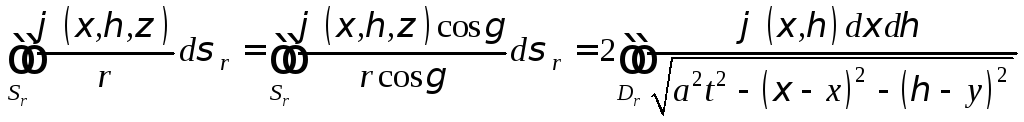
(множитель 2 перед последним интегралом появляется вследствие того, что интегралы по верхней и по нижней полусферам сферы равны).

Аналогично преобразовав второй интеграл в (11), получим формулу Пуассона, решающую задачу (12)-(13) для плоскости:

Если функции изависят только от одной переменной, то формула Пуассона преобразуется в формулу Даламбера (9) § 2 для волнового уравнения с одной пространственной переменной.

Отметим, что на плоскости в случае локализованного начального возмущения возникает волна, которая имеет передний фронт, но не имеет заднего фронта. Этим плоские волны принципиально отличаются от волн, распространяющихся в пространстве.

Замечание 2. Решение волнового уравнения в случае областей, ограниченных плоскостями, можно искать методом отражения. Например, рассмотрим в полупространстве уравнениес начальными условиями

и граничным условием илиЕсли начальные условия продолжить на все пространство нечетно по(при)

,

или четно (при )

то формула Пуассона (11) даст решение поставленной задачи.

Аналогично решается задача для плоского слоя при граничных условиях первого родаили второго рода

Замечание 3. Формула Пуассона содержит под знаками интегралов функции и, определяющие начальные условия и достаточное количество раз непрерывно дифференцируемые. Поэтому при конечныхмалые изменения начальных условий влекут малые изменения решения, т.е.решение задачи Коши (1) - (3) непрерывно зависит от начальных данных

Задача 1. Решить задачу (1)-(2), если а начальные отклоненияимеют вид:

a)

б)

Так как функция не обладает нужным количеством производных, получитьформальное решение.

Задача 2. Решить задачу (12)-(13), если а начальные отклоненияимеют вид:

a)

б)