5.3. Геометрическое распределение.

Говорят, что случайная величина X имеет геометрическое распределение, если её возможные значения 0,1,2,…,m,…,а вероятности этих значений:

(5.3.1)

где 0p1; q=1-p; m=0,1,2…

Дисперсия с.в. X

D_x=q/p² (5.3.7)

И с.к.о.

(5.3.8)

На практике чаще приходится рассматривать не с.в. Х, имеющую геометрическое распределение, а другую с.в.:

Y=X+1 (5.3.9)

(число попыток до первого «успеха», включая удавшуюся).

Ряд распределения с.в. Y имеет вид:

Y:	1	2	3	…	m	…
	p	qp	q2p	…		…

Будем называть такое распределение «геометрическим, сдвинутым на единицу» или «геометрическим +1».Многоугольник распределения с.в. Y при p=0,4 имеет тот же вид, что и на рис. 5.3.1, но сдвинут вправо на одну единицу (рис. 5.3.2).

Найдём м.о. и дисперсию с.в. Х. Пользуясь свойствами числовых характеристик, приведёнными в п. 4.2, получим

(5.3.10)

(5.3.11)

(5.3.12)

6.2. Показательное распределение.

Говорят, что непрерывная с.в. Х имеет показательное (или «экспоненциальное») распределение, если

или, короче,

(x0). (6.2.1)

Положительная величина  называется параметром показательного распределения. График показательного распределения показан на рис. 6.2.1. Его функция распределения:

(x0).

График ф.р. показательного распределения показан на рис. 6.2.2.

Найдём числовые характеристики показательного распределения:

Производя интегрирование по частям и учитывая, что при x e^-x стремится к нулю быстрее, чем возрастает любая степень x, находим

(6.2.2)

т.е. м.о. случайной величины, имеющей показательное распределение, обратно его параметру  (который имеет размерность, обратную размерности с.в. Х).

Вычислим дисперсию с.в. Х по формуле:

(6.2.3)

Отсюда с.к.о.

(6.2.4)

т.е. с.к.о. с.в. Х, имеющей показательное распределение, равно её м.о.:

Коэффициент вариации с.в. Х, имеющей показательное распределение (6.2.1), равен единице:

(6.2.5)

Коэффициент вариации, показывающий, какую долю математического ожидания составит с.к.о., служит своего рода характеристикой «степени случайности» неотрицательной случайной величины и в ряде случаев применяется для её оценки. Случайные величины, имеющие 1 – «более случайны».

Чтобы найти асимметрию показательного распределения, найдём его третий центральный момент:

Откуда коэффициент асимметрии

Как и следовало ожидать, асимметрия показательного распределения положительна.

Показательное распределение тесно связано с простейшим (стационарным пуассоновским) потоком событий. Интервал времени Т между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром, равным интенсивности потока:

(t0). (6.2.6)

6.3. Нормальное распределение.

Нормальный закон распределения (иногда называется законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Говорят, что с.в. Х распределена по нормальному закону с параметрами m, ,если её плотность распределения имеет вид:

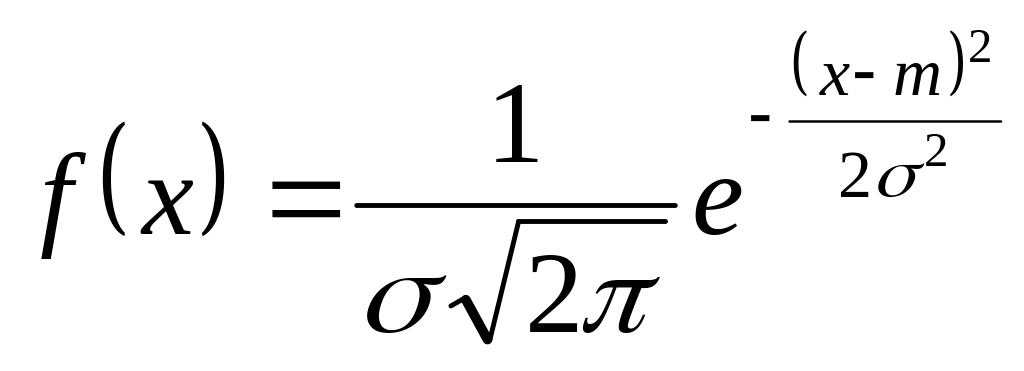(6.3.1)

или, пользуясь весьма удобным способом записи показательной функции ехр{x}=e^x (она позволяет избегать «многоэтажных» формул),

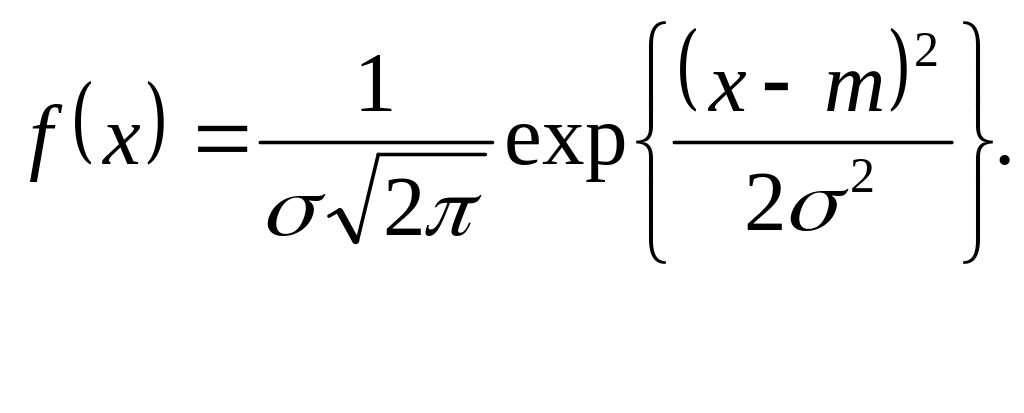(6.3.1)

Кривая нормального распределения имеет симметричный, холмообразный вид (рис.6.3.1).

Максимальная ордината кривой, равная 1/ достигается при x=m (мода M_x=m); из соображений симметрии мы вправе ожидать, что она совпадает с м.о. случайной величины Х, ели оно существует (ниже мы непосредственно в этом убедимся). По мере удаления от точки m плотность f(x) падает, и при x кривая распределения асимптотически приближается к оси абсцисс.

Посмотрим, как будет меняться кривая распределения при изменении параметров m, . При изменении m кривая f(x),не изменяя своей формы, просто будет смещаться вдоль оси абсцисс. Изменение  равносильно изменению масштаба кривой по обеим осям; например, при удвоении  масштаб по оси абсцисс удвоится, а по оси ординат- уменьшится в два раза. Для иллюстрации на рис. 6.3.2 показаны три нормальные кривые распределений; для всех трёх m=0; для кривой (I) =1, для кривой (II) =2,5,для кривой (III) =1/2 (при построении кривых мы пользовались таблицей значений функции

- нормальная плотность для m=0, =1, приведённой в приложении [4].

Вычислим для нормальной с.в. Х вероятность попадания на участок от  до :

Как известно, неопределённый интеграл не выражается через элементарные функции, но его можно выразить через специальную функцию

(6.3.15)

называемую функцией Лапласа (или «интегралом вероятностей»), для которой составлены таблицы (приложение 2)*).

С помощью этой функции вероятность попадания нормально распределённой с.в. Х на участок от  до  выражается простой формулой:

(6.3.16)

Функция Лапласа Ф(х) обладает следующими свойствами: 1) Ф(0)=0; 2) Ф(-х)=-Ф(х) (нечётная функция); 3) Ф(+)=0,5 (и, значит, Ф(-)=-0,5).

Наиболее просто выражается через функцию Лапласа вероятность попадания нормально распределённой с.в. Х на участок длиной 2l, симметричный относительно центра рассеивания (рис.6.3.3). А именно,

или, принимая во внимание нечётность функции Лапласа,

(6.3.17)

Через функцию Лапласа выражается и ф.р. F(x) нормально распределённой с.в. Х. По формуле (6.3.16), полагая =-, =x и учитывая, что Ф(-)=-1/2, получим:

(6.3.18)