4.2. Моменты. Дисперсия. Среднее квадратическое отклонение.

Кроме характеристик положения, в теории вероятностей употребляется ещё ряд числовых характеристик различного назначения; каждая из них характеризует случайную величину с точки зрения тех или иных особенностей её распределения. Среди них особое значение имеют моменты – начальные или центральные.

Начальным моментом s-го порядка случайной величины X называется математическое ожидание s-й степени этой величины:

(4.2.1)

Для дискретной случайной величины X начальный момент s-го порядка выражается суммой:

(4.2.2)

где x_i – значения случайной величины X, p_i – соответствующие вероятности; для непрерывной – интегралом:

(4.2.3)

где f(x) – плотность распределения.

Выражения (4.2.2) и (4.2.3) и их обобщение (4.2.4) мы здесь записали без специального доказательства, считая их естественными; сомневающиеся могут найти вывод выражения для математического ожидания любой функции случайной величины в п. 8.1.

Ранее введённая характеристика положения – математическое ожидание с. в. – есть не что иное, как её первый начальный момент

(4.2.5)

Перед тем, как дать определение центральных моментов, введём новое понятие «центрированной случайной величины». Центрированной случайной величиной называется отклонение случайной величины от её математического ожидания:

(4.2.6)

Условимся отличать центрированную с.в. значком наверху. Нетрудно убедиться, что м.о. центрированной с.в. равно нулю:

;

аналогично и для непрерывной.

Центрирование случайной величины, очевидно, равносильно переносу начала отсчёта в точку m_x (центр распределения).

Моменты центрированной случайной величины называются центральными моментами. Они аналогичны моментам относительно центра массы в механике.

Центральным моментом порядка s с.в. X называется м.о. s-й степени центрированной с.в.:

. (4.2.7)

Для дискретной с.в. центральный момент выражается суммой:

(4.2.8)

для непрерывной – интегралом:

(4.2.9)

В дальнейшем, в тех случаях, когда не возникает сомнений, о какой с.в. идёт речь, мы будем для краткости вместо и писать просто и .

Очевидно для любой с.в. X центральный момент 1-го порядка равен нулю:

. (4.2.10)

Между центральными и начальными моментами существует связь: одни выражаются через другие. Выведем соответствующие формулы для дискретной случайной величины (для непрерывных вывод будет аналогичным при замене на , на , сумм на интегралы) Второй центральный момент:

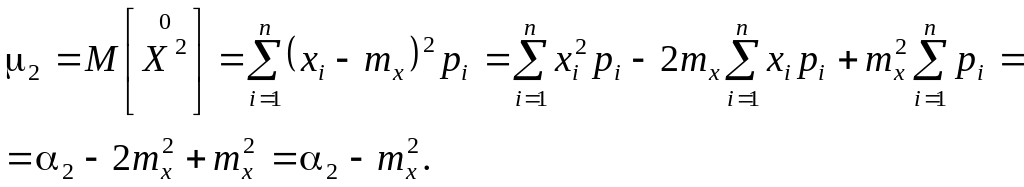
Особое значение для практики имеет второй центральный момент . Он называется дисперсией с.в. Ввиду крайней важности этой характеристики среди других, введём для неё специальное обозначение или кратко :

Согласно определению центрального момента:

(4.2.12)

т.е. дисперсия случайной величины есть математическое ожидание квадрата соответствующей центрированной величины.

Для непосредственного вычисления дисперсии служат формулы

(4.2.13)

(для дискретной с.в.);

(4.2.14)

(для непрерывной с.в.)

На практике часто бывает проще вычислить второй начальный момент, чем дисперсию; тогда пользуются выражением последней через (вторая из формул (4.2.11)):

(4.2.16)

или в других обозначениях:

(4.2.17)

т.е. дисперсия случайной величины равна математическому ожиданию её квадрата минус квадрат математического ожидания. Эту формулу полезно запомнить.

Дисперсия имеет размерность квадрата случайной величины, что не всегда удобно; для наглядности в качестве характеристики рассеивания удобнее пользоваться числом, размерность которого совпадает с размерностью с.в. Для этого из дисперсии извлекают квадратный корень. Полученная величина называется средним квадратическим отклонением (иначе «стандартом» или «стандартным отклонением») случайной величины. Будем обозначать его [Х] (или _х):

(4.2.18)

Корень берётся его арифметическим, т.е. положительным значением. Для упрощения записей мы часто будем пользоваться сокращением для среднего квадратического отклонения (или просто , если ясно, о какой с.в. идёт речь). Вместо слов «среднее квадратическое отклонение» будем иногда писать с.к.о.

Для неотрицательной случайной величины X в качестве характеристики «степени её случайности» иногда применяется коэффициент вариации, равный отношению с.к.о.к.м.о.:

=/m (4.2.19)

Зная м.о. и с.к.о. случайной величины X, можно составить себе приближённое представление о диапазоне её возможных значений. А именно, значения случайной величины X только изредка выходят за пределы интервала

(4.2.20)

и в большинстве случаев можно считать, что они укладываются в этот интервал. Это правило (оно более строго будет обосновано в дальнейшем, п. 10.2 гл. 10) носит название «правила трёх сигма». Согласно этому правилу для того, чтобы приближённо представить себе размах случайных отклонений с.в. X от её м.о., достаточно отложить от точки m вправо и влево по отрезку, равному 3 (рис.4.2.1).

Математическое ожидание m, дисперсия D (или с.к.о. ) – чаще всего применяемые числовые характеристики с.в. Они характеризуют самые важные черты распределения: его положение и степень разбросанности. Для более подробного описания распределения служат моменты высших порядков. Третий центральный момент ₃ служит для характеристики асимметрии («скошенности») распределения. Если распределение симметрично относительно м.о. (или, в механической интерпретации, относительно центра массы), то все центральные моменты нечётного порядка (если они существуют) равны нулю. Действительно, при симметричном распределении и нечётном s в сумме

каждому положительному слагаемому соответствует равное ему по абсолютной величине отрицательное слагаемое, так что они взаимно уничтожаются и сумма равна нулю (то же справедливо и относительно интеграла, выражающего _s для нечётного s, который равен нулю как интеграл в симметричных пределах от нечётной функции). Естественно поэтому в качестве характеристики асимметрии распределения выбрать какой-либо из нечётных моментов – проще всего ₃. Он имеет размерность куба случайной величины; чтобы получить безразмерную характеристику, делят её на куб с.к.о. Полученная величина носит название «коэффициента асимметрии» или просто «асимметрии» (иначе – «скошенности»); её обозначают Sk (от английского skew – «косой»):

Sk=₃/³. (4.2.21)

На рис. 4.2.2 изображены две асимметричных кривых распределения f₁(x), f₂(x); одна из них (I) имеет положительную асимметрию (Sk0), вторая (II) – отрицательную (Sk0).

Четвёртый центральный момент ₄ служит для характеристики так называемой «крутости», т.е. островершинности или плосковершинности распределения ( применяется в основном к непрерывным с.в.). Это свойство характеризуется с помощью так называемого эксцесса:

(4.2.22)

Число 3 вычитается из отношения ₄/⁴ потому, что для весьма распространённого и часто встречающегося нормального распределения (о нём будет идти речь в гл. 6 и далее) отношение ₄/⁴=3. Для нормального распределения _x =0; кривые, более островершинные, чем нормальная, обладают положительным эксцессом, более плосковершинные – отрицательным (рис. 4.2.30). Характеристикой _x пользуются главным образом для симметричных распределений.

Из определения м.о. и дисперсии следуют некоторые простейшие и достаточно очевидные свойства этих числовых характеристик.

1) Математическое ожидание неслучайной величины c равно самой c:

.

(Действительно, если с.в. X имеет только одно значение c с вероятностью 1, M[c]=c1=c).

2) Дисперсия неслучайной величины c равна нулю:

.

3) При прибавлении к с.в. X неслучайной величины c к её м.о. прибавляется та же величина:

.

(это свойство достаточно наглядно следует из механической интерпретации м.о. как центра массы).

4) При прибавлении к с.в. X неслучайной величины c её дисперсия не меняется:

Действительно, при прибавлении к с.в. X неслучайной величины та же неслучайная величина c прибавляется к её м.о., а центрированная с.в. не меняется (это же наглядно следует из механической интерпретации дисперсии как момента инерции относительно центра массы).

В частности, из свойства 4 следует, что при центрировании случайной величины её дисперсия не меняется.

5) При умножении с.в. X на неслучайную величину c на ту же величину c умножается её м.о.:

(это свойство достаточно наглядно следует из того, что при умножении на c масштаб по оси 0x также множится на c).

6) При умножении с.в. X на неслучайную величину c её дисперсия множится на c²:

Действительно, каждое значение с.в. множится на c, на то же c множится её м.о. и каждое и каждое значение центрированной с.в. ; её квадрат множится на c², на то же c² множится и дисперсия:

7)Извлекая корень, получим:

т.е. при умножении с.в. X на неслучайную величину c её с.к.о. множится на модуль этой неслучайной величины.