34

Теория надежности изучает процессы возникновения отказов технических объектов и способы борьбы с отказами.

АСУ ТП – автоматизированная система управления технологическим процессом.

Элемент – составная часть системы.

Состояния объектов бывают:

1. работоспособное;

2. неработоспособное.

ГОСТ 13377-75: Состояние объекта, при котором он способен выполнять заданные функции, сохраняя значение заданных параметров в пределах, установленных нормативно-технической документацией (НТД), называют работоспособным.

Состояние объекта, при котором значение хотя бы одного заданного параметра, характеризующего способность выполнять заданные функции, не соответствующие требованиям, установленным НТД, называется неработоспособным.

Отказ – событие, заключающееся в нарушении работоспособности, то есть в переходе в неработоспособное состояние.

Неработоспособность – состояние, при котором нельзя выпускать объект в эксплуатацию. Возможны и другие признаки неработоспособного состояния – объект требует капитального ремонта и прочее. Поэтому при оценке надежности необходимо оговорить, какое состояние считается неработоспособным.

Когда объект предназначен для выполнения нескольких функций, часто приходится находить показатели надежности по каждой из функций.

Возможен и другой путь: оценивают возможность объекта выполнять все требуемые от него функции. Отказом считается невыполнение хотя бы одной независимо от того, возникла ли она случайно или нет.

Иногда на практике встречаются такая постановка задачи теории надежности. В этом случае при оценке надежности учитывают случайную потребность в выполнении объектом отдельных функций.

Пусть система, состоящая из п элементов, которые предназначены для выполнения к функций. Функционирование такой системы может быть представлено как процесс изменения вектора состояний Z(t) в пространстве состояний [x(t), y(t)], где х_i – состояние i-го элемента системы, i=1,2,…,п; у_j – переменная, характеризующая потребность в выполнении j функции, j=1,2,…,k.

Обычно предполагается, что отдельные координаты вектора Z(t) являются независимыми случайными функциями времени наработки, принимающими одно из двух возможных значений:

Искомые показатели надежности находят как числовые характеристики некоторого функционала от случайного процесса Z(t). Понятие функционала является обобщение понятия функции. Функционал Ф определен на процессе Z(t), если каждой траектории ставится в соответствие некоторое число

В рассматриваемом случае найденные показатели надежности характеризуют не техническую систему, а ситуацию по удовлетворению случайного спроса.

Виды отказов объектов:

1. По характеру устранения.

Окончательные (устойчивые) являются следствием необратимых процессов в деталях и материалах. Для восстановления работоспособности необходимо производить ремонт оборудования (отказ телевизора из-за лампы накаливания).

Перемежающиеся (то возникающие, то появляющиеся). Как правило, являются следствием обратимых случайных изменений режимов работы и параметров объекта. При возвращении в нормальный режим работы объект сам возвращается в работоспособное состояние. Следствия перемежающихся и окончательных отказов резко отличаются. Это зависит от области использования, от общих показателей системы. Следовательно, показатели надежности отличаются для окончательных и перемежающихся отказов.

2. По связи с другими отказами.

Первичные, то есть возникающие по любым причинам, кроме действия другого отказа.

Вторичные, возникающие в результате другого отказа.

Отказы являются случайными событиями, которые могут быть зависимыми и независимыми. Отказы являются зависимыми, если при появлении одного из них изменяется вероятность появления второго отказа. Для независимых отказов вероятность появления одного из них не зависит от того, произошли другие отказы или нет. Различие между вторичными и зависимыми отказами состоит в том, что после появления первичного отказа вторичный отказ другого элемента наступает неизбежно, а для зависимого отказа лишь изменяется вероятность его появления.

3. По легкости обнаружения.

Очевидные (явные) и скрытые (неявные).

4. По внешним проявлениям.

Терминология и классификация зависят от области применения (обрыв, замыкание и т.д.).

5. По характеру возникновения.

Внезапные – мгновенное изменение характеристик объекта (грубые отказы; не имеют видимых признаков).

Постепенные – медленное, постепенное ухудшение качеств объектов (связаны с износом, старением материалов и разрегулированием устройств).

Объекты, различающиеся показателями и методами оценки надежности:

1. Неремонтируемые объекты, применимые до первого отказа;

2. Ремонтируемые объекты, восстановление которых в процессе применения невозможно (невосстанавливаемые объекты);

3. Ремонтируемые восстанавливаемые в процессе применения объекты, для которых недопустимы перерывы в работе;

4. Ремонтируемые, восстанавливаемые в процессе применения объекты, для которых допустимы кратковременные перерывы в работе.

Рис. 1. Группы объектов, различающиеся показателями надежности.

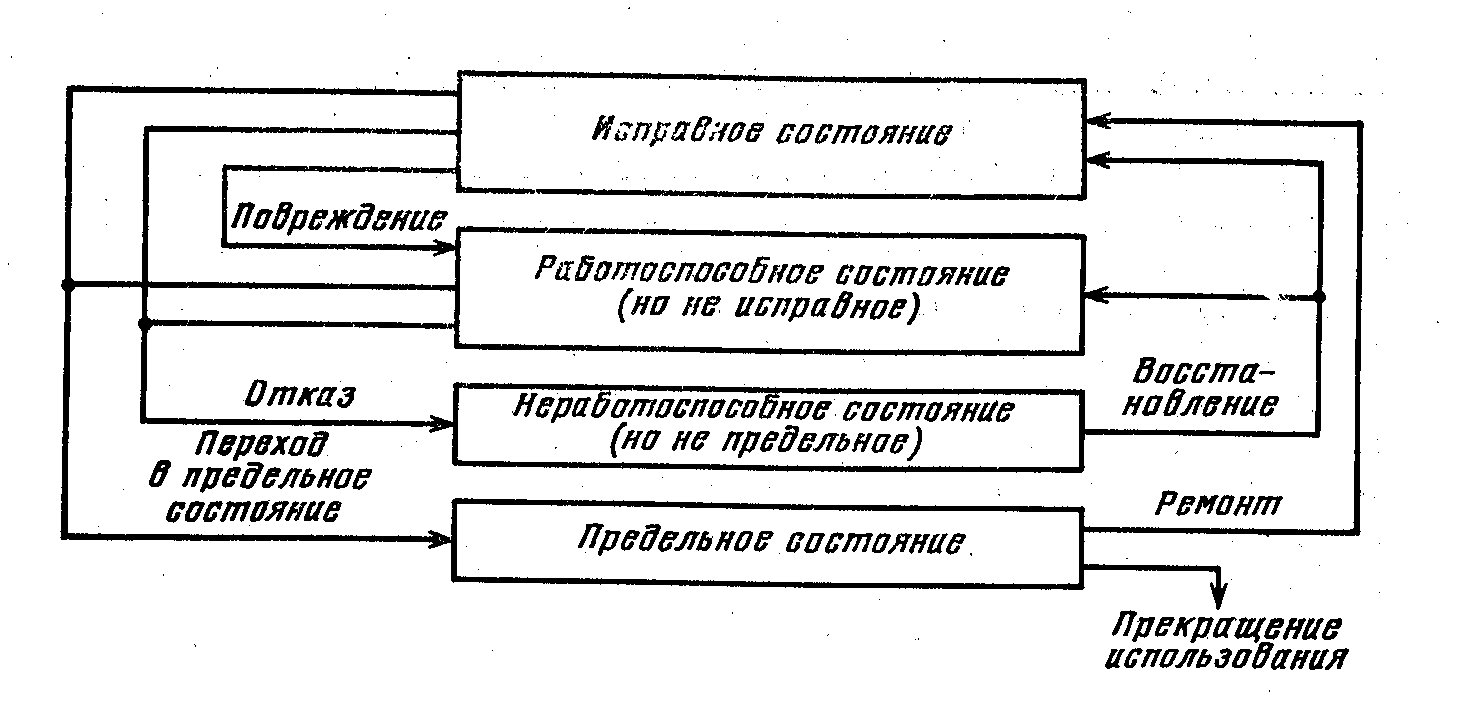
Схема основных состояний и событий восстанавливаемой системы

Основные понятия теории вероятности

Случайное событие. Его вероятность .

Любая наука, развивающая общую теорию какого-либо круга явлений, содержит ряд основных понятий, на которых она базируется. Таковы, например, в геометрии понятия точки, прямой, линии; в механике — понятия силы, массы, скорости, ускорения. Естественно, что не все основные понятия могут быть строго определены, ибо «определить» понятие — это значит свести его к другим, более известным. Очевидно, процесс определения одних понятий через другие должен где-то кончаться, дойдя до самых первичных понятий, к которым сводятся все остальные и которые сами не определяются, а только поясняются. Такие понятия существуют и в теории вероятностей. Здесь мы рассмотрим некоторые из них.

Под опытом (экспериментом, испытанием) мы будем понимать некоторую воспроизводимую совокупность условий, в которых наблюдается то или другое явление, фиксируется тот или другой результат, Заметим, что «опыт» не обязательно должен быть поставлен человеком; он может протекать независимо от него; при этом человек выступает в роли наблюдателя или фиксатора происходящего. От него зависит только решение: что именно наблюдать и какие параметры фиксировать.

Если результат опыта варьируется при его повторении, говорят об опыте со случайным исходом. Именно такие опыты мы будем здесь рассматривать и добавление «со случайным исходом» для краткости опускать. Тот факт, что при повторении опыта его основные условия сохраняются, и, значит, мы вправе ожидать устойчивости частот, тоже не будем каждый раз оговаривать.

Случайным событием (или, короче, просто событием) называется всякий факт, который в опыте со случайным исходом может произойти или не произойти. События мы будем обозначать большими буквами латинского алфавита.

Рассмотрим несколько примеров событий. 1. Опыт — бросание монеты; событие А - появление герба.

2. Опыт - бросание трех монет; событие В - появление трех гербов.

3. Опыт - передача группы из и сигналов по каналу связи; событие С - искажение хотя бы одного из них.

4. Опыт - выстрел по мишени; событие D - попадание.

5. Опыт - вынимание наугад одной карты из колоды; событие Е - появление туза.

6. Тот же опыт, что в примере 5; событие F - появление карты червонной масти.

7. Опыт (наблюдение) - измерение количества осад- ков, выпадающих в данном географическом пункте за определенный месяц; событие G - выпадение более N миллиметров осадков.

8. Опыт - лечение группы больных определенным препаратом; событие Н - существенное улучшение более чем у половины из них.

Все приведенные примеры, начинались с описания опыта, в котором появляется или не появляется событие. В общем случае это необязательно; опыт может упоминаться после формулировки события; например: А - появление герба при бросании монеты; В - появление трех гербов при бросании трех мо нет и т. д.

Рассматривая перечисленные в наших примерах события А, В, ..., Н, мы видим, что каждое из них обладает какой-то степенью возможности — одни большей, а другие меньшей, причем для некоторых из них мы сразу можем решить, какое из них более, а какое менее возможно. Например, сразу видно, что событие А более возможно (вероятно), чем В, а событие F более возможно, чем Е. Относительно других событий нашего списка таких выводов сразу сделать нельзя; для этого условия опыта описаны недостаточно подробно. Так или иначе, любое случайное событие обладает какой-то степенью возможности, которую в принципе можно измерить численно. Чтобы сравнивать между собой события по степени их возможности, нужно связать с каждым из них какое-то число; которое тем больше, чем более возможно событие. Это число мы и назовем вероятностью события.

В основе применения всех выводов и рекомендаций, добываемых с помощью теории вероятностей, лежит принцип практической уверенности, который может быть сформулирован следующим образом:

Если вероятность события А в данном опыте весьма, мала, то (при однократном выполнении опыта) можно вести себя так, как будто событие А вообще невозможно, т. е. не рассчитывать на его появление.

Обратим внимание на слова «при однократном выполнении опыта» в формулировке принципа практической уверенности. Дело в том, что производя много опытов, в каждом из которых вероятность события А ничтожно мала, мы повышаем вероятность того, что событие А произойдет хотя бы один раз в массе опытов. В самом деле, представьте себе лотерею, в которой на миллион билетов всего один выигрыш. Некто покупает один билет. Вероятность выигрыша для него 0,000001, т. е. ничтожно мала, и можно считать выигрыш практически невозможным. А теперь представьте себе, что распроданы все 1000000 билетов. Кто-то из купивших получит выигрыш, т. е. для него произойдет практически невозможное событие. За счет чего? За счет того, что опыт (покупка билета) произведен очень много раз.

Аналогично обстоит дело с надежностью сложных агрегатов. Пусть агрегат состоит из большого числа N элементов. Каждый из них отказывает (выходит из строя) с ничтожно малой вероятностью. Но за счет того, что элементов очень много, вероятность того, что откажет хотя бы один из них, перестает быть близкой к нулю (см. пример 16 п. 2.4).

Переходим к самому тонкому и трудному вопросу: насколько мала должна быть вероятность события, чтобы его можно было считать практически невозможным?

Ответ на этот вопрос выходит за рамки математической теории и в каждом отдельном случае решается из практических соображений, в соответствии с той важностью, которую имеет для нас желаемый результат опыта. Чем опаснее возложенная ошибка предсказания, тем ближе к нулю должна быть вероятность события, чтобы его считать практически невозможным.

Например, когда мы, на основе вероятностных расчетов, предсказываем, что средний результат N взвешиваний не отклонится от истинного веса тела больше, чем на заданную величину е, а вероятность того, что отклонение будет больше е, равна 0 01, мы еще можем примириться с этим и считать событие А - «ошибка больше » - практически невозможным. Чем мы в данном случае рискуем? Легкой неправильностью предсказания.

Совершенно другое дело - если вероятность взрыва космической ракеты при ее запуске равна тем же 0,01. Риск велик, велика ответственность; в таких условиях, во что бы то ни стало надо добиваться «вероятности неудачи» на несколько порядков меньшей.

Размер допустимой «вероятности риска» всегда назначается исследователем, исходя из степени опасности риска. Выбирается он более или менее произвольно. Поэтому на всех прогнозах, осуществляемых методами теории вероятностей, всегда лежит отпечаток «начального произвола», связанного с выбором достаточно малой «вероятности риска», — вероятности того, что прогноз не оправдается. Это обстоятельство отнюдь не снижает ценности вероятностных методов исследования. «Ориентировочный прогноз» все же лучше, чем «никакой прогноз», который вытекал бы из требования, чтобы «вероятность риска» была в точности равна нулю.

Непосредственный подсчет вероятностей

Для всякого опыта, обладающего симметрией возможных исходов, можно применить прием, который называется непосредственным подсчетом вероятностей. Несмотря на ограниченную сферу практического применения этой схемы, она все же представляет определенный интерес, так как свойства вероятностей на этом примере отслеживаются легче всего.

1. Полная группа событий. Говорят, что несколько событий в данном опыте образуют полную группу, если в результате опыта неизбежно должно появиться хотя бы одно из них.

2. Несовместные события. Несколько событий в данном опыте называются несовместными, если никакие из них не могут появиться вместе.

3. Равновозможные события. Несколько событий в данном опыте называются равновозможными, если по условиям симметрии есть основание считать, что ни одно из них не является объективно более возможным, чем другое.

Если опыт обладает симметрией возможных исходов, то случаи представляют собой исчерпывающий набор его равновозможных и исключающих друг друга исходов. Про такой опыт говорят, что он сводится к схеме случаев. Для таких опытов возможен непосредственный подсчет вероятностей, основанный на подсчете доли так называемых благоприятных случаев в их числе.

Если опыт сводится к схеме случаев, то вероятность события А в данном опыте можно вычислить как долю благоприятных случаев в общем их числе (классическая формула):

,

где m_А – число случаев, благоприятных событию; n – общее число случаев.

Так же при решении многих задач используется формула числа сочетаний. Число сочетаний из k элементов по l – это число способов, какими можно выбрать l различных элементов из k:

.

Привести примеры множеств и их пересечений.

Условная вероятность события

Пусть производится опыт со случайным исходом в результате которого могут произойти (или не произойти) какие-то события А и В.

Условной вероятностью события В при наличии события А называется величина

,

Р(А)0.

На практике вышеупомянутую формулу читают «в обратном порядке», то есть

,

то есть вероятность произведения (пересечения, совмещения двух событий) равна вероятности одного из них, умноженной на условную вероятность второго при наличии первого. Сформулированное правило называют правилом умножения вероятностей или теоремой умножения вероятностей. Оно легко распространяется на случай произвольного числа событий:

,

то есть вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого последующего события вычисляется при условии, что все предыдущие имели место.

Для независимых событий правило умножения вероятностей принимает следующий вид:

,

то есть вероятность произведения двух независимых событий равна произведению вероятностей этих событий. Для нескольких независимых событий

.

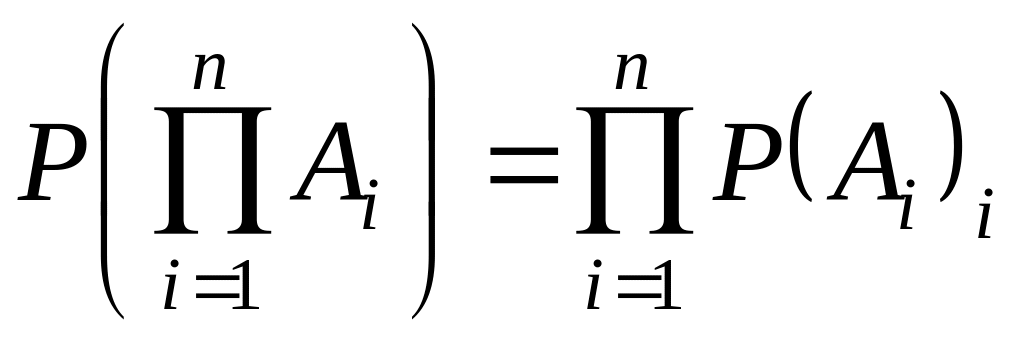Если в рассматриваемой задаче противоположное событие распадается не меньшее число вариантов, чем интересующее событие А, то имеет смысл при вычислении вероятности переходить к противоположному событию.

Примеры.

Формула полной вероятности

Следствием основных правил теории вероятностей – правила сложения и правила умножения – является формула полной вероятности.

Допустим, что предполагалось провести опыт, об условиях которого можно сделать n исключающих друг друга предположений (гипотез)

, .

Каждая гипотеза осуществляется случайным образом и представляет собой некоторое событие. Вероятности гипотез известны и равны соответственно

; ; …; .

Рассматривается некоторое событие А, которое может появиться только вместе с одной из гипотез. Заданы условные вероятности события А при каждой из гипотез:

, ; …; .

Требуется найти вероятность события А. Для этого представим А как сумму n несовместных вариантов:

.

По правилу сложения вероятностей

.

По правилу умножения

.

Откуда

,

то есть безусловная вероятность события А в опыте с гипотетическими условиями вычисляется как сумма произведений вероятности каждой гипотезы на условную вероятность события при этой гипотезе. Эта формула называется формулой полной вероятности.

Пример.

Теорема гипотез (формула Бейеса).

Следствием правила умножения и формулы полной вероятности является теорема гипотез или формула Бейеса.

Представим себе следующую ситуацию. До опыта о его условиях можно было сделать ряд гипотез, , несовместных и образующих полную группу:

, .

Вероятности гипотез до опыта (так называемые «априорные вероятности») заданы и равны

; ; …; ; .

Теперь предположим, что опыт произведен, и в результате появилось событие А. Спрашивается, как нужно пересмотреть вероятности гипотез с учетом этого факта? Другими словами, найти «апостериорные» вероятности гипотез при условии, что опыт дал результат А:

, ; …; .

Решим эту задачу, пользуясь правилом умножения и формулой полной вероятности.

Возьмем любую гипотезу H_i и вычислим вероятность произведения H_iA по правилу умножения в двух формах:

.

Теперь отбросим левую часть:

.

и разделим обе части равенства на Р(А) в предположении, что она не равна нулю; получим

.

Наконец, заменим Р(А) его выражением по формуле полной вероятности

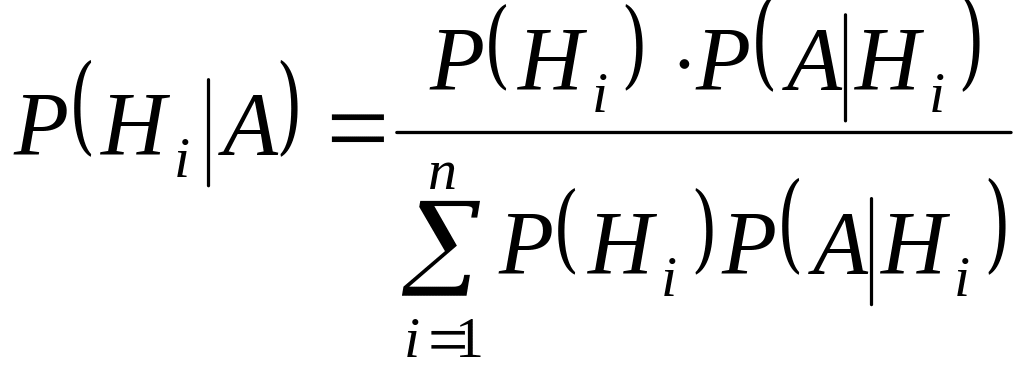, где i=1, 2, …, n.

Эта формула называется формулой Бейеса. Она позволяет пересчитывать вероятности гипотез в свете новой информации, состоящей в том, что опыт дал результат А.