1.3.3. Комплексный чертеж плоскости

Плоскость в пространстве определяют три ее точки (например A, B, C на рис. 1.21), не принадлежащие одной прямой, поэтому на комплексном чертеже всякая плоскость может быть задана проекциями этих точек (рис. 1.22). Для большей наглядности соединим точки А, В и С прямыми и получим задание плоскости треугольником АВС. При этом следует помнить, что плоскость безгранична и поэтому при решении задач некоторые построения могут выходить за пределы треугольника.

Если плоскость по мере удаления от наблюдателя поднимается вверх, то она называется восходящей. Чтобы избежать недоразумений, удаление необходимо производить по профильной прямой, принадлежащей плоскости. На комплексном чертеже проекции треугольников, которые задают восходящую плоскость, ориентированы одинаково (рис. 1.22), а для нисходящей плоскости – противоположно (рис. 1.23).

Д

Рис. 1.21	Рис. 1.22	Рис. 1.23

Рис. 1.24	Рис. 1.25	Рис. 1.26	Рис. 1.27

ля решения конкретных задач плоскость задают и другими сочетаниями образующих ее геометрических объектов: двумя пересекающимися прямыми (a∩b) (рис. 1.24), двумя параллельными прямыми (с║d) (рис. 1.25), прямой и точкой, не принадлежащей ей, (e,A) (рис. 1.26), и, наконец, следами плоскости на плоскостях проекций. Последний вариант является частным случаем задания плоскости двумя пересекающимися прямыми, а именно горизонталью и фронталю (h∩f) (рис. 1.27).

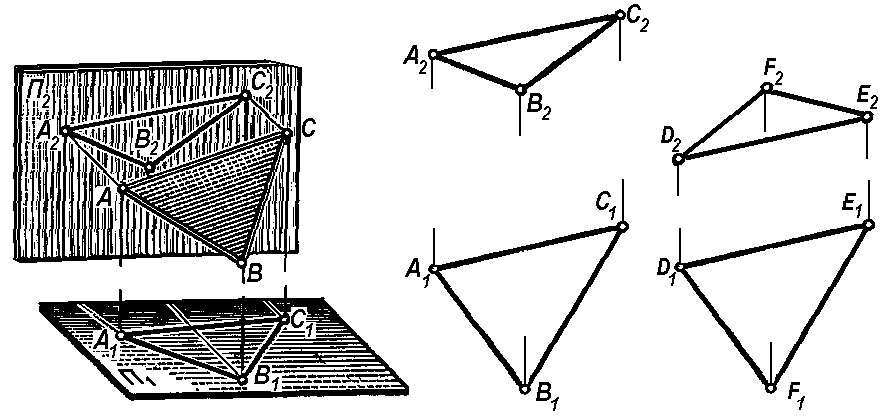
Как и для других объектов, задание на комплексном чертеже плоскости сводится к заданию совокупности независимых геометрических объектов, однозначно определяющих плоскость. Такую совокупность геометрических объектов, однозначно определяющих более сложные объекты пространства, в начертательной геометрии принято называть определителем.

Как правило, запись определителя состоит из двух частей:

• геометрической, состоящей из обозначения совокупности геометрических фигур (точек, линий);

• словесной, включающей наименование объекта и дополнительные сведения о его форме и положении в пространстве.

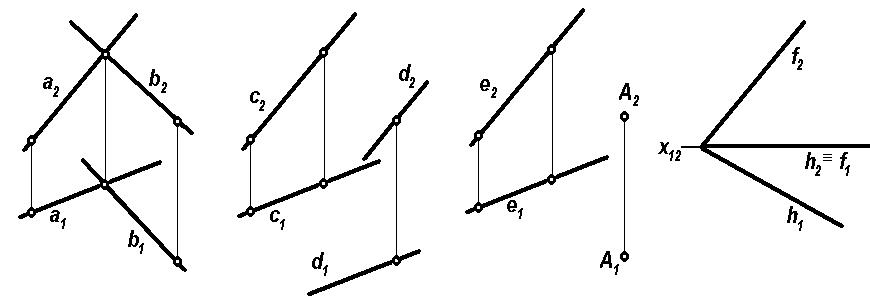
Например, определитель плоскости, комплексный чертеж которой приведен на (рис. 1.23), будет выглядеть следующим образом:

Σ(DFE) – нисходящая плоскость,

а плоскости на рис. 1.24:

Δ(a∩b) – восходящая плоскость.

Если плоскость параллельна или перпендикулярна, по крайней мере, одной из плоскостей проекций, то она называется плоскостью частного положения. Различают шесть разновидностей плоскостей частного положения.

1. П

   Рис. 1.28

   лоскость, перпендикулярная к горизонтальной плоскости проекций, называется горизонтально проецирующей. Все точки и прямые такой плоскости проецируются на горизонтальную плоскость проекций в прямую, которая и является горизонтальной проекцией горизонтально проецирующей плоскости (рис. 1.28). Фронтальная и профильная проекции ее занимают соответственно все поле проекций П₂ и П ₃.

Таким образом, горизонтально проецирующая плоскость, например Σ(а∩b) (рис.1.28), вполне определяется ее одной проекцией Σ₁. Очевидно, что α и γ – углы наклона плоскости Σ к фронтальной и профильной плоскостям проекций.

2. Плоскость, перпендикулярная к фронтальной плоскости проекций, называется фронтально проецирующей. Ее фронтальная проекция является прямой, а горизонтальная и профильная проекции занимают соответственно все поле проекций П₁ и все поле проекций П₃ (рис. 1.29). Фронтально проецирующая плоскость Τ(l,A) вполне определяется одной ее проекцией Т₂. Углы α и γ измеряют углы наклона плоскости к плоскостям проекций П₁ и П₃ соответственно. На комплексном чертеже (рис. 1.29) точка АТ.

3. П

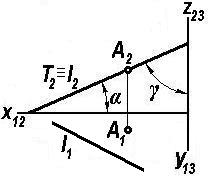
   Рис. 1.29

   лоскость, перпендикулярная к профильной плоскости проекций, называется профильно проецирующей. Ее профильная проекция является прямой, а горизонтальная и фронтальная проекции занимают соответственно все поле

п

Рис. 1.30

роекций П₁ и П ₂ (рис. 1.30). Профильно проецирующая плоскость Γ(m║n) вполне определяется одной ее проекцией Γ₃. Углы α и β измеряют углы наклона плоскости Γ к плоскостям проекций П₁ и П ₂ соответственно.

Плоскости, параллельные одной из плоскостей проекций, называют плоскостями уровня, т. к. все точки, принадлежащие им, одинаково удалены от соответствующих плоскостей проекций.

4. Плоскость Δ(АВС) (рис. 1.31), параллельную горизонтальной плоскости проекций, называют горизонтальной плоскостью уровня.

5. Плоскость Θ(DEF) (рис. 1.32), параллельную фронтальной плоскости проекций, называют фронтальной плоскостью уровня.

6. П

   Рис. 1.31	Рис. 1.32	Рис. 1.33

   лоскость Λ(GHI) (рис. 1.33), параллельную профильной плоскости проекций, называют профильной плоскостью уровня.

Каждая плоскость уровня является в то же время проецирующей плоскостью. Фигуры, принадлежащие горизонтальной плоскости уровня Δ, фронтальной плоскости – Θ, профильной плоскости – Λ, проецируются без искажений соответственно на плоскости проекций П₁, П ₂, П ₃ (рис. 1.31, 1.32, 1.33).