1.3. Комплексный чертеж линейных геометрических объектов

1.3.1. Комплексный чертеж точки

П

Рис. 1.12	Рис. 1.13

оложение проекций точек на поле проекций комплексного чертежа зависит от того, в какой четверти и на каком расстоянии от плоскостей проекций находится данная точка. Так, если точка А расположена во второй четверти (рис 1.12), то после совмещения плоскостей проекций на комплексном чертеже обе проекции точки окажутся лежащими над осью проекций х₁₂ (рис. 1.13).

Если точка В находится в третьей четверти, то ее горизонтальная проекция на комплексном чертеже окажется над осью проекций, а фронтальная – под осью. Наконец, если точка С расположена в четвертой четверти, то обе проекции ее окажутся под осью х₁₂.

Встречаются случаи, когда точки занимают некоторые частные (особые) положения, а именно принадлежат плоскостям проекций. При этом, если точка принадлежит только одной плоскости проекций, то на комплексном чертеже одна из проекций совпадает с самой точкой, а другая проекция точки принадлежит оси проекций. Это хорошо видно на примере точки D (рис. 1.12 и 1.13). Если же точка принадлежит обеим плоскостям проекций (точка Е), то на комплексном чертеже обе проекции совмещаются с самой точкой и принадлежат оси х₁₂.

Большой практический интерес представляют случаи взаимного положения двух точек, когда их одноименные проекции на комплексном чертеже совпадают. Так точки F и K на рис. 1.12 расположены на одном перпендикуляре (луче проекций) к горизонтальной плоскости проекций, и поэтому их горизонтальные проекции совпадают (рис. 1.13). Такие точки называются горизонтально конкурирующими. Точка F выше точки К, т. е. F ближе к наблюдателю, а следовательно, на комплексном чертеже горизонтальная проекция точки F₁ будет видна, а К₁ – невидна. На комплексных чертежах невидимые точки принято заключать в круглые скобки.

Точки М и N рисунке 1.12 расположены на одном перпендикуляре к фронтальной плоскости проекций, поэтому фронтальные проекции этих точек совпадают (рис. 1.13). Такие точки называют фронтально конкурирующими. Точки М находится ближе к наблюдателю, чем точка N, а следовательно, фронтальная проекция последней N₂ будет невидна.

1.3.2. Комплексный чертеж прямой

Положение прямой в пространстве вполне может быть задано двумя точками, принадлежащими этой прямой. Таким образом, чтобы получить комплексный чертеж некоторой прямой l (рис. 1.14), достаточно построить проекции двух произвольных точек А(А₁,А₂) и В(В₁,В₂) (рис. 1.15), которые принадлежат прямой l и полностью определяют положение ее в пространстве.

Э

Рис. 1.14	Рис. 1.15	Рис. 1.16

ти две произвольные точки А и В представляют минимальное число постоянных и независимых геометрических элементов, определяющих прямую l. В этом случае для обозначения прямой используется запись – l(A,B), которую называют определителем объекта.

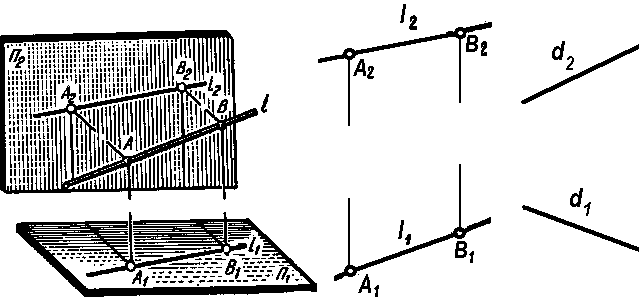
Кроме того, прямую задают проекциями отрезка d(d₁,d₂) (рис. 1.16), без предварительного выбора конкретных точек, принадлежащих этой прямой.

Прямые, не параллельные и не перпендикулярные ни одной из плоскостей проекций, называются прямыми общего положения. Прямые общего положения бывают восходящими и нисходящими.

У прямой l на рис. 1.14 ближайшая к наблюдателю точка А (наблюдатель предполагается стоящим лицом к плоскости П₂) расположена ниже, чем более удаленная от наблюдателя точка В. Следовательно, прямая l по мере удаления от наблюдателя поднимается вверх, поэтому такую прямую называют восходящей и для ее идентификации используется определитель:

l(A,B) – восходящая прямая.

Если же прямая по мере удаления от наблюдателя понижается, то такую прямую называют нисходящей. Например, d(d₁,d₂) – нисходящая прямая, комплексный чертеж которой приведен на рисунке 1.16.

Н

Рис. 1.17

а комплексном чертеже проекции восходящей прямой наклонены к линиям проекционных связей в одну и ту же сторону (рис. 1.15), а проекции нисходящей прямой наклонены в разные стороны к линям проекционных связей.

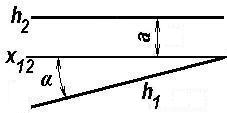
Прямые, параллельные или перпендикулярные плоскостям проекций, называют прямыми частного положения.

П

Рис. 1.18

рямые, которые параллельны одной из плоскостей проекций, называют прямыми уровня (рис. 1.17, 1.18, 1.19).

Фронтальная проекция прямой h параллельна оси проекций х₁₂ (рис. 1.17), следовательно, высоты а всех точек этой прямой равны между собой, поэтому h параллельна горизонтальной плоскости проекции П₁. Такая прямая называется горизонтальной прямой или горизонталью.

Отрезок горизонтали проецируется на плоскость П₁ без искажений, как говорят, в натуральную величину. На комплексном чертеже рис.1.17 α – угол наклона прямой h к фронтальной плоскости проекций.

Горизонтальная проекция прямой f параллельна оси проекций х₁₂ (рис. 1.18), следовательно, глубины b всех точек этой прямой равны между собой, поэтому f параллельна фронтальной плоскости проекции П₂. Такая прямая называется фронтальной прямой или фронталью.

О

Рис. 1.19

трезок фронтали проецируется на П₂ в натуральную величину, а угол наклона f к плоскости П₁ равен β.

Прямая p, три проекции которой приведены на рисунке 1.19, параллельна профильной плоскости проекции П₃. Подобные прямые называются профильными прямыми.

Следует иметь в виду, что для однозначного определения положения в пространстве профильных прямых необходимо на двухкартинном комплексном чертеже задавать не только их проекции, но и проекции принадлежащих им точек (например, А,В и C,D рис. 1.19).

П

Рис. 1.20

рямые, перпендикулярные к одной из плоскостей проекций, называют проецирующими прямыми (рис. 1.20).

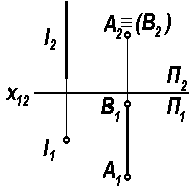
Если прямая, например l, перпендикулярна горизонтальной плоскости проекций П₁, то на эту плоскость она спроецируется в точку l₁. Подобные прямые называют горизонтально проецирующими.

Если прямая, например АВ, перпендикулярна фронтальной плоскости проекций П₂, то на этой плоскости фронтально конкурирующие точки А и В спроецируются в одну точку. Подобные прямые называют фронтально проецирующими.