1.8. Способы преобразования комплексного чертежа

В начертательной геометрии используется графический способ решения практических задач. Количество и характер графических построений при этом определяются не только сложностью задачи, но и в значительной мере зависят от того, с какими проекциями (удобными или неудобными) приходится иметь дело. Задачи решаются значительно проще в случае частного положения геометрических объектов относитель­но плоскостей проекций. Для этого прибегают к преобразованиям комплексного чертежа.

С помощью преобразований решаются четыре основные для начертательной геометрии задачи:

• прямую общего положения преобразуют в прямую уровня;

• прямую общего положения преобразуют в проецирующую прямую.

• плоскость общего положения преобразуют в проецирующую плоскость;

• плоскость общего положения преобразуют в плоскость уровня.

На практике для решения этих задач применяют способы, которые можно разделить на три группы:

• замена плоскостей проекций;

• плоскопараллельное перемещение объекта;

• использование дополнительного проецирования.

Заменяя плоскости проекций, добиваются желаемого результата изменением положения в пространстве плоскостей проекций, при этом объект остается неподвижным.

При плоскопараллельном перемещении плоскости проекций остаются неподвижными, тогда как объект перемещается в пространстве по определенному закону.

При использовании способов дополнительного проецирования ни объект, ни плоскости проекций не меняют своего положения в пространстве, а нужное решение получают за счет изменения направления проецирования.

1.8.1. Способ замены плоскостей проекций

Способ замены плоскостей проекций состоит в том, что одна из основных плоскостей проекций (П₁, П₂ или П₃) заменяется новой плоскостью проекций П₄, расположенной относительно объекта рациональным образом в зависимости от решаемой задачи (рис. 1.79). К этой плоскости проекций предъявляется единственное требование – она должна быть перпендикулярной к незаменяемой плоскости проекций.

Так, если заменяется плоскость проекций П₂, то новая плоскость П₄ должна быть перпендикулярна к незаменяемой плоскости П₁ (рис. 1.79), если же заменяется плоскость проекций П₁, то плоскость П₄ должна быть перпендикулярна к плоскости П₂.

В

Рис. 1.79

результате замены одной из основных плоскостей проекций на плоскость П₄ получается вместо старой системы плоскостей проекций (П₁,П₂) новый комплексный чертеж, образованный плоскостями проекций П₁ и П₄. При этом положение новой плоскости проекций П₄ фиксируется осью проекций x₁₄.

В полученной системе плоскостей проекций можно произвести замену оставшейся незамененной плоскости П₁ на новую плоскость П₅, перпендикулярную незаменяемой плоскости П₄. Последовательное введение новых плоскостей проекций П₄, П₅, П₆, … позволяет получить такую систему плоскостей проекций, в которой изучаемый объект займет удобное для решения конкретной задачи положение.

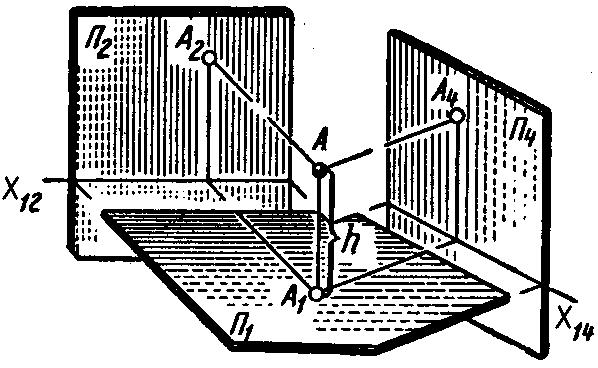
Рассмотрим ход выполнения на комплексном чертеже замены плоскостей проекций.

Точка А задана своими проекциями А₁ и A₂ в системе плоскостей проекций (П₁,П₂). Заменим плоскость П₂ на новую плоскость П₄, перпендикулярную к плоскости П₁. После этого, спроецируем точку А на эту новую плос­кость проекций, обозначив полученную проекцию через A₄ (рис. 1.80).

Т

Рис. 1.80

ак как горизонтальная проекция А₁ точки А остается неизменной, то через эту проекцию в направлении, перпендикулярном оси проекций x₁₄, проводим новую линию проекционных связей А₁А₄. Поскольку точка А и плоскость проекций П₁ не меняли своего положения при данном преобразовании, то расстояние от точки А до плоскости П₁ осталось неизменным. Это расстояние h, измеренное в системе плоскостей проекций (П₁,П₂), необходимо отложить от оси проекций x₁₄ по новой линии проекционных связей А₁А₄ (рис. 1.80). В результате этих действий, получаем новую проекцию A₄ точки А.

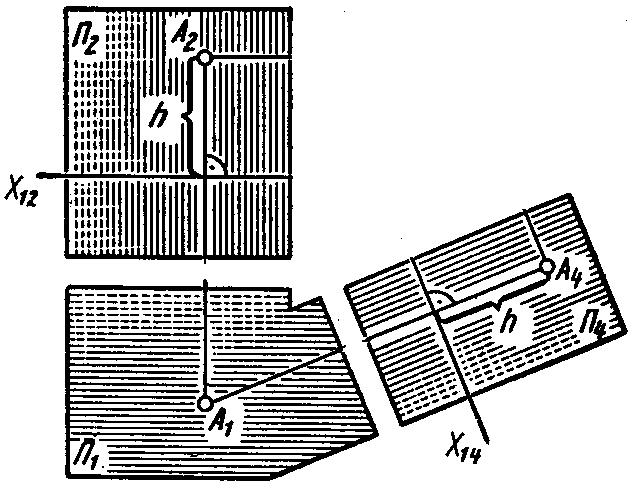
Таким образом, для построения на комплексном чертеже новой проекции точки при замене любой из плоскостей проекций необходимо:

• провести через незаменяемую проекцию точки новую линию проекционных связей (в направлении, отвечающем требованиям решаемой задачи);

• в направлении, перпендикулярном новой линии проекционных связей, провести новую ось проекций;

• измерить расстояние от заменяемой проекции точки до заменяемой оси проекций и отложить это расстояние на новой линии проекционных связей от новой оси проекций.

Р

Рис. 1.81

ассмотрим четыре основные задачи, к которым сводится решение различных задач способом замены плоскостей проекций.

1.8.1.1. Прямую l общего положения преобразовать в прямую уровня (рис. 1.81).

Отличие этой задачи от рассмотренного выше примера заключается в том, что там выбор плоскости проекций П₄ обуславливался тем, чтобы она была перпендикулярна плоскости П₁. В данной задаче плоскость П₄, кроме этого требования, должна быть параллельна горизонтальной проекции l₁ прямой l, что на комплексном чертеже может быть выполнено, если ось проекций x₁₄ будет проведена параллельно l₁.

В результате решения этой задачи прямая l проецируется на плоскость проекций П₄ без искажения, а угол α, образованный проекцией l₄ с ось проекций x₁₄, дает натуральный угол наклона прямой l к плоскости проекций П₁.

1.8.1.2. Прямую l общего положения преобразовать в проецирующую прямую (рис. 1.82).

Для решения этой задачи необходимо последовательно провести две зам

Рис. 1.82

ены:

• с помощью первой замены плоскостей проекций (П₁,П₄) прямая l преобразуется в линию уровня;

• вторая замена плоскостей проекций (П₄,П₅) позволяет преобразовать прямую l в проецирующую.

1.8.1.3. Плоскость общего положения Θ(А,В,С) преобразовать в проецирующую плоскость (рис. 1.83).

Е

Рис. 1.83

сли провести принадлежащую данной плоскости линию уровня, например горизонталь h, то, заменяя плоскость проекций П₂ на плоскость П_4, перпендикулярную к этой горизонтали, а значит, перпендикулярную и к незаменяемой плоскости проекций П₁, получим горизонталь и данную плоскость Θ(А,В,С) проецирующими относительно плоскости П₄.

Угол α, образованный проекцией Θ₄ с осью проекций x₁₄, дает натуральный угол наклона плоскости Θ к плоскости проекций П₁.

1.8.1.4. Плоскость общего положения Θ(А,В,С) преобразовать в плоскость уровня (рис. 1.84).

Для решения этой задачи, так же как и для второй, необходимо последовательно провести две замены:

• с помощью первой замены плоскостей проекций (П₁,П₄) плоскость Θ(А,В,С) преобразуется в проецирующую;

• вторая замена плоскостей проекций (П₄,П₅) превращает данную плоскость в плоскость уровня, т. е. в плоскость, параллельную к плоскости проекций П₅, поэтому проекция А₅В₅С₅ треугольника АВС дает натуральный вид этого треугольника

Р

Рис. 1.84

ассмотрим пример задачи, в которой используется один из способов замены плоскостей проекций: из точки А опустить перпендикуляр на прямую l общего положения.

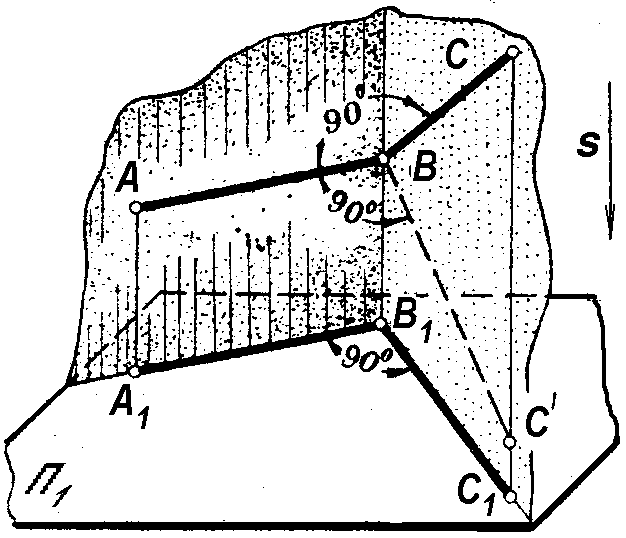
Прежде чем приступить к решению этой задачи, познакомимся еще с одним свойством линейного параллельного ортогонального проецирования: прямой угол, образованный отрезками прямых, проецируется без искажения (прямым углом), если одна из его сторон параллельна плоскости проекций (рис. 1.85).

Е

Рис. 1.85

сли сделать заданную прямую l прямой уровня, заменяя плоскость П₂ на плоскость П₄║l (смотри первую основную задачу), то можно провести искомый перпендикуляр, т. к. перпендикулярность к прямой уровня сохранится при этой замене на плоскости проекций П₄ (рис. 1.86). Поэтому, опустив из новой проекции А₄ точки А перпендикуляр на новую проекцию l₄ прямой l, получим проекцию А₄В₄ искомого перпендикуляра. Возвращаясь в основную систему плоскостей проекций (П₁,П₂), получаем проекции А₁В₁ и А₂В₂ искомого перпендикуляра.