1 Рис. 1.60 .5.4.3. Различают три разновидности линейчатых поверхностей с одной направляющей:

• коническая поверхность общего вида образуется движением прямолинейной образующей l по некоторой кривой линии m (направляющей) и имеющей неподвижную точку S (вершину) (рис. 1.60). Определитель поверхности имеет вид:

Ф(m,S) – коническая поверхность;

• цилиндрическая поверхность образуется в результате движения прямолинейной образующей l по некоторой кривой линии m (направляющей) и имеющей постоянное направление s (рис. 1.61). Определитель поверхности имеет вид:

Ф (m,s) – цилиндрическая поверхность.

Если направляющей является ломаная линия, то получаются частные случаи конической и цилиндрической поверхностей – пирамидальная и призматическая поверхности;

• торс образуется движением прямолинейной образующей l, касающейся во всех своих положениях некоторой пространственной кривой m, называемой ребром возврата. Ребро возврата является направляющей торса, который полностью определяет поверхность (рис. 1.62). В связи с этим определитель поверхности содержит только один элемент:

Ф(m) – торс.

Коническую и цилиндрическую поверхности можно рассматривать как частные случаи поверхности торса, когда ее ребро возврата вырождается в точку (конечную или бесконечно удаленную).

Линейчатые поверхности с одной направляющей относятся к числу развертывающихся поверхностей. Все другие линейчатые кривые поверхности относятся к числу неразвертывающихся, их так же называют косыми.

1.5.5. Поверхности второго порядка

Поверхностью второго порядка называется геометрический образ, определяемый уравнением второй степени в пространственной системе координат, т. е. такая поверхность, которая несет на себе семейство кривых второго порядка. К поверхностям второго порядка относятся различные виды цилиндрических и конических поверхностей, эллипсоидов, параболоидов и гиперболоидов.

На комплексных чертежах поверхности второго порядка задаются проекциями их главных меридианов, т. е. геометрическая часть определителя поверхности содержит элементы, которыми являются кривые второго порядка. Например, эллиптический параболоид, комплексный чертеж которого приведен на рис. 1.63, описывается следующим определителем:

Ф

Рис. 1.63

(a,b) – эллиптический параболоид,

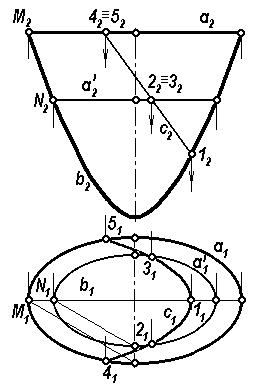
где a – эллипс, b – парабола.

На комплексном чертеже эллиптического гиперболоида Ф (рис. 1.63) построена с использованием элементов его каркаса линия .

1.5.6. Циклические поверхности

Циклическими называются поверхности, которые образованы движением окружности переменного радиуса по определенному закону. Из определения следует, что на всякой циклической поверхности располагается семейство окружностей различного радиуса.

Второе семейство линий (направляющих) может состоять из различных кривых в зависимости от закона движения образующих, который задается аналитически или графически.

Ч

Рис. 1.64

астным видом циклических поверхностей являются каналовые поверхности, которые образуются движением окружности переменного радиуса так, что центр окружности перемещается по заданной кривой (линии центров), а плоскость окружности остается перпендикулярной к этой кривой (рис. 1.64). Определитель такой поверхности имеет вид:

Ф(i, b) – каналовая поверхность,

где i – линия, которая задает закон движения центров образующих окружностей, а b – характеризует закон изменения радиусов этих окружностей.

Горизонтальные проекции образующих k и k^I каналовой поверхности являются эллипсами, построение которых на комплексном чертеже показано на рис. 1.64 по двум их (большей и меньшей) осям. Горизонтальный очерк каналовой поверхности строится в виде касательной к линиям ее образующих.

Если образующие окружности каналовой поверхности имеют постоянный радиус при движении по заданному закону, то такая поверхность называется трубчатой.