1.5.4. Линейчатые поверхности

Линейчатой называют поверхность, которая образуется движением прямой линии (образующей) в пространстве. В зависимости от закона движения образующей прямой выделяют три вида линейчатых поверхностей.

1

Рис. 1.55

.5.4.1. Линейчатые поверхности с тремя направляющими образуются движением прямолинейной образующей по трем направляющим a, b и c (кривым или прямым), которые единственным образом определяют движение образующей l (рис. 1.55). Так, выбрав на направляющей a любую точку А, можно будет провести через эту точку бесконечное множество прямолинейных образующих конической поверхности с вершиной в точке А и пересекающих направляющую c. Из рис. 1.55 видно, что через точку А, взятую на направляющей a, проходит одна и только одна прямолинейная образующая, пересекающая две другие направляющие b и c.

О

Рис. 1.56

писанным способом через точки, принадлежащие направляющей a, можно построить любое число прямолинейных образующих, которые выделят в пространстве одну единственную линейчатую поверхность.

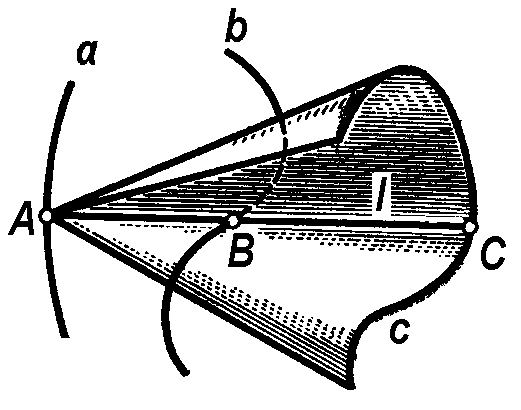
Так как положение прямолинейных образующих однозначно определяется формой и положением в пространстве направляющих a, b и c, то определитель линейчатой поверхности рассматриваемого вида записывается как:

Ф(a,b,c) – линейчатая поверхность.

Примером линейчатой поверхности с тремя направляющими является однополосный гиперболоид, у которого направляющими служат три произвольно скрещивающиеся прямые a, b и c (рис. 1.56).

Часто линейчатые поверхности задаются меньшим числом направляющих. В этих случаях отсутствие недостающих направляющих дополняют условиями, обеспечивающими заданный характер движения образующей.

1

Рис. 1.57

.5.4.2. Для получения линейчатых поверхностей с двумя направляющими задается дополнительное условие сохранения параллельности образующей какой-либо плоскости, называемой плоскостью параллелизма, или сохранения заданного угла наклона образующей относительно какой-либо плоскости или оси вращения (у геликоидов). Такие поверхности называются поверхностями с плоскостью параллелизма. К ним относятся:

• цилиндроид образуется движением прямолинейной образующей l по двум криволинейным направляющим a и b, причем во всех своих положениях образующая параллельна некоторой плоскости параллелизма Σ (рис. 1.57). Определитель поверхности имеет вид:

– цилиндроид.

На комплексном чертеже (рис. 1.5)7 с использованием каркаса поверхности построена точка А, которая принадлежит цилиндроиду. Точка А построена по принципу принадлежности линии с, которая в свою очередь принадлежит поверхности цилиндроида Ф:

.

Обычно для удобства построения образующих линейчатых поверхностей за плоскость параллелизма принимают одну из плоскостей проекций, тогда образующие будут соответствующими линиями уровня;

• коноид образуется движением прямолинейной образующей l по двум направляющим, из которых одна является кривой линией a, а другая – прямой b, причем во всех своих положениях образующая параллельна некоторой плоскости параллелизма Σ. Определитель поверхности имеет вид:

– коноид.

Если у коноида прямолинейная направляющая b перпендикулярна плоскости параллелизма, то коноид называется прямым. На рис. 1.58 показан прямой коноид с плоскость параллелизма П₁, у которого образующие являются горизонталями;

• косая плоскость образуется движением прямолинейной образующей l по двум скрещивающимся прямолинейным направляющим a и b, причем во всех своих положениях образующая параллельна некоторой плоскости параллелизма Σ. Определитель поверхности имеет вид:

– косая плоскость.

Если направляющие a и b будут не скрещивающиеся прямые, а пересекающиеся или параллельные, то косая плоскость выродится в обыкновенную плоскость, которой принадлежат направляющие a и b.

Н

Рис. 1.58	Рис. 1.59

а рис. 1.59 изображена косая плоскость, направляющими которой служат прямые a и b, а плоскость параллелизма – горизонтальная плоскость проекций П₁, следовательно, образующие косой плоскости являются горизонталями.

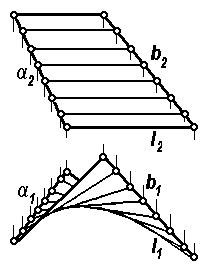
Так как в сечении косой плоскости можно получить, кроме прямолинейных образующих и направляющих, также гиперболу и параболу, эту поверхность еще называют гиперболическим параболоидом. Параболой является горизонтальный очерк косой плоскости, приведенной на рис. 1.59.