Выбор примитивов
Выбор примитивов должен быть таким, чтобы, в первую очередь, они отображаю значение подавляющего большинства направлений аппроксимирующих отрезков
прямой .
На рис-6,а приведенная|наведенная| гистограмма для аппроксимации ЭКГ отрезками прямой ва| интервалах единичной длины (рис.6,б). Чтобы можно было нормировать отрезки длины аппроксимирующих линий, нужно отобразить сигнал в плоскости, в которой|какой| координаты имеют то же физическое значение; этого можно достичь, например, для ЭКГ следующими нормирующими отношениями: Y = 10 IU (мм; мВ|) и X = 25 t (м; с). Из|с| гистограммы на рис.1.9,а выходит, что в сигнале с пять доминантных направлений:
<ВН> большой|великий| негативный наклон|наклонение,предрасположение| (в диапазоне -90° ... -70°);
<Н> негативный наклон|наклонение,предрасположение| (в диапазоне -70° ... -15°);
<Г> горизонтальные сегменты (в диапазоне -15° ... +10°);
<П> позитивный|положительный| наклон|наклонение,предрасположение| (в диапазоне +10° ... +70°);
<ВП> большой|великий| позитивный|положительный| наклон|наклонение,предрасположение| (в диапазоне +70° ... +90°).
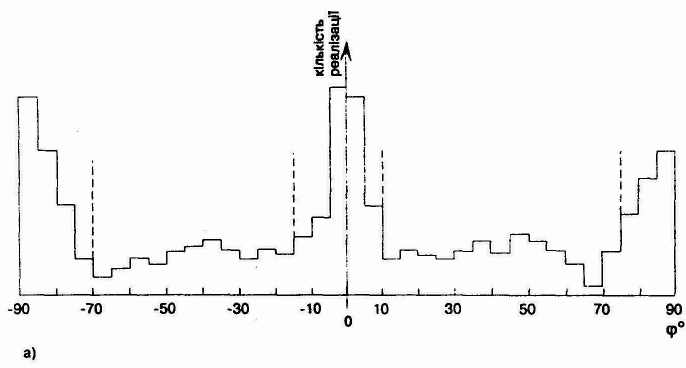
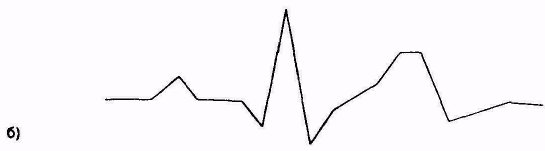
Рисунок| 6-гистограмма для аппроксимации ЭКГ
Эти символы для описания ЭКГ можно считать примитивами. Эти примитивы можно дальше дополнить дополнительными атрібутами| (время существования примитива, координаты начала и конца, и тому подобное).
Эвристическое описание
Сигнал ЭКГ состоит из последовательности элементов, которые|какие| отображают базовые фазы электрической активности сердечной мышцы (рис.7) - волна P, интервал PQ, комплекс QRS; сегмент ST; волна Т; интервал ТР| и тому подобное. Эти элементы можно считать базовыми элементами описания сигнала и сигнал описать цепью соответствующих символов, которые|какие| опять|снова| могут быть дополнены атрибутами, которые|какие| ближе специфицируют конкретный сигнал в рамках одиночных примитивов (уровень сигнала, экстремумы сигнала, длительность, морфология и тому подобное). Распознавание таким образом выбранных|избранных| примитивов не является тривиальной задачей, для этого используют разные|различные| алгоритмы из|с| области распознавания признаков.
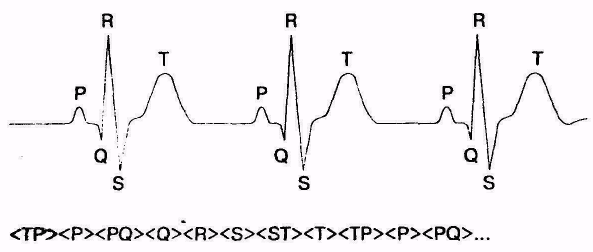
Рисунок| 7- Базовые фазы электрической активности сердечной мышцы
Кумулятивные методы обработки сигналов
Кумулятивные методы предназначенны для увеличения отношения сигнал/шум в случаях, когда полезный сигнал имеет репетиционный характер, в то время, как шум считают стационарным с нулевым средним.
В практике сравнительно часто возникают случаи приема репетиционного сягнала|, уровень которого|какого| может оказаться сравнительным, или существенно ниже, чем среднее квадратичное отклонение шума|, что с ним складывается|состоит|.
Под репетиционным сигналом понимают сигнал ограниченной длины, который|какой| после определенного (обычно не постоянного|устоявшегося|) интервала опять|снова| повторяется.
Удобно, когда появление сигнала| стимулируется наблюдателем, как это имеет место, например, для евокованих| (вызванных) потенциалов в ЕЕГ|, что отвечают отзыву нервной системы на оптическое или акустическое возбуждение. Кумулятивные алгоритмы также легко использовать в случае, когда полезный сигнал повторяется во времени периодически.
В случае "почти периодических|периодичных|" сигналов (это, например, електро-кардограми| плода в теле матери) малые часовые посуви| между кумульованими| сигналами могут привести к|до| значительным искажениям|обезображиваниям|. Сложным становится|стает| использование|употребление| кумулятивных алгоритмов, если нет априорной информации про| начало каждой репетиции и его нужно определить перед каждой кумуляцией. Сложность есть в том, что отдельная репетиция полезного сигнала замаскирована шумом, потому|оттого| вычисление|исчисление| ее начала часто нуждается в громоздких процедурах.
Базовая идея кумулятивных алгоритмов чрезвычайно простая (рис.8). Из входного сигнала| выбирают сегменты с репетициями полезного сигнала|.
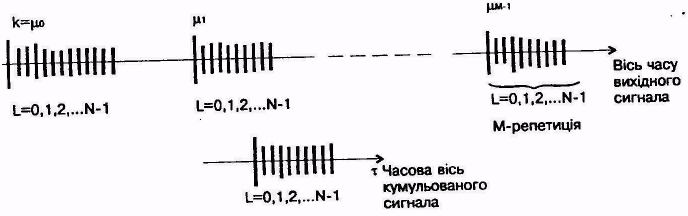
Рисунок| 8- Кумулятивный алгоритм
Разместим на вспомогательной осе времени И репетиции так, чтобы моменты их начала совпадали. Тогда их мгновенные значения (возможно, умноженные|помноженные| на соответствующие взвешивающие коэффициенты) будем добавлять|прибавлять,додавать| в одно и то же мгновение|миг|
времени.
Ясно, что полезная составляющая сигнала| задана в этом случае суммой
одинаковых репетиций.
При этом шум, поскольку он имеет случайный характер с нулевым средним (как этого можно интуитивно ожидать), будет иметь тенденцию к|до| уменьшению (в случае выполнения определенных требований), поскольку в одни и те же моменты сумуються| значения с разными|различными| (в среднем) знаками.
Если взвешивающие коэффициенты выбраны|избраны| корректно, значение выходного сигнала| является средним или взвешенным средним избранного количества реализаций
(репетиций).
Потому|оттого| кумулятивные алгоритмы иногда называют алгоритмами усреднения, что является переводом английского ауега§іпЈ. Но этот срок|термин| не достаточно однозначен.
В результате кумуляции всегда присутствующий "остаток|остача|" шума, который|какой| нужно было бы|б| дальше подавить.
Кумулятивные алгоритмы
Рассмотрим кумулятивную обработку дискретных сигналов, причем будем считать, что моменты начала репетиций полезного сигнала отвечают моментам| дискретного времени.
Входной сигнал х(mТ) (m-й дискрег|) образован адитивною| смесью полезного сигнала| и шума| на сегменте і-ї| репетиции, имеет вид
x(mТ)= s(mТ)+ п(mТ) (1.13)
где s(mТ)= s[(m +
и)];
s(mТ) — полезный орущий сигнал конечной|концевой| длины МТ;
n(mТ) -шум;
іТ-| момент начала і-ї| репетиции;
Т - период дискретизации.
Исходный|выходной| сигнал в(mТ) (m-й дискрет|) после кумуляции на j-й репетиции описывается выражением
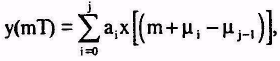(1.14)
где аi - взвешивающие коэффициенты отдельных сегментов.
Выражение (1.14) значит|означает| суперпозицию сегментов, причем влияние отдельных сегментов может быть разным|различным|. Выбором количества сегментов, которые добавляются|прибавляются,додаются|, М, и коэффициентов аi (и = 0,1..., М-1) определенный тип кумулятивного алгоритма| и его свойства. Заметим, что в зависимости от выбранных|избранных| коэффициентов а, выражение (1.14) может сходиться и тогда|и затем|, когда количество реализаций в кумуляции излишне|чрезмерно| растет|вырастает| (это используют в случае экспоненциальной кумуляции).
Выражение (1.14) отображает значение дискрета| исходного|выходного| сигнала в реальном времени и складывается|состоит| с М репетиций этого дискрета|, причем более старые (более давние) репетиции в результате могут и не учитываться.
В частном случае периодических|периодичных| репетиций (если репетиционный период LT) выражение (1.14) (для одного дискрета| кумуляции для j > L-1) можно превратить к|до| виду
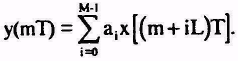(1.15)
Импульсная характеристика h(іL) устройства, что реализует (1.15), имеет вид h(-іL)= aі, (и = 0,1. ...М-1), то есть
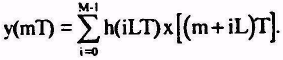(1.16)
Реализации кумулятивных алгоритмов в практике (программные аоо| в виде простых устройств) базируются на общей структурной схеме, которая|какая| приведена|наведена| на рис.1.12.
За схемой рис.1.12 соответствующие (в разных|различных| репетициях) часовые|временные| интервалы обрабатывают в независимых параллельных каналах.
Каждый из|с| кумульованих| сегментов описывают N дискретами| х[(m + и)Т], где (m + и) = L = 0,1...,N-1. В течение каждой репетиции оба переключателя пройдут все состояния|станы| таким образом, чтобы L-й канал был підімкнений| к|до| входу и выходу в момент mТ = (L + I)t
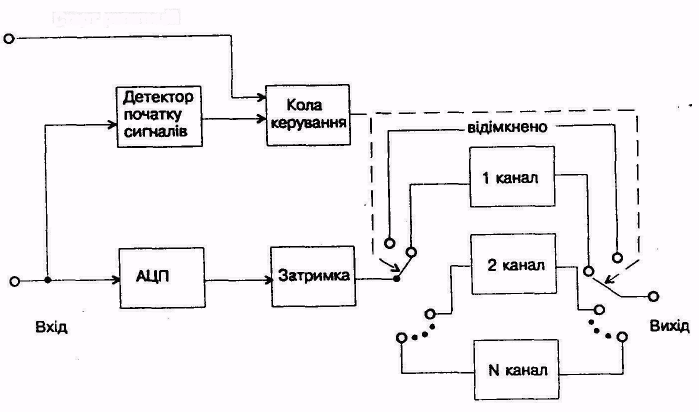
Рисунок| 8- Общая структурная схема для реализации кумулятивных алгоритмов в практике
В часовых|временных| интервалах между репетициями (N-м значением данной репетиции, что обрабатывается, и первым - следующей) все переключатели находятся в положении, при котором|каком| вход отомкнутый от выхода.
На практике используют два вида кумуляции: с постоянными|устоявшимися| весовыми коэффициентами | и с весовыми коэффициентами | |, которые|какие| уменьшаются за экспоненциальным законом.
Кумуляция с одинаковыми вагами|
В этом методе результат складывается|состоит| с М последних повторений сигнала| с приблизительно|примерно| постоянными|устоявшимися| вагами| аi = 1/М (и = 0,1,...,М-1).
Оценим, какого улучшения отношения сигнал/шум можно достичь за данным методом. Пусть шум n(t) - стационарный, а ергодичний| процесс - с нулевым математическим ожиданием, который|какой| описан однови-мерной густотой|плотностью| вероятностей р(n). Пусть также для сигнала| в течение кумуляции все репетиции идентичные. В соответствии к|до| (1.13) и (1.14) при j М-1 кумуляция одного дискрета|
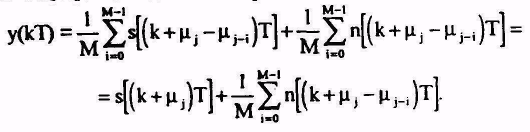(1.17)
Оценим теперь, какая дисперсия
S2
отвечает случайной величине, которая|какая|
образована суммой и является вторым
членом выражения (1.17). (Она характеризует
дисперсию шума|
после кумуляции). Можно получить выражение
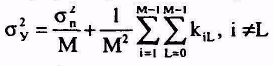(1.18)
где - kiL ковариация пар членов суммы.
Ясно, что корреляция между одноименными мгновенными значениями в разных|различных| сегментах увеличивает дисперсию шума и ухудшает возможности кумуляции. В обычном в практике случае, когда эти связи малые, двойной суммой в (1.18) можно пренебречь, и дисперсия шума| после кумуляции в М раз меньше, чем исходного|выходного| шума. Поскольку мощность полезного детермінованого| сигнала после кумуляции такая же, как и к|до| ней, отношение сигнал/шум увеличится в среднем (по напряжению или току) у М1/2 раз.
Гипотезу, что реализации шума в отдельных репетициях некоррелируемые, можно быть легкопроверяемым, если вычислить|исчисляющий| (измерять|вымерять,вымеривать|) автокорреляционную функцию шума без сигнала. Если ее значение на интервалах, которые|какие| отвечают времени репетиций (среднему) зникомо| малые, то гипотеза верна. Оттуда (в обратном порядке) можно установить минимальный интервал между репетициями (если его при измерениях можно выбирать, что в медицинских задачах не всегда удается|прибегает|). Например, в кардиограмме можно пропустить непарные|нечетные| репетиции и кумулювати| парные|четные|. Но, поскольку эти репетиции также изменяются со временем, то здесь|тут| нужно выбирать умный компромисс.
Если автокорреляционные функции имеют периодические|периодичные| составляющие (то есть и шум также), ситуация осложняется|усложняется|. Если репетиции стимулируются (вызываются внешними возбуждениями), нежелательные связи можно исключить|выключить| выбором случайных интервалов между стимулами.
Очень важно подчеркнуть, что полученный результат кумуляции верный лишь|только| в среднем, когда обрабатывают большое|великое| количество репетиций, то есть, когда реализуются законы больших|великих| чисел.
В случае кумуляции малого количества репетиций шум может и не быть (после кумуляции) заметно более малым.
Тот факт, что результаты верные лишь|только| в среднестатистическом смысле, часто в медицинской практике не принимают во внимание, а это иногда приводит к|до| неверным результатам.
На практике, также часто (с целью получения удовлетворительных результатов кумуляции) требуют, чтобы шум имел нормальное распределение или равномерный спектр, и тому подобное. Ясно, что такие требования убыточны, и единственное|единое| требование - это чтобы процесс был центрируемым|центруемым|, а реализации шума, соответствующие к|до| разным|различным| репетициям, были иекорельованими|.
Не масс значения также форма коваріаційної| функции шума| на интервале одной репетиции, то есть связи между близкими дискретами| шуму.
Кумуляция с экспоненциальными вагами|
В соответствии к|до| (1.14) индексом и = 0 обозначим|пометим| последнюю репетицию, то есть пусть теперь индекс увеличивается по направлению к прошлому. Тогда взвешивающие коэффициенты при экспоненциальной кумуляции можно определить следующим образом
(1.19)
где с > 0, потому|оттого| 0 < q < 1.
В сумме (1.14) последняя репетиция тогда учитывается полностью, в то время как предыдущая|предварительная| уменьшается у q раз и т.п. Потому|оттого| чем более старый чем дис-крет|, тем меньшее его влияние на сумму.
Теоретически в результате присутствуют все репетиции от начала кумуляции в течение произвольно длительного времени. Но влиянием старых репетиций (с учетом конечной|концевой| разрядности вычислений|исчислений|) можно пренебречь.
Верхняя границя| суммы (1.14) после каждой репетиции увеличивается и не является заранее|кпереди,наперед| заданной, как в случае равномерной кумуляции. Рассмотрим теперь свойства этого метода|.
Если подставить (1.19) к|до| (1.14), одержимо для одного кумульова-ного| дискрета|
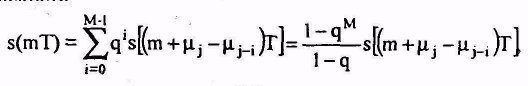(1.20)
где ( 0 (и M-1) есть начало последней (и начальной) репетиций.
Первый член в (1.17) - полезный сигнал, полученный как сумма членов геометрической прогрессии, которая|какая| с ростом М приближается к|до| своему асимптотическому значению
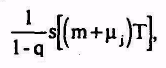(1.21)
причем отклонение от этого значения уменьшается экспоненциальное.
Можно показать, что, если такое отклонение должно составлять меньше, чем г процентов конечной|концевой| величины (3.21), необходимо кумулювати| не меньше, чем
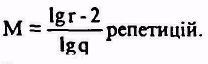(1.22)
Дисперсия случайной величины, которая|какая| является вторым членом в выражении (1.17), если считать дискрети| шуму между репетициями не коррелируемыми, имеет вид
(1.23)
Такой образом|чином|, уровень сигнала| после кумуляции М репетиций вырастет в (1 - qM)/(1 - q) раз, в то время, как эффективный уровень шума - только в [(1 — q2М)/(1 - q2)]1/2 раза. Для струма| или напряжений отношения сигнал/шум вырастет в среднем
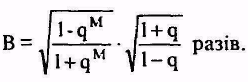(1.24)
Это значение растет|вырастает| с ростом М и для М —» °° приближается к|до|
[(1 + q))/(1 - q)1/2
Ясно, Іцо| наибольшее значение, которое|какое| можно достичь, определяется выбором коэффициента я. Чем я ближе к|до| единице, тем большего улучшения можно достичь, но тем дольше продолжается приближение к|до| постоянному|устоявшемуся| значению. Если экспоненциальная кумуляция должна дать те же значения, что и равномерная с Мо репетициями, то в соответствии к|до| (1.24)
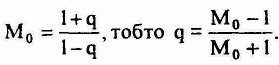(1.25)
На рис.9 приведено|наведено| сравнение результатов равномерной кумуляции с Мо = 100 и экспоненциальной 3 q = 0,980198 (в соответствии к|до| (1.22)).
Из|с| верхнего рисунка| видно снижение кумуляции, начиная с 201-ї| репетиции. При М = 100, когда равномерная кумуляция дает уже полный уровень сигнала и в среднем обеспечивает полное увеличение отношения сигнал/шум, экспоненциальная кумуляция достигает около|порядка| 86 % для обоих параметров рис.1.13.
Сейчас|в настоящий момент| уже ясно, почему экспоненциальную кумуляцию вообще используют. Она позволяет долгосрочное исследование медленных динамических|динамичных| изменений|смен| кумульованого| сигнала| без существенных технических осложнений|усложнений|. Потому|оттого| сумму (1.20) можно считать за такую, которая|какая| изменяется во времени (пульсирует), причем старые значения не отбрасываются|откидываются| после М репетиций, как это имеет место при равномерной кумуляции, а "забываются" постепенно. Как видно с рис.9 динамические|динамичные| свойства равномерной и экспоненциальной кумуляции" не очень различаются.
Экспоненциальная кумуляция реагирует на смены быстрее, но медленнее достигает постоянных|устоявшихся| значений. Достигнутый рост отношения сигнал/шум не намного хуже, чем у равномерной кумуляции.
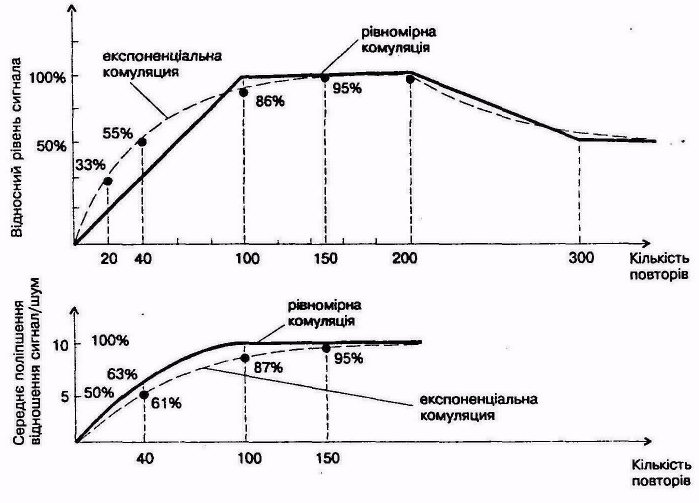
Рисунок| 9- Кумуляции с экспоненциальными изъянами|пороками|
Лекция 3-4