Кусочно-линейная аппроксимация сигнала|
Для кусочно-линейной аппроксимации сигнала| существует много разных|различных| методов, которые|какие| отличаются возможностями оптимизации изъяна аппроксимации. Как пример|приклад| наведем|приведем| алгоритм Томека (неоптимизационный) и алгоритм разделения и объединения звеньев (оптимизационный).
Алгоритм Томека
Как и в случае метода| АZТЕС интерполяция определяется исходной точкой аппроксимированного звена и разрешенным изъяном аппроксимации К. Уздовж заданного сигнала проводятся две параллельных линии, которая|какая| выходит из|с| точек S0 + К/2 и S0 – К/2 (S0 - значение выходного дискрета| інтервала| аппроксимации). Эти параллельные линии размещены таким образом, чтобы одна из них почти касалась|прикасалась|, а другая пересекала сигнал в якнайдальше| отдавании» точке от начала аппроксимации (рис.4,а).
Алгоритм можно описать следующими шагами (рис.4,б):
установление исходных точек n-го интервала - в месте начального дискрета| S0 n-го интервалу образуем две вспомогательных исходных точки со значениями Ао+ = S0 + К/2 и Ао- = S0 – К/2;
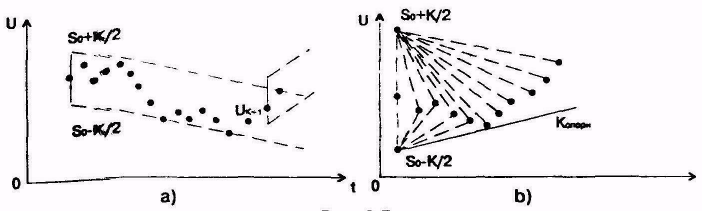
Рисунок| 4- Алгоритма Томека
2) установление направлений отрезков, которые выходят из|с| точек А0+ и А0- и перетииають| точку Si в соответствии с уравнениями
(1.10)
Эти направления считаем опорными, то есть
(1.11)
3) определение направлений отрезков, которые соединяют|сочетают| точки Ао+ и Ао-поступово с каждым і-м| с дискретів| сигнала| в аппроксимированном интервале (и = 2.....) в соответствии с уравнениями
(1.12)
4) если Кі+ > Кгеf+, тогда Кгеf+ = Кі+
если Ки- < Кгеf-, тогда Кгеf- = Ки- ;
5) если Кгеf- - Кгеf+
0, тогда переход к|до|
шагу (3);
6) окончание аппроксимации n-го интервала (параметры отрезку, что аппроксимируется, приведенные|наведенные| положением исходной точки S0 но|да| конечной|концевой| точкой n-го інтервала|, которая|какая| определена точкой 5м).
Дискрет Si-1 является одновременно начальным дискретом| следующего (n+1) -го интервала аппроксимации;
7) если аппроксимирован весь сигнал, вычисление|исчисление| заканчиваем, если нет - возвращаемся|поворачиваемся| на шаг (1) алгоритме|.
Алгоритм разделения и объединения интервалов
В этом алгоритме| есть оптимизационная процедура, при которой|какой| выполняется|исполняется| как можно лучше аппроксимация данной кривой по частям ломаной линией.
Погрешность аппроксимации можно определить разными способами (среднее квадратичное отклонение, максимальное отклонение, и тому подобное). В случае сигнала| ЭКГ удобно критерием (который|какой| не имеет интегрального характера) выбрать|избрать| именно максимальное отклонение.
Алгоритм разделения и объединения интервалов соединяет|сочетает| выполнение двух условий оптимизации:
1) для данного количества сегментов найти такие узлы Uk (точки преломления), чтобы погрешность аппроксимации была минимальной;
2) для данной величины погрешности провести аппроксимацию ломаной линией так, чтобы количество сегментов аппроксимации было самым малым.
Алгоритм выходит из|с| начальной аппроксимации, которую|какую| можно образовать, например, предыдущим|предварительным| алгоритмом Томека. Последующие действия алгоритма можно описать следующими шагами:
1) деление сегментов. Если изъян аппроксимации на некотором|некоем| интервале больший, чем разрешенное предельное значение, этот сегмент делят на два. Новый узел размещают в месте максимального отклонения отрезку, что аппроксимируется, от выходного сигнала|. Если эта координата неизвестна, сегмент делят на две равных части. Этот шаг заканчивается, если разделены все сегменты с большим|великим| изъяном;
2) соединение сегментов. Оценивают изъян аппроксимации при объединении двух соседних сегментов к|до| единственному|единому|. Если она не превышает разрешенные границы|черты|, сегменты объединяются отбрасыванием узла между ними. Второй шаг заканчивается объединением всех сегментов, изъян которых|каких| это позволяет;
3) оптимизация положения узлов (рис.5). Вычисление|исчисление| проходит в двух фазах. В первой фазе оптимизируют положение парных|четных| узлов (между 1 и 2-м сегментами, 3 и 4-м сегментами ...). Во второй фазе - положение непарных|нечетных| узлов (между 2 и 3-м сегментами и тому подобное). В каждой фазе сравниваются изъяны аппроксимации в соседних сегментах. Если где-то она наибольшая, тогда узел подвигают на данное количество т дискретів| так, чтобы сегмент с большим изъяном сократился, а сегмент с меньшим изъяном продлился|удлинился|. После перемещения узлов вычисляют|исчисляющий| апроксимаційну| изъян в обоих сегментах, которые опять|снова| появились. Если больший изъян (из|с| двух новых изъянов аппроксимации для двух новых сегментов) является меньше, чем большая из|с| двух предыдущих|предварительных| изъянов, посунення| узла дало ожидаемый позитивный|положительный| эффект, и вычисления|исчисления| продолжают для последующей пары сегментов, иначе - узел возвращается|поворачивается| к|до| исходному|выходному| значению. По рассмотрении всех парных|четных| узлов та же процедура повторяется действие всех непарных|нечетных| узлов.
Рисунок| 5- Алгоритма разделения и о` единение интервалов
Третий шаг повторяют так долго, пока благодаря подвиганию узлов уменьшаешь» погрешность аппроксимации. Количество дискретів|, на которые|какие| узел при расчетах подвигается, в большинстве случаев удобно принимать m = 1, особенно|в особенности| тогда, когда начальная аппроксимация находится вблизи оптималиюго| решения.
Серия из|с| описанных трех шагов тоже повторяется так долго, пока приносит позитивные|положительные| изменения|смены|. Если в серии из|с| этих трех шагов уже не изменяется положение узлов, тогда решение задачи оптимизации прекращается.