13 Схемы сравнения цифровых кодов

13.1 Общие положения

Схемы сравнения кодов довольно часто встречаются в промышленных цифровых приборах, устройствах вычислительной техники, измерительных системах и служат для выявления соответствия некоторого значения цифрового кода заданному уровню. Схемы сравнения кодов условно можно разделить на две группы:

– выявляющие совпадение кодов;

– выявляющие большее число.

Схемы, выявляющие совпадения кодов, должны обеспечить выходной сигнал, равный единице, только в случае полного совпадения сравниваемых кодов. Сравниваться могут числа, заданные в двоичном и двоично-десятичном коде, имеющие одинаковое количество разрядов: А = А_n…А₂А₁А₀, В = В_n…В₂В₁В₀. Совпадение кодов означает равенство чисел во всех разрядах:

А_n = В_n, …, А₂ = В₂, А₁ = В₁, А₀ = В₀.

При сравнении двух одноразрядных кодов можно не составлять таблицу истинности, поскольку для совпадения кодов достаточно, чтобы оба разряда были равны нулю либо единице. Такую функцию реализует схема равнозначности: = А_i  В_i, а ее инверсивное значение имеет функция неравнозначности («исключающее ИЛИ»): , т.е. сумма по модулю два.

При равенстве кодов реализуется функция … , преобразуя которую по правилу де Моргана (отрицания), получим

.

Последнее выражение можно реализовать с помощью логических схем «исключающее ИЛИ» и схемы ИЛИ (рисунок 13.1). За основу взята МСХ К133ЛП5 (555, 1531, 1533 и др.), содержащая четыре 2-х входовых элемента «исключающее ИЛИ» и 4-х входовой логический элемент ИЛИ-НЕ (половина ИС К155ЛЕ3). Логический элемент ИЛИ-НЕ имеет дополнительный вход разрешения приема сигнала EI (Enable Input). Управляющий сигнал на этом входе разрешает (или запрещает) прием сигнала по каждому входу ЛЭ.

Построение схемы, выявляющей большее (или меньшее) из двух сравниваемых чисел, рассмотрим на примере сравнения двух двоичных чисел А = А_n…А₂А₁А₀, В = В_n…В₂В₁В₀. Схема должна обеспечить на выходе сигнал N, равный единице в случае, когда A > B. Если же А  В, то сигнал на выходе такой цепи должен быть равен нулю. Для получения логической функции, которую должна реализовать схема, нужно взять за основу ячейку, сравнивающую одноразрядные коды. При этом очевидно что A_i > B_i, если A_i =1 и B_i = 0, т.е. .

Многоразрядные числа следует сравнивать следующим образом. Вначале сравнивают коды в первом, старшем разряде. Если А_n > B_n, следовательно, , и сразу можно сделать вывод, что независимо от содержания младших разрядов

АВ. Если же в первом разряде коды совпадают, то и нужно перейти к анализу следующего разряда. Если в следующем разряде A_n–1>B_n–1, тогда 1 и, следовательно, А>B. Если же в этом разряде A_n-1 = B_n-1, то с учетом равенства бит старшего разряда получим промежуточный результат:

.

Рассуждая таким образом, получим:

; ; …

; .

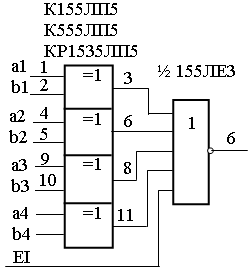
Рисунок 13.1 – Cхема cравнения кодов на равенство

Если хотя бы одно значение окажется равным единице, то на выходе дизьюнктора установится высокий уровень, указывающий на то, что А>В.

Сигналы R_i, полученные по ходу решения задачи, можно использовать для реализации функции R, указывающей на равенство кодов. Если буквой М_i обозначить функцию, принимающую уровень лог.1 при А_i < В_i ( ), то формулу для R_i можно записать в следующем виде:

.

Это означает, что R_i = 1 в том случае, когда a_i = b_i.

Реализовать устройство, выявляющее большее число, можно на ЛЭ низкой степени интеграции, хотя в этом нет необходимости, поскольку в разных сериях имеются цифровые четырехразрядные компараторы. Примером могут служить микросхемы К564ИП2, К555СП1, К531СП1 (ТТЛШ), выпускаемые отечественной промышленностью.

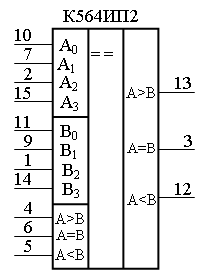
Рисунок 13.2 – Условное графическое обозначение

ИС К564ИП2