12 Арифметические устройства

12.1 Комбинационные двоичные сумматоры

Сумматор – это узел, в котором выполняется арифметическая операция суммирования цифровых кодов двух двоичных чисел. Числа в любой позиционной системе счисления складываются поразрядно. Поэтому сложить двоичные числа можно при наличии узлов, реализующих суммирование цифр одного разряда слагаемых с учетом возможного переноса из соседнего младшего разряда. К таким узлам относят одноразрядные комбинационные полусумматоры и сумматоры.

Комбинационный полусумматор HS предназначен для суммирования двух одноразрядных двоичных чисел. Он имеет два входа , и , два выхода – S_i и P_i+1. Выход S_i является выходом суммы, а выход P_i+1 – выходом переноса.

На основании таблицы 12.1 переключательные функции для S_i, и P_i+1 в СДНФ будут иметь следующий вид:

Полусумма является функцией неравнозначности входных сигналов и («исключающее ИЛИ» )

, (12.1)

которая инверсна по отношению к функции равнозначности

. (12.2)

Таблица 12.1

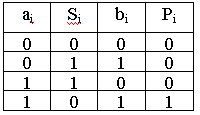
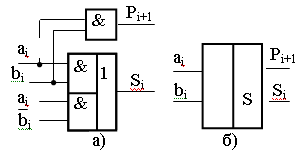
Рисунок 12.1 – Полусумматор: а − функциональная схема;

б − условное графическое изображение

Устройство можно реализовать на логических элементах И, ИЛИ (рисунок 12.1). Основным требованием, предъявляемым к нему, является получение максимального быстродействия при минимальном числе последовательно включенных элементов.

Одноразрядный комбинационный сумматор предназначен для суммирования трех одноразрядных двоичных чисел. Он имеет три входа: , , и два выхода: S_i и P_i+1. На входы и поступают значения суммируемых цифр данного разряда, на вход – значение переноса из соседнего младшего разряда. Порядок переключения трехвходового сумматора представлен в таблице 12.2, условное графическое обозначение на рисунке 12.2. На основе таблицы истинности (таблица 12.2) переключательные функции в СДНФ для S_i и P_i+1 будут иметь следующий вид:

Таблица 12.2

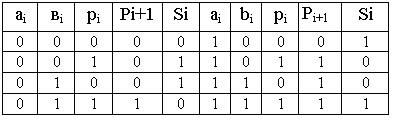
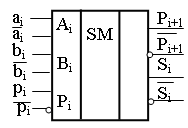
Рисунок 12.2 – Одноразрядный комбинационный сумматор

Минимизируем полученные выражения с помощью карт Карно (рисунок 12.3). Анализ таблицы для S_i показывает, что переключательная функция упрощению не поддается. Тогда преобразуем это выражение с помощью правил алгебры логики. Объединим первый и четвертый, второй и третий минтермы, а их общие сомножители (P_i и ) вынесем за скобки:

.

С учетом (12.1) и (12.2) это выражение запишется в виде .

Оригинальное выражение для суммы S_i можно получить непосредственно из таблицы 12.2

.

Минимизированное логическое выражение для результата переноса в следующий разряд P_i+1 найдем по карте Карно:

P_i+1 = a_i b_i + a_i P_i + b_i P_i = a_i b_i + P_i (a_i + b_i).

Введем обозначения:

G_i = a_i b_i и T_i = (a_i + b_i),

получим

P_i+1 = G_i + P_i T_i.

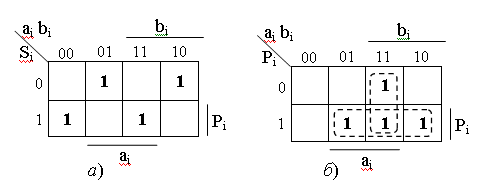
Рисунок 12.3 – Карты Карно: а − переключательных функций S_i; б − переключательных функций P_i

Функцию G_i называют функцией генерации (формирования) поразрядного переноса i-го разряда, а T_i – функцией передачи (распространения) переноса для i- го разряда. Реализация устройства суммирования трехразрядного сумматора может выполняться как показано на рисунке 12.4.

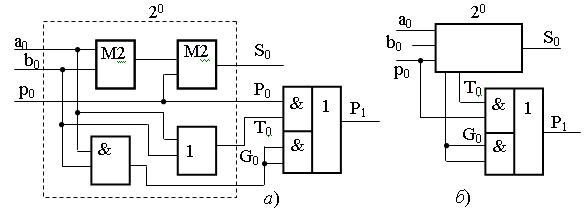
Рисунок 12.4 – Сумматор: а − одноразрядный сумматор; б− упрощенное изображение

МикросхемаК555ИМ5 – два одноразрядных полных сумматора. Она выполняет операцию сложения трех одноразрядных чисел в двоичном коде с учетом переноса младшего разряда в старший (рисунок 12.5).

Состояние выходных уровней схемы в зависимости от состояний на входах , и соответствует показанным в таблице 12.2.

Высокий и низкий уровни сигнала на выходах схемы S_n и P_n+1 устанавливаются при наличии высокого и низкого уровней на всех входах микросхемы.

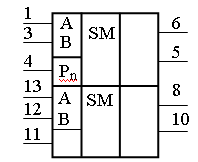
Рисунок 12.5 – Условное графическое изображение ИС К555ИМ5