3.6.2 Минимизация логических функций с помощью карт Карно

Метод минимизации карт Карно (Вейча) находит широкое применение для минимизации переключательных функций 3 – 6 аргументов, поскольку обеспечивает простоту получения результата. На рисунке 3.5, а, б, в приведены карты Карно для трех f (x₃ x₂ x₁), четырех f(x₄ x₃ x₂ x₁) и пяти аргументов f(x₅ x₄ x₃ x₂ x₁) с нанесенными на них номерами минтермов функции f(x₄ x₃ x₂ x₁), где x₅ – старший разряд, x₁ – младший. Аргументы функции делятся на две группы, комбинации значений аргументов одной группы приписываются столбцам таблицы, комбинации значений аргументов другой группы – строкам таблицы. Столбцы и строки обозначаются комбинациями, соответствующим последовательности чисел в коде Грея, поскольку в этом случае склеивающиеся клетки находятся рядом.

Карта Карно определяет значение функции на всех возможных наборах аргументов и, следовательно, является таблицей истинности. Карты Карно компактны и удобны для поиска склеиваемых членов переключательной функции СДНФ. Объясняется это тем, что два любых минтерма, находящихся в клетках, расположенных рядом друг с другом, являются соседними. Они могут быть заменены одной конъюнкцией, содержащей на одну переменную меньше.

Группа из четырех минтермов, расположенных в соседних клетках, может быть заменена конъюнкцией, содержащей на две переменные меньше. В общем случае группа из 2^k соседних клеток будет заменена одной конъюнкцией с n – k аргументами, при общем числе переменных равным n.

Минимизацию переключательных функций будем вести на основании следующих правил:

– все клетки, содержащие 1, объединяются в замкнутые области;

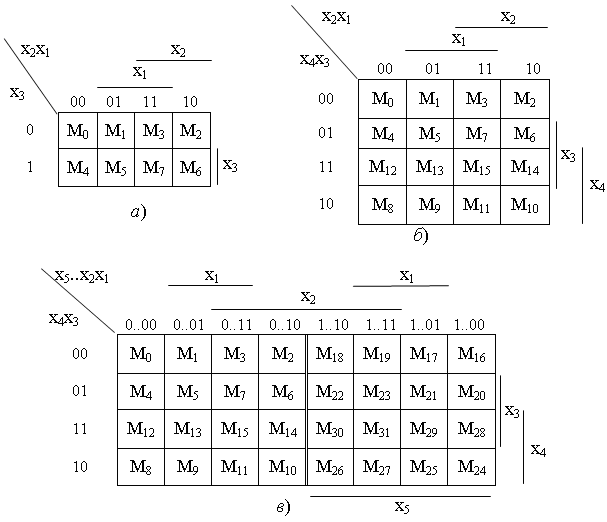
Рисунок 3.5 − Карты Карно для: а −3-х аргументов; б − 4-х аргументов; в − 5-ти аргументов

– каждая область должна представлять собой прямоугольник или квадрат с числом клеток 2^k;

– клетки, расположенные на противоположных гранях таблицы, являются соседними, так как карту можно сворачивать в цилиндр по горизонтали и по вертикали;

– угловые клетки, расположенные на противоположных углах, являются соседними, в том числе все четыре угловые клетки объединяются в одну область;

– области могут пересекаться и одни и те же клетки могут входить в разные области;

– клетки, значение функции в которых не определено (Ф), могут принимать любое значение (0 или 1);

– необходимо стремиться к тому, чтобы число областей было минимальным, а каждая область содержала возможно большее число клеток.

На рисунке 3.6 – 3.8 приведены карты Карно с нанесенными на них различными вариантами переключательных функций.

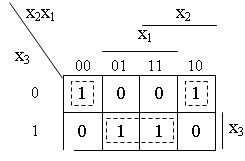
Рисунок 3.6 − Карты Карно для 3-х переменных

На рисунке 3.6 приведена карта Карно для функции трех переменных

у = М₀ М₂ М₅ М₇.

В исходную функцию входят 12 переменных, необходимо минимизировать эту функцию. Объединим попарно клетки с минтермами М₀ и М₂, М₅ и М₇, поскольку они являются соседними. В первом случае в исходную функцию прямо и инверсно входит х₁ и, следовательно, эта переменная будет исключена из конечного выражения. Для второй пары минтермов такой переменной будет х₂, которая также будет исключена из конечного выражения. Минимизированная функция запишется в виде . Полученное выражение является функцией равнозначности

y = x₁ x₃.

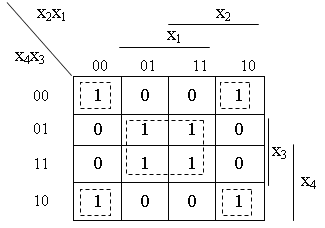
Рисунок 3.7 − Карты Карно для 4-х переменных

На карту, приведенную на рисунке 3.7, нанесена функция четырех аргументов:

у = М₀ М₂ М₅ М₇ М₈ М₁₀ М₁₃ М₁₅.

Угловые минтермы М₀, М₂, М₈, М₁₀ являются соседними, т. к. карту можно сворачивать как по горизонтали, так и по вертикали. В эти четыре минтерма прямо и инверсно входят переменные х₂ и х₄, поэтому они не войдут в минимизированное выражение. Минимизированное выражение для этих минтермов

у₁ =

Остальные четыре минтерма М₅, М₇, М₁₃, М₁₅ образуют замкнутую область в виде квадрата. Из конечного выражения здесь также будут исключены переменные х₂ и х_4. Минимизированное выражение для квадрата запишется в виде: у₂ = х₁ х₃.

Результирующее выражение

или y = x₁ x_3.

Рассмотрим пример минимизации логической функции пяти аргументов.

Пусть задана некоторая функция

У = М₂ М₃ М₄ М₅ М₁₀ М₁₁ М₁₂ М₁₃ М₁₈ М₁₉ М₂₀ М₂₁ М₂₂ М₂₆ М₂₇ М₂₈ М₂₉ М₃₀.

Нанесем ее на карту Карно (рисунок 3.8).

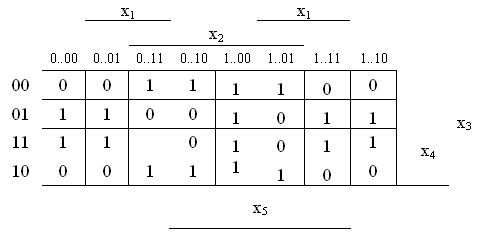
Рисунок 3.8 − Карты Карно для 5-ти аргументов

Выделим четыре области, объединяющие соседние клетки:

– первую область образуют клетки:

у₁ = М₄ М₅ М₁₂ М₁₃ М₂₀ М₂₁ М₂₈ М₂₉;

– вторая область образована клетками:

у₂ = М₂ М₃  М₁₀ М₁₁  М₁₈ М₁₉ М₂₆ М_27;

– третья область: у₃ = М₁₈ М₂₂ М₂₆ М₃₀.

Для первой области минимизированное выражение будет равно ,для второй области выражение – , третья область будет описываться логической функцией .

Минимизированное результирующее выражение будет равняться логической сумме полученных выражений:

.

В исходное логическое выражение входило восемьдесят аргументов, а в конечное минимизированное выражение – всего лишь семь. Отсюда следует вывод, что использование карт Карно для минимизации логических функций весьма эффективно. Причем исходная логическая функция может быть не полностью определена на всем набор и может не иметь совершенной дизъюнктивной нормальной формы.

Например, необходимо спроектировать дешифратор, лог.1 на выходе которого будет устанавливаться при поступлении на вход десятичного счетчика четвертого, пятого, шестого и седьмого импульсов у = М₄ М₅ М₆ М_7.

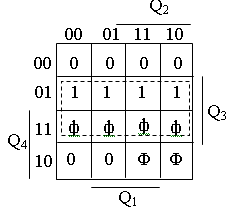
Рисунок 3.9 – Карта Карно для функции М₄ – М₇

Воспользуемся картой Карно для четырех переменных (рисунок 3.9). Нанесем на нее указанную функцию в виде четырех единиц. В клетки с номерами минтермов с 10 по 15 внесем значение функционала – Ф, т. к. у десятичного счетчика эти позиции отсутствуют. Объединим в одну область все единицы и одну строку функционалов (всего восемь клеток). Эта область опишется функцией y = Q₃. Полученное выражение показывает, что для решения задачи не требуется внешний дешифратор. Функция автоматически формируется на выходе третьего триггера: Y = Q₃.