1.4. Поняття про вейвлет-перетворення
Вирішити певною мірою проблему одночасної високої роздільної здатності як по частоті так і по часу може, так зване, вейвлет-перетворення.
За визначенням неперервне вейвлет-перетворення можна записати у вигляді
,
(1.26)
де
– функція перетворення, яка має назву
материнського вейвлета,
– кофіцієнт масштабу або просто масштаб.
Слово вейвлет можна перекласти як маленька хвиля. Під словом маленька розуміють те, що така віконна функція має кінцеву ширину. Слово хвиля вказує на той факт, що віконна функція – осцилююча функція. Термін материнський озночає, що різні за шириною віконні функції, які використовуються у перетворенні народжуються від однієї і тієї базової функції – материнського вейвлета.
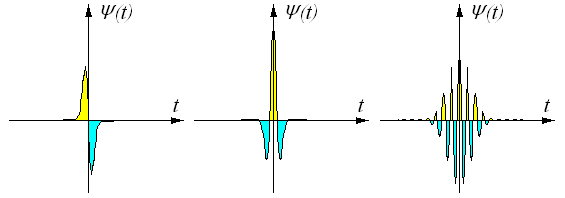
а б в
Рис. 1.13
а – WAVE-вейвлет; б – MHAT-вейвлет (мексиканський капелюх); в – вейвлет Морле
Вейвлети можуть бути різної конфігурації (див., рис. 1.13). Головна вимога до вейалету така
.
(1.27)
Оскільки вейвлет осцилююча біля нуля функція, то геометричне тлумачення виразу 1.27 означає – площа ділянок обмежених позитивними і негативними ділянками вейвлета однакова.
Відзначимо, що для вирішення конкретної задачі аналізу сигналу існує оптимальна конфігурація вейвлета, вибір якої є далеко не простим.
Якщо звернути увагу на визначення вейвлет-перетворення, то можна побачити, що вейвлет-образ є функцією масштабу. Параметр може бути як більше так і менше одиниці, тобто віконна функція стискається або розширюється у відповідності до . Інакше кажучи для кожного моменту часу існує ціла сукупність образів, отриманих для різних . Саме завдяки цьому вейвлет-перетворення дає змогу детально проаналізувати поведінку сигналу у часі.
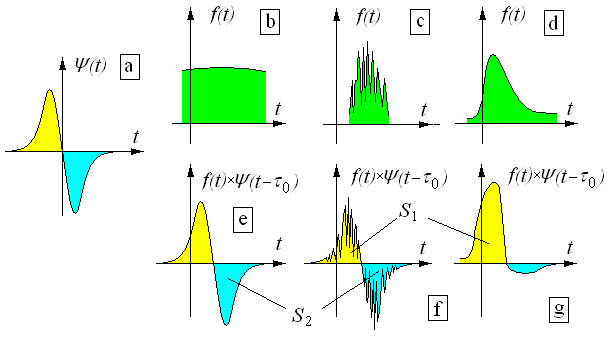
Рис. 1.14. До пояснення ідеї Вейвлет аналізу
a
– вейвлет певного масштабу; b-d
– ділянки сигналу з різним масштабом
флуктуацій. b
– ділянка сигналу де характерний
тривалість елементу сигналу значно
більша ніж ширина вейвлету; с
– ділянка сигналу де характерна
тривалість елементу сигналу значно
менша ніж ширина вейвлету; d
– ширина вейвлету сумірна за розмірами
з елементом сигналу; e-g
– результати множення вейвлета на
сигнал з різним масштабом флуктуації.
– позитивна та негативна площі результату
множення.
Спробуємо пояснити ідею вейвлет-перетворення виходячи з наступних міркувань. Згідно до визначення вейвлет-перетворення для розрахунку образу необхідно здійснити такі операції:
1.
Вибрати величину масштабу
.
Відзначимо, що розрахунок образу
починається із значення
.
Далі величина
змінюється як в бік більше одиниці
(«вузькі» вейвлети), так і бік
менше одиниці («широкі» вейвлети).
2.
Зсунути вейвлет з масштабом
на певну
.
3. Перемножити віконну функцію та сигнал. Природно, що певної внличини добутку можна очікувати лише в інтервалі порівнянному з шириною вейвлета.
4. Провести інтегрування добутку.
Нехай
ми маємо материнський вейвлет, подібний
до зображеного на рисунку 1.14а
і
для певного
цей вейвлет займає позицію відносно
сигналу таку, як зображено на рисунку
b.
Оскільки на ділянці в районі
сигнал практично постійний, то маємо
результат множення віконної функції
на сигнал подібний до зображеного на
рисунку e.
Природно, що такому випадку результат
інтегрування наближається до нуля.
Величина «позитивних» площ
приблизно дорівнює величіні «негативних»
площ
.
Аналогічний результат ми отримаємо і в випадку, коли вейвлет зсунутий в район сигналу, де він має структуру меншу за масштабом ніж вейвлет (див. рис. с).
І лише у випадку, коли вейвлет знаходиться в околі точки, де сигнал має масштаб флуктуацій близький до ширини віконної функції результат інтегрування буде суттєво відрізнятися від нуля. Таким чином відмінність від нуля образу в певній точці для певної величини свідчить про те, що саме тут сигнал має флуктуацію з аналогічним масштабом.
Продемонструємо ефективність вейлет-перетворення на прикладі сигналу, зображеному на рисунку 1.15. Цей сигнал не стаціонарний, проте в різні інтервали часу можна виділити стаціонарні ділянки, де частота сигналу постійна:
1-ша ділянка – 30 Гц (0-300 мкс),
2-га ділянка – 20 Гц (300-600 мкс),
3-тя ділянка – 10 Гц (600-800 мкс),
4-та ділянка – 5 Гц (800-1000 мкс).
Взагалі кажучи масштабний параметр вейвлет-перетворення не можна напряму асоціювати з частотою. Тим не менш можна стверджувати – чим «дрібніша» структура сигналу, тим більш високі частоти присутні в сигналі. Природно, що для сукупності гармонійних сигналів, які не перекриваються в часі (сигнал типу, зображеного на рисунку 1.15) аналогія між масштабом флуктуації сигналу і його частотою повна. Фактично масштаб флуктуації сигналу дорівнює половині періоду гармонійного сигналу. Або інакше – масштаб обернено пропорціний до частоти. Отже аналізуючи вейвлет-образ такого сигналу можна зробити однозначний висновок не тільки про стаціонарність (або не стаціонарність) сигналу в певні інтервали часу, а й про зміну масштабу його флуктуацій, тобто зміну частоти.
Цей висновок підтверджується рисунком 1.16, на якому наданий вейвлет-образ розглянутого сигналу.
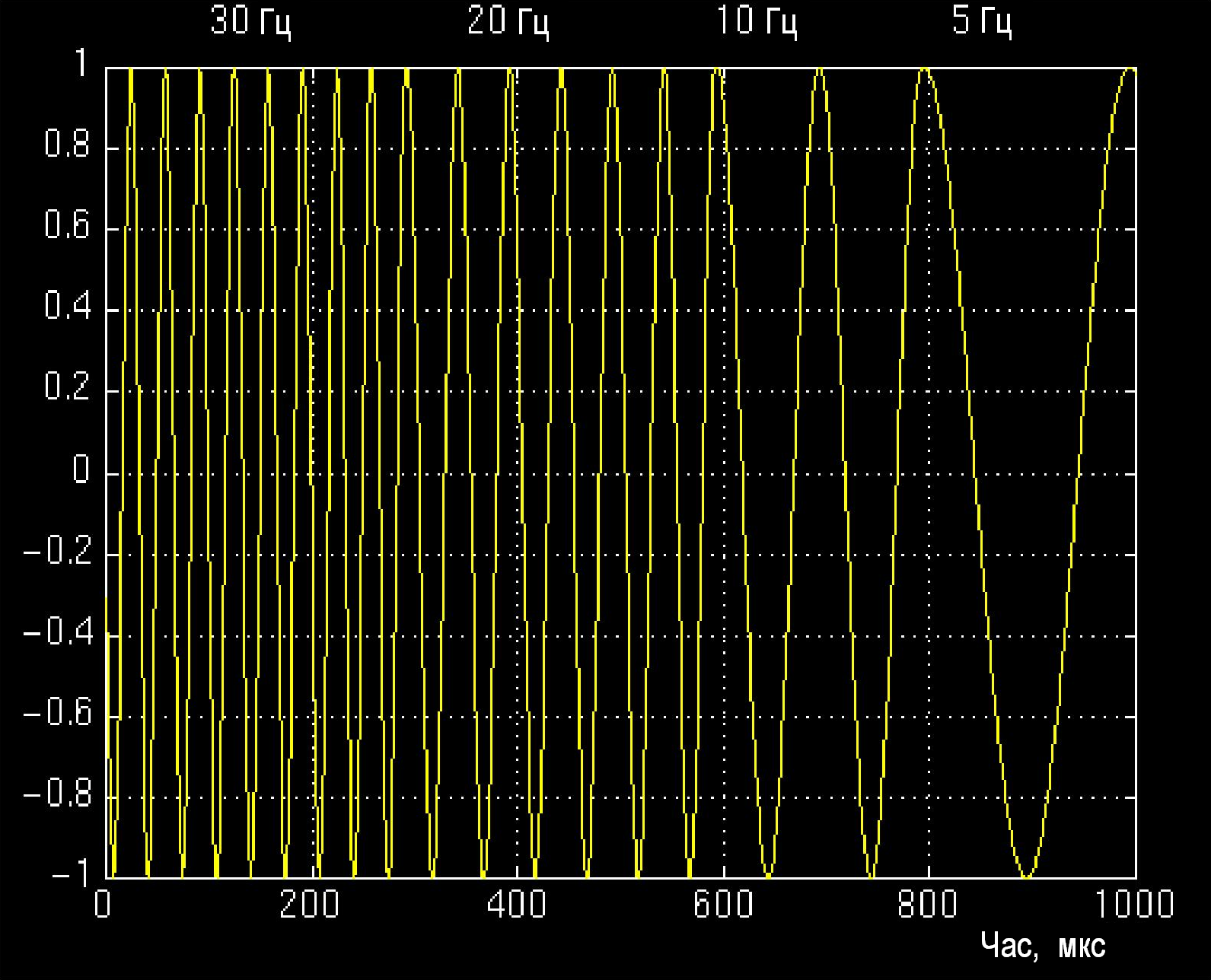
Рис. 1.15. Нестаціонарний сигнал, який складається з чотирьох стаціонарних ділянок з частотами 30 Гц (0-300 мкс), 20 Гц (300-600 мкс), 10 Гц (600-800 мкс) і 5 Гц (800-1000 мкс).
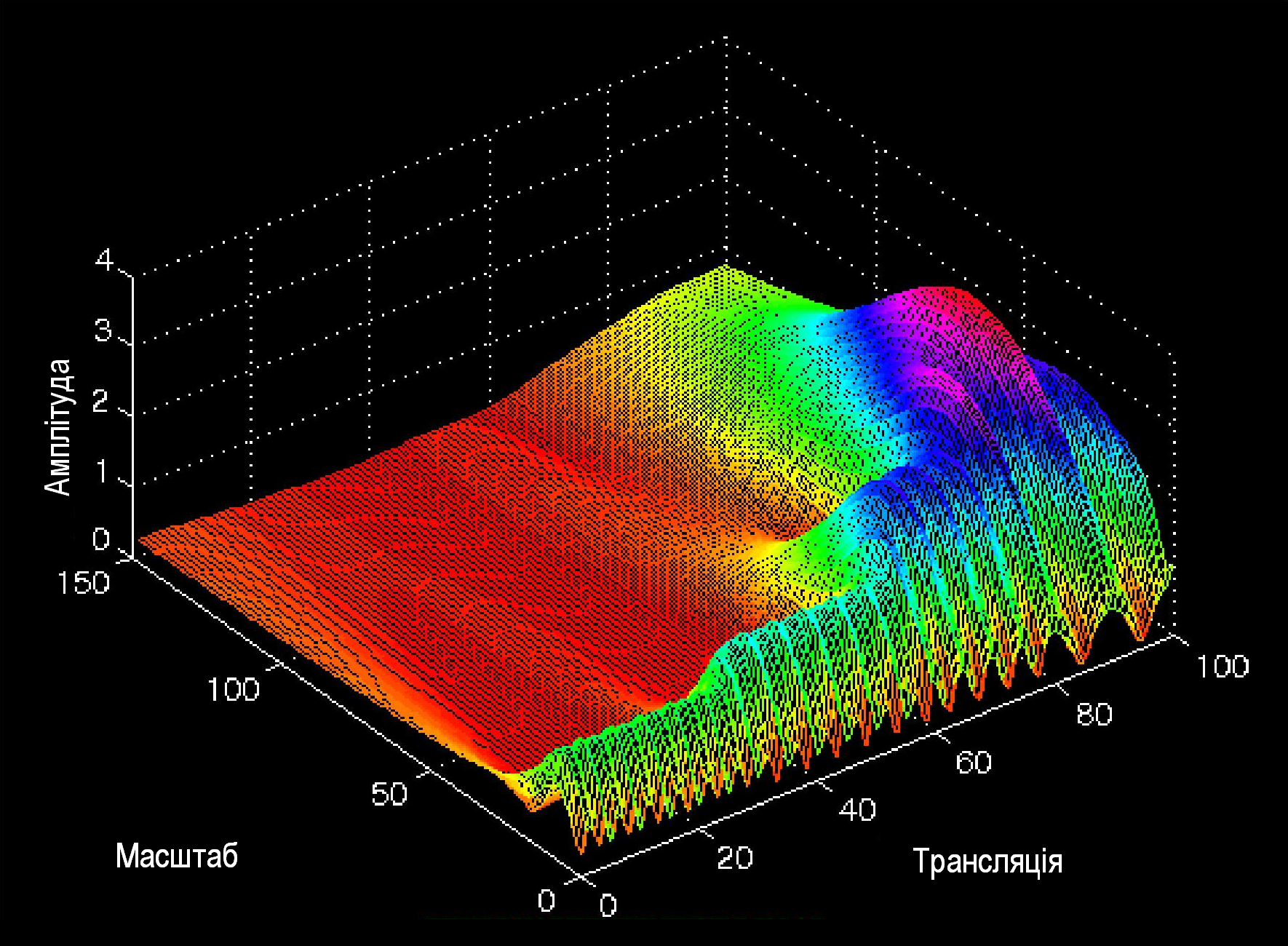
Рис. 1.16. Вейвлет-образ сигналу, зображеного на рисунку 1.15
На рисунку 1.17. наданий той самий вейвлет-образ представлений під іншим ракурсом.
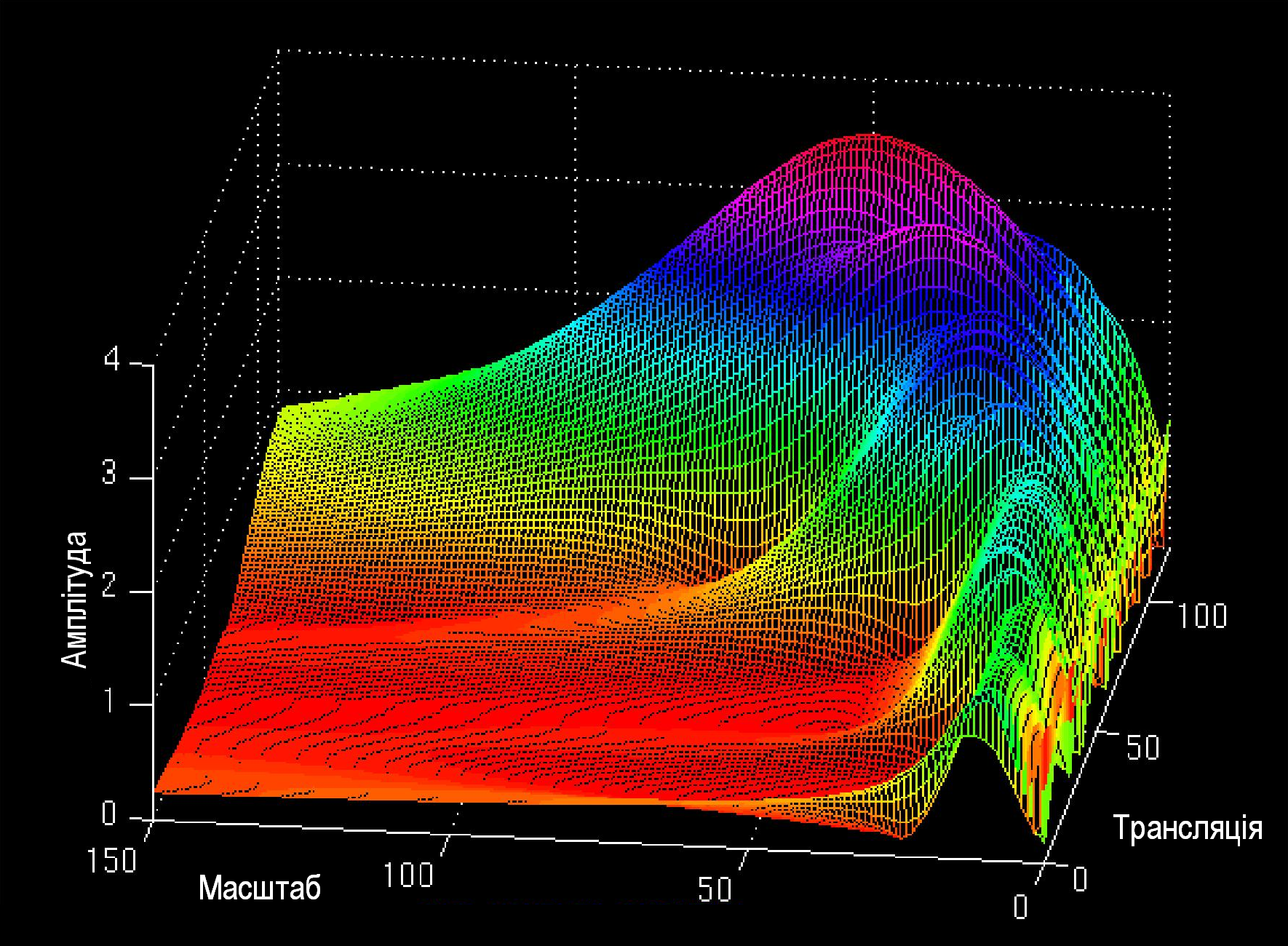
Рис. 1.17
Відзначимо, що зсув (на рисунку – трансляція) може бути асоційований з часом.
З рисунків добре видно, що спочатку в сигналі спостерігаються найменші масштаби флуктуації (висока частота), які зростають і досягають максимуму в кінці існування сигналу (частота 5 Гц).
Зауважимо, що вейвлет-перетворення, яке ми розглядали як «альтернативу» ОФП не позбавлене недоліків. Наприклад, різна роздільна здатність за часом для різних масштабів флуктуації.
Відповідно, для відносно повного аналізу сигналу бажано застосовувати всі три, розглянуті нами перетворення: Фур’є-перетворення, ОФП, та вейвлет-перетвореня.
На закінчення наведемо приклад реального застосування вейвлет-перетворення.
На рисунку 1.18 представлена певна медична характеристика здорової людини. Вейвлет-образ цього сигналу ілюструється рисунком 1.19 та рисунком 1.20 (вейвлет-образ під іншим ракурсом).
Як бачимо з рисунків 1.19 та 1.20 в області «середніх масштабів вейвлет-образ характеристики здорової людини має яскраво виражене провалля.
На рисунку 1.21. наведена характеристика людини, яка хвора на хворобу Альцгеймера. На рисунках 1.22. та 1.23. наведені вейвлет-образи.
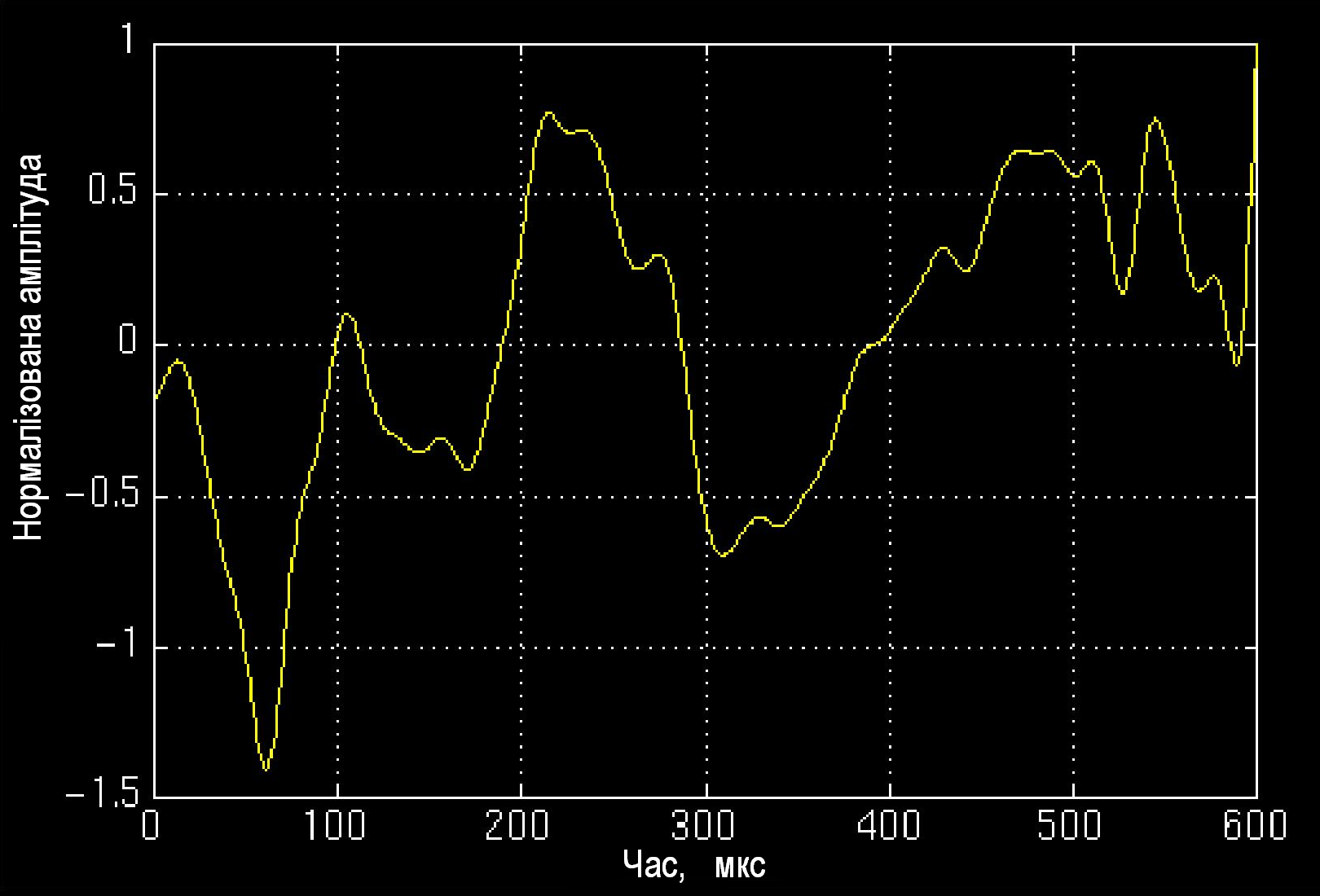
Рис. 1.18
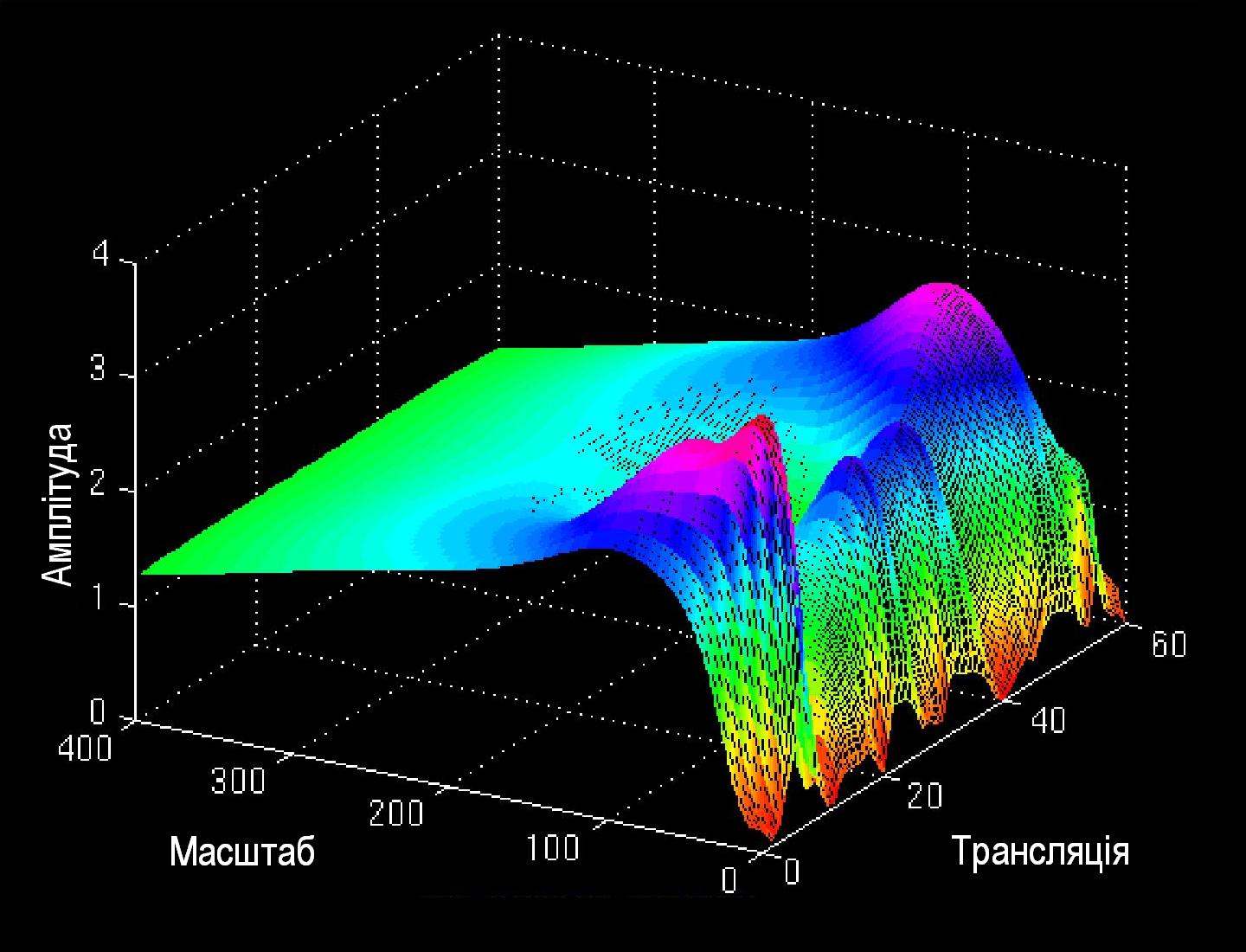
Рис. 1.19
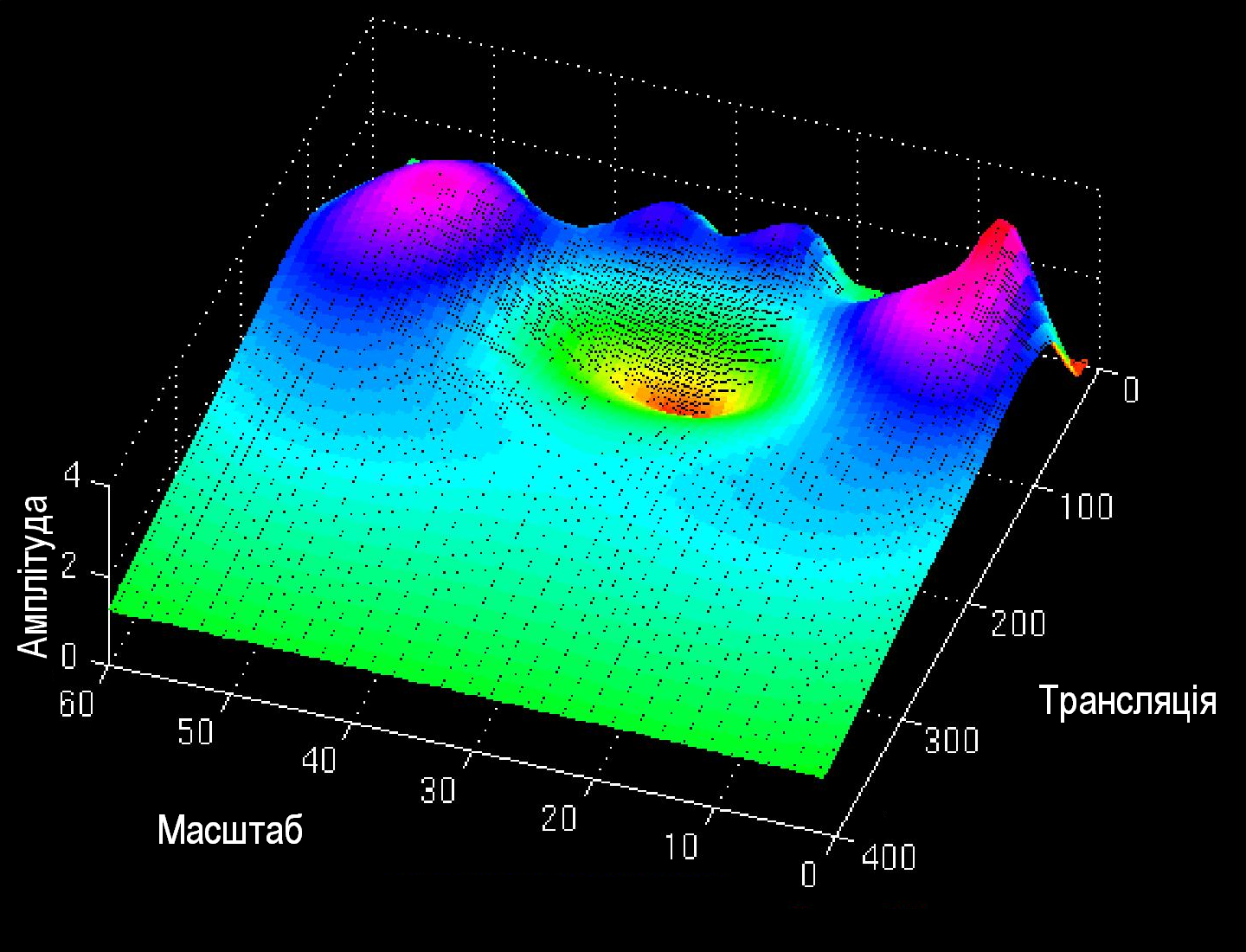
Рис. 1.20
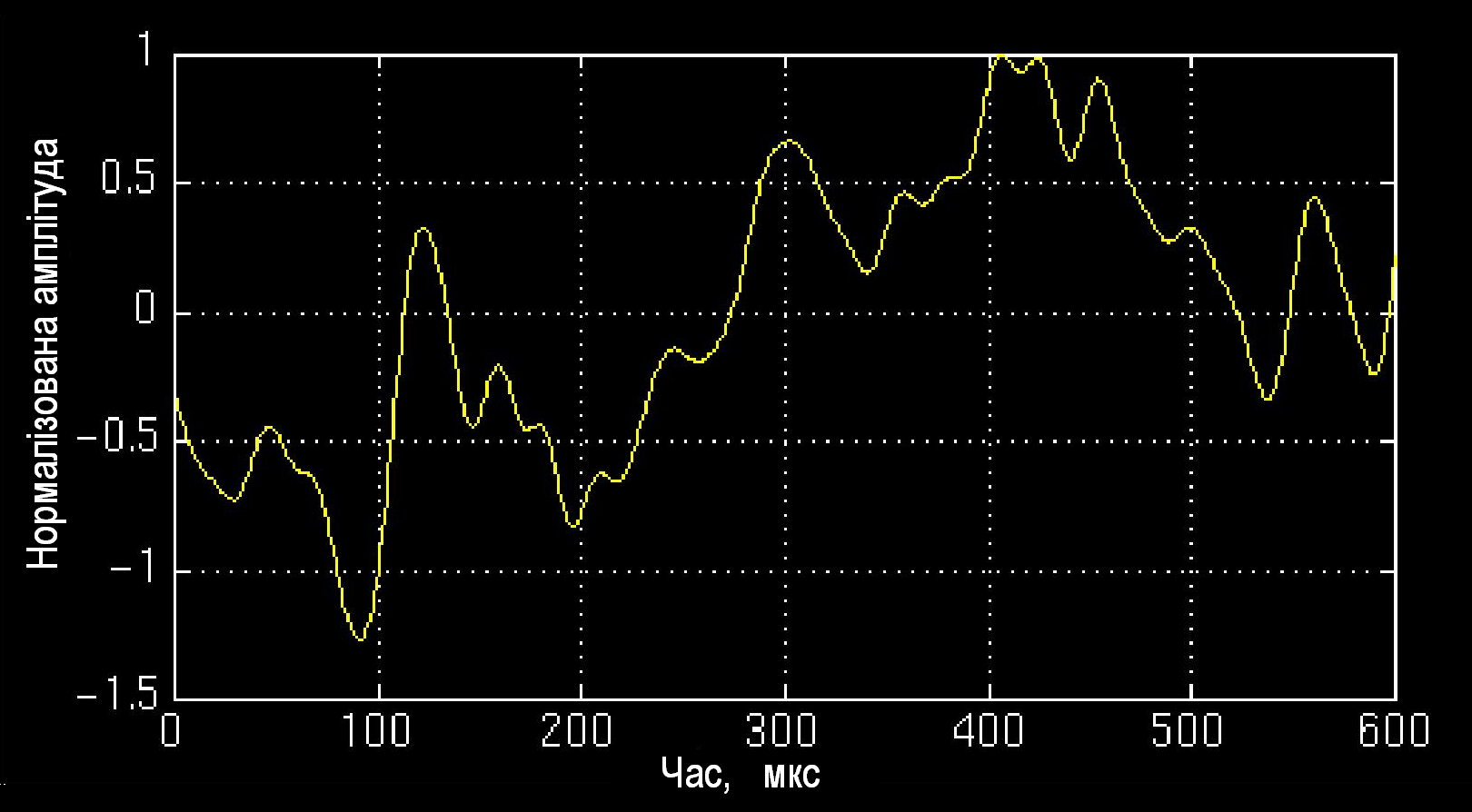
Рис. 1.21
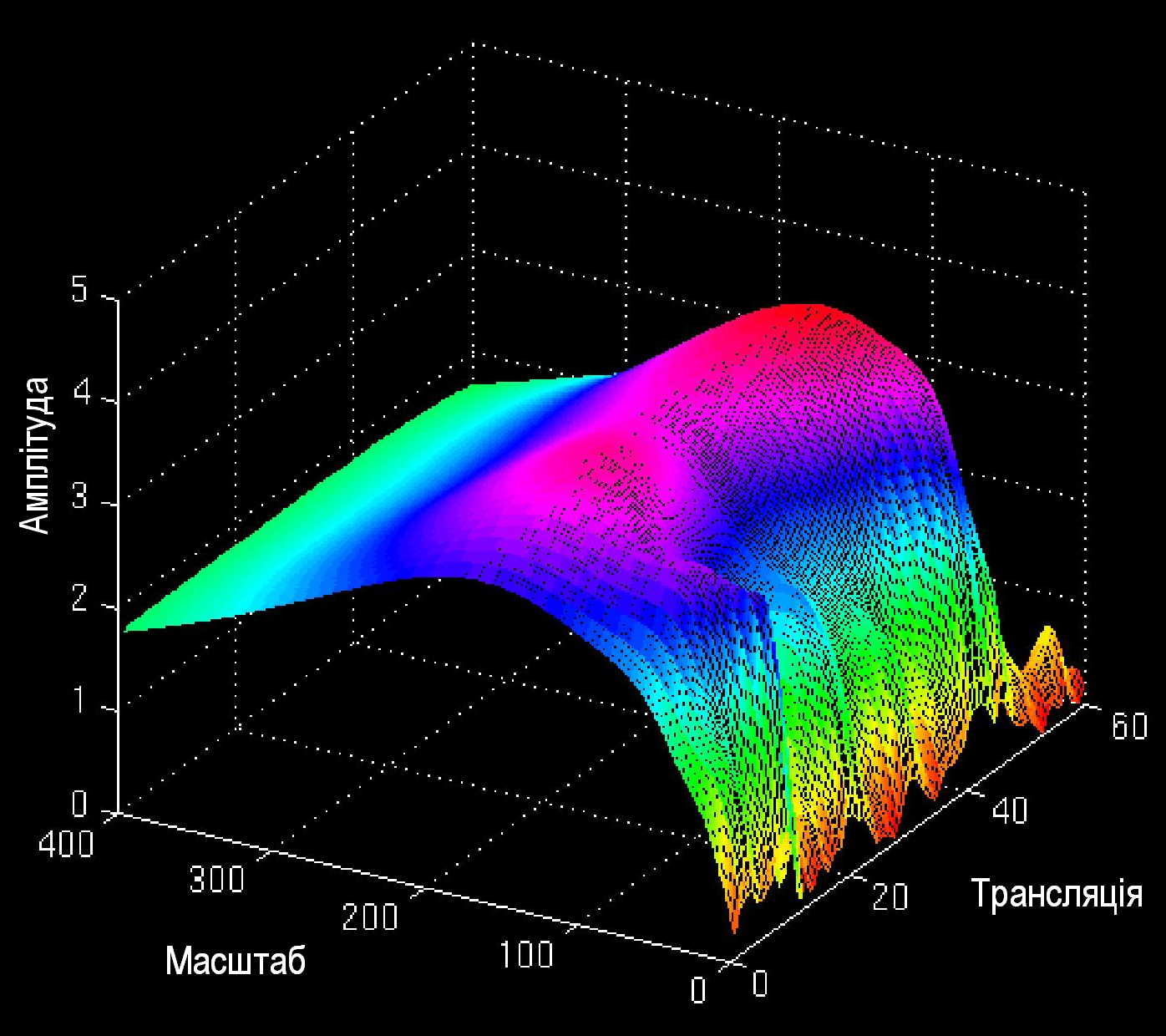
Рис. 1.22
Рис. 1.23
Треба відзначити, що порівнюючи рисунки 1.18 та 1.19 важко зробити висновки про відмінності в медичних характеристиках. Разом з тим, як читко випливає з рисунків 1.19, 1.20 та 1.22, 1.23 у хворої людини у вейвлет-образі відсутнє провалля в області середніх масштабів. Інакше кажучи, в цьому випадку, саме вейвлет-перетворення дає нам можливість однозначно встановити діагноз хвороби.