1.1.2. Деякі властивості Фур’є перетворення

Наведемо деякі важливі властивості Фур’є перетворення:

1. Лінійність перетворення Фур’є

, (1.10)

де – Фур’є образи функцій відповідно, – коефіцієнти.

Для сигналу у якому гармонійні складові такі коефіцієнти дійсні та додатні і визначають величину вкладу цієї складової в сигнал.

2. Теорема зсуву

, (1.11)

де – Фур’є образ не зсунутого сигналу, – величина зсуву

або

, (1.12)

тобто Фур’є образ зсунутої функції відрізняється від образу не зсунутої на експоненціальний множник .

Відзначимо, якщо розглядати величину , яку в зв’язку називають спектром сигналу, то такі величини для зсунутого та не зсунутого сигналу абсолютно однакові.

3. Теорема масштабу

, (1.13)

де – Фур’є образ не масштабованого сигналу, – масштабний коефіцієнт

Інший запис цієї теореми такий

, (1.14)

4. Похідна від сигналу, виражена через його Фур’є образ

, (1.15)

1.2. Згортка. Розмиття сигналу

Під згорткою двох функцій і розуміємо вираз:

. (1.16)

В теорії Фур’є перетворення зформульована, так звана теорема згортки, яка має вигляд:

. (1.17)

Суть цих співвідношень полягає в наступному. Наприклад, перший вираз читається таким чином – Фур’є образ від добутку двох функцій дорівнює згортці двох Фур’є образів.

Наведемо ще одне важливе співвідношення

. (1.18)

Нагадаємо геометричний зміст згортки дійсних функцій. Суть його дуже просто зрозуміти з рисунка 1.4. Фактично згортка є площею взаємного перекриття функцій і . На рис. 1.4, б зображена згортка прямокутного імпульсу шириною .

Як бачимо, ширина згортки вдвічі більше, ніж ширина самого імпульсу. Це загальний наслідок.

З цього факту випливає не менш важливий наслідок. Найменший за розмірами структурний елемент згортки має ширину більшу ніж ширина найменшого елементу функцій, які згортаються. Іншою мовою сигнал згорнутий з деякою функцією (наприклад, прямокутним імпульсом шириною a) розмивається і втрачає дрібну структуру. При цьому найменший за розмірами елемент перетвореного сигналу стає не вужче ніж подвійна ширина функції .

а б

Рис. 1.4

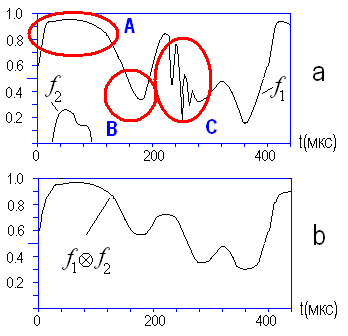
Рис. 1.5.

Цей факт ілюструється рисунком 1.5. Як бачимо дрібна структура сигналу зникає (регіон С рисунку а). Змінюється, але зберігається структура функції в регіоні типу В, де поперечні розміри елементів порядку ширини функції і лише в регіонах типу А структура перетвореного сигналу залишається практично такою самою як і в сигналі .

Відзначимо те, що лише згортання сигналу з нескінченно вузькою функцією ( -функцією) не приводить до зміни сигналу (див. співвідношення 1.18)

Повернемося до гармонійних сигналів, з різними частотами. При цьому будемо вважати, що вони однакової амплітуди та існують на протязі певного проміжку часу .

Спектри таких сигналів (лише додатні частоти) представлені на рисунку 1.6. Нижній рисунок збільшена за масштабом копія верхнього рисунку.

Як бачимо, кожному сигналу відповідає сплеск, позиція якого визначається його частотою. Ширина сплеску залежить від тривалості сигналу . Чим більше , тим вужче ширина сплеску. Природно, що величина сплеску залежить від амплітуди сигналу.

Тепер розглянемо спектр суми цих сигналів, заданих у відповідності до співвідношення 1.2, та зображеної на рисунку 1.1.

Природно, що в наслідок лінійності Фур’є перетворення в частотній області будуть також спостерігатися чотири сплески, у місцях які відповідають кожній частоті і картина спектру сигналу практично така сама як і в попередньому випадку.

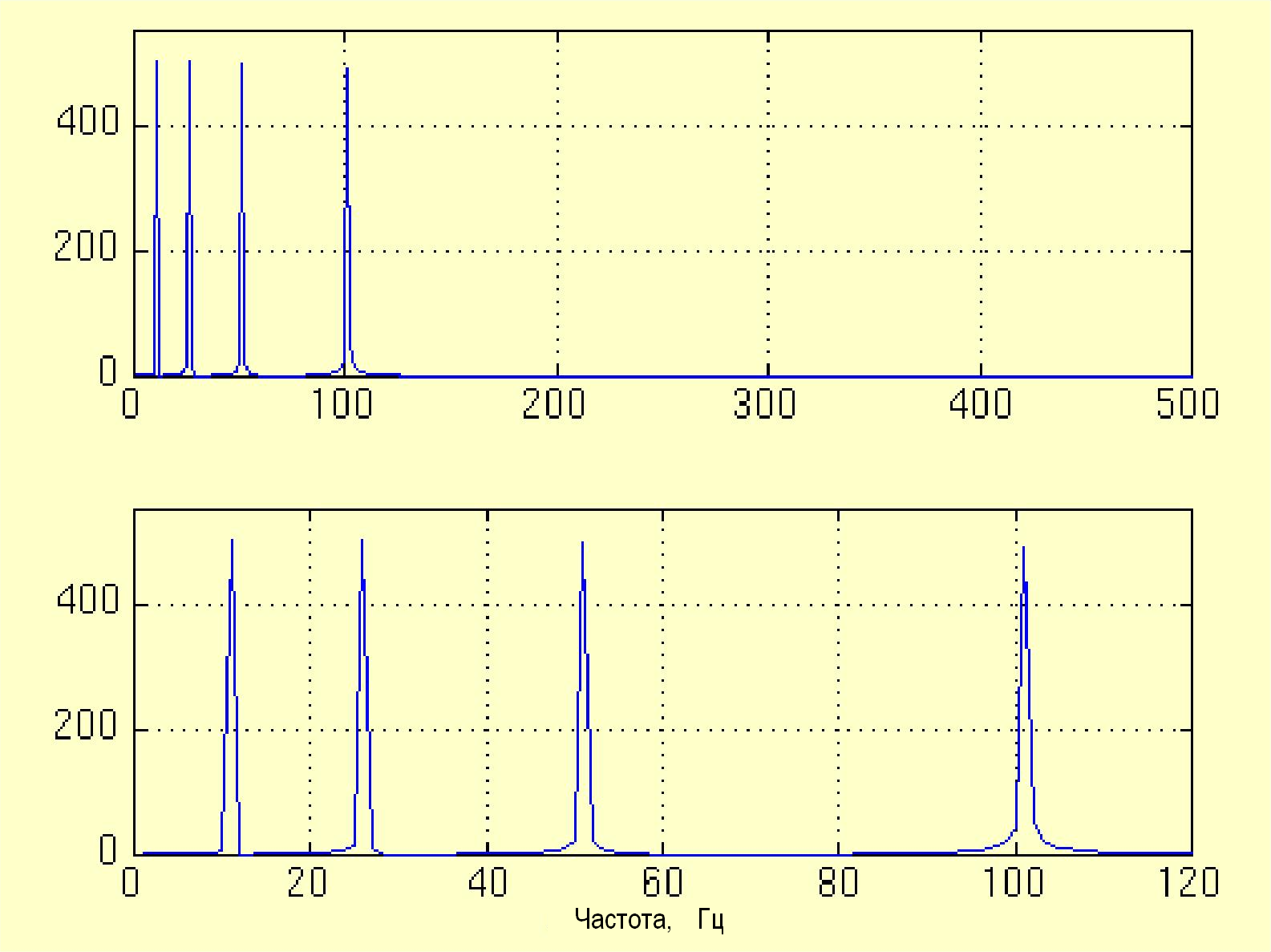
Рис. 1.7

Такі сплески досить просто ідентифікуються як за величиною так і за розташуванням. Як наслідок можна зробити однозначний висновок про внесок кожної гармонійної складової в початковий сигнал. Більш того іноді просто немає альтернативи спектральному аналізу сигналу. Наприклад, відомо, що так звані імітатори можуть досить точно «підробляти» мову, яка належить іншій людині. Якщо кваліфікація імітатора висока, то дуже часто відрізнити кому належить той чи інший фрагмент звукового повідомлення не можливо. В той же час спектри цих звукових повідомлень розрізняються кардинально.

Ще раз відзначимо, що, на відміну від рисунку 1.3. в частотній області сплески, які відповідають різним за частотою складовим сигналу внаслідок лінійності Фур’є перетворення та обмеженості часу його існування будуть зображатися не нескінченно вузькими сплесками однакової інтенсивності а подібно до того, як зображено на рисунку.

Таке розширення сплесків виникає в результаті того, що виконується перше співвідношення виразу (1.17) та того факту, що операція згортки приводить до згладжування та розширення сигналу.

Дійсно, нехай Фур’є образ сигналу . Тоді Фур’є образ обмеженого в часі сигналу (при довжині інтервалу ) може бути представлений у вигляді

. (1.19)

Згідно з 1.17 маємо

, (1.20)

де

З 1.20 випливає, що чим більше тим більше образ обмеженого в часі сигналу наближається до , оскільки наближається до -функції. І навпаки чим менше проміжок часу, коли існує сигнал тим більше згладжується . На решті, коли інтервал часу стає дуже малим тобто , вироджується у функцію з постійною амплітудою, оскільки Фур’є образ від -функції є одиницею. Іншими словами втрачається абсолютно вся інформація про сигнал.

Тепер розглянемо два випадки:

1. Сигнал є сумою чотирьох сигналів (5, 10, 25 та 50 Гц), які передаються одночасно (рисунок 1.8а) на протязі інтервалу часу , починаючи з моменту часу :

, (1.21)

Спектр цього сигналу наданий на рисунку 18б.

2. Гармонійні сигнали тієї самої частоти але кожний з них передається у свій проміжок часу

, (1.22)

Такий сигнал може бути подібним до зображеного на рисунку 1.9а. Спектр цього сигналу наданий на рисунку 19б.

Як бачимо з рисунків 1.18 та 1.19 і в першому і в другому випадку в точках частотної осі 5, 10, 25 та 50 Гц спостерігаються відповідні максимуми. Інакше кажучи характерні ознаки спектрів двох різних сигналів однакові. Більш того, якщо час на протязі якого існує кожний гармонійний сигнал з різними частотами такий самий як у попередньому випадку то внаслідок того, що для Фур’є перетворення виконується теорема зсуву та це перетворення лінійне, можна стверджувати ширина та інтенсивність сплесків така сама.

Інакше кажучи спектри сигналів, які взяті нами для прикладу і складаються з чотирьох гармонійних практично однакові незалежно від розташування їх гармонійних складових відносно осі часу.

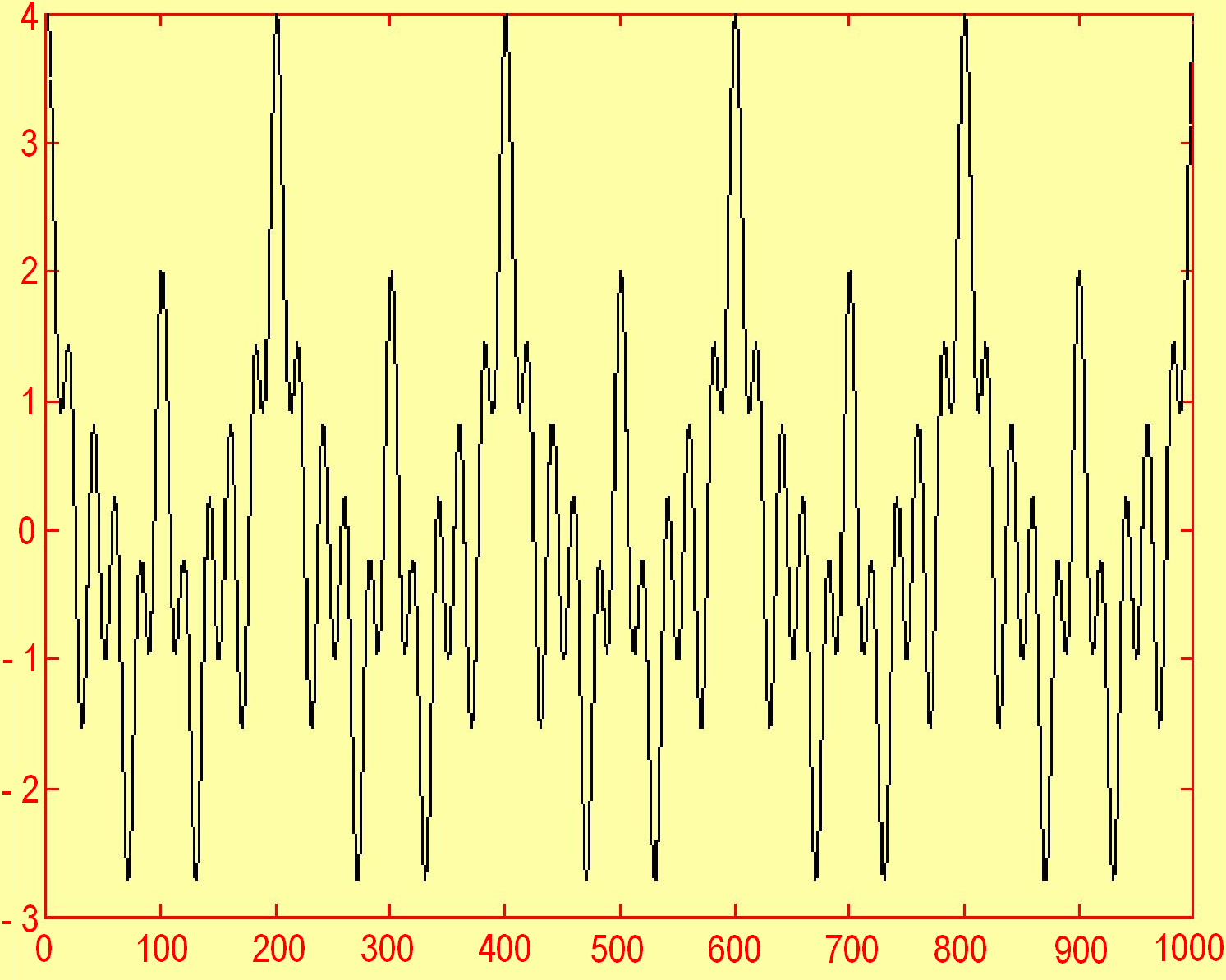
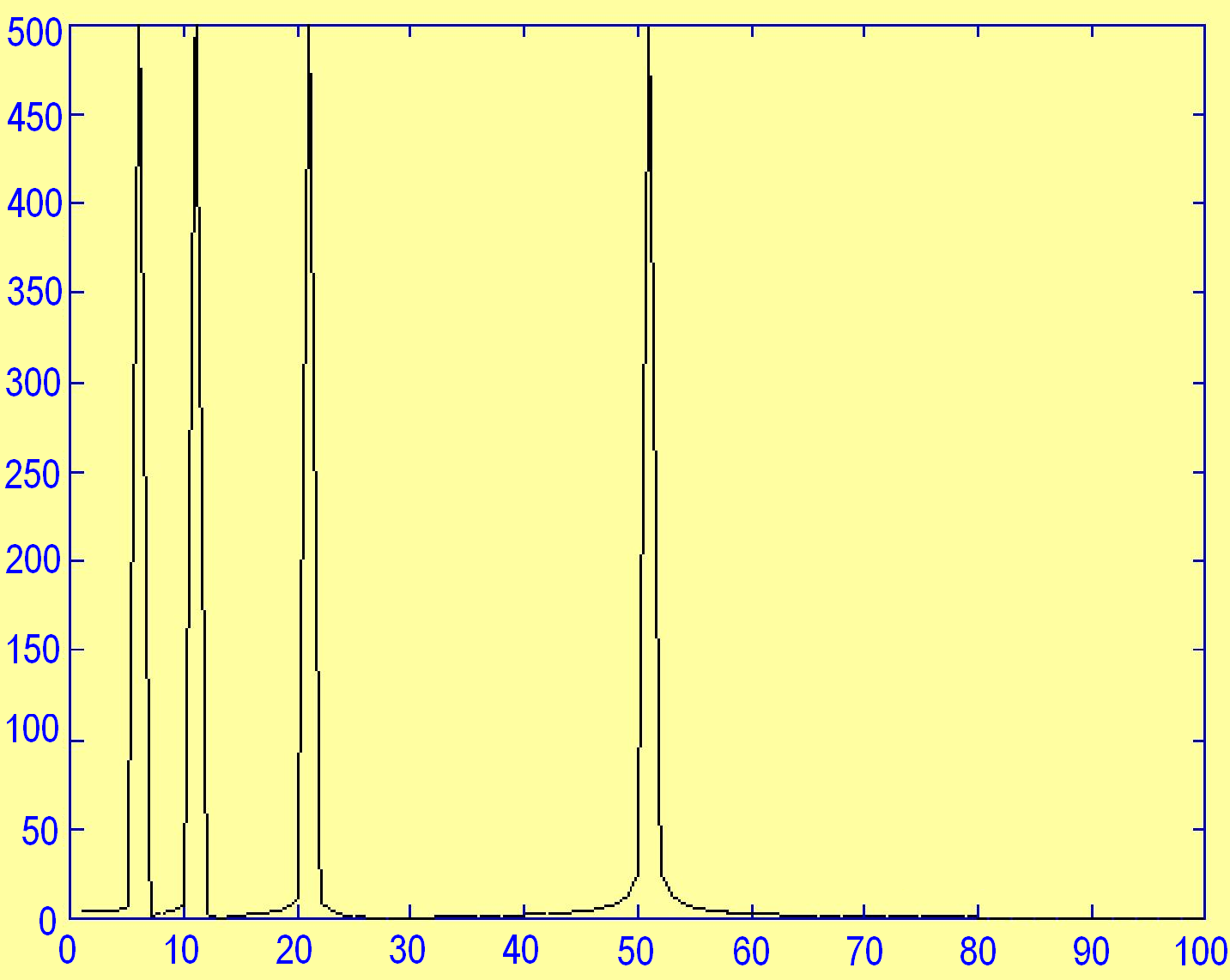
а б

Рис. 1.8

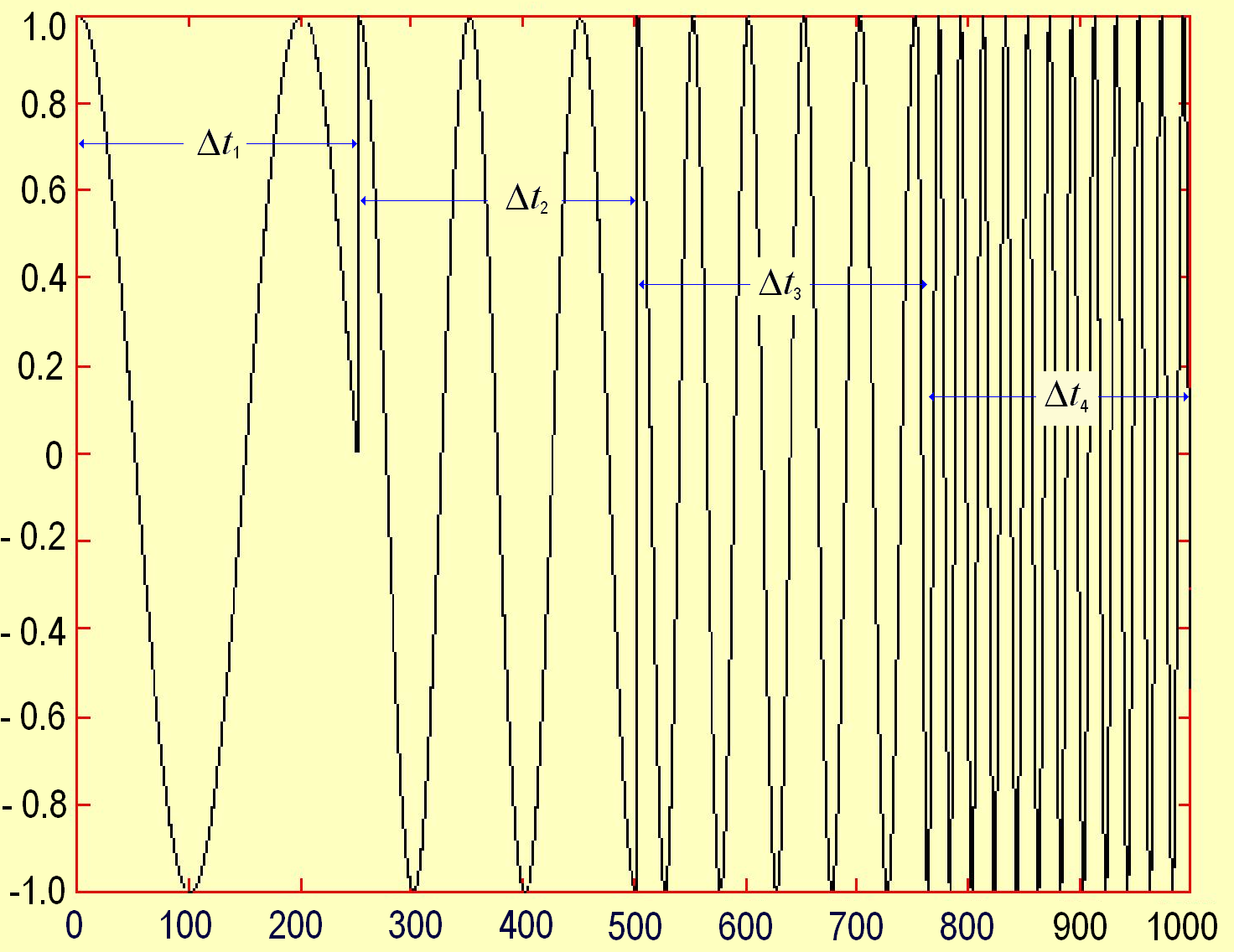
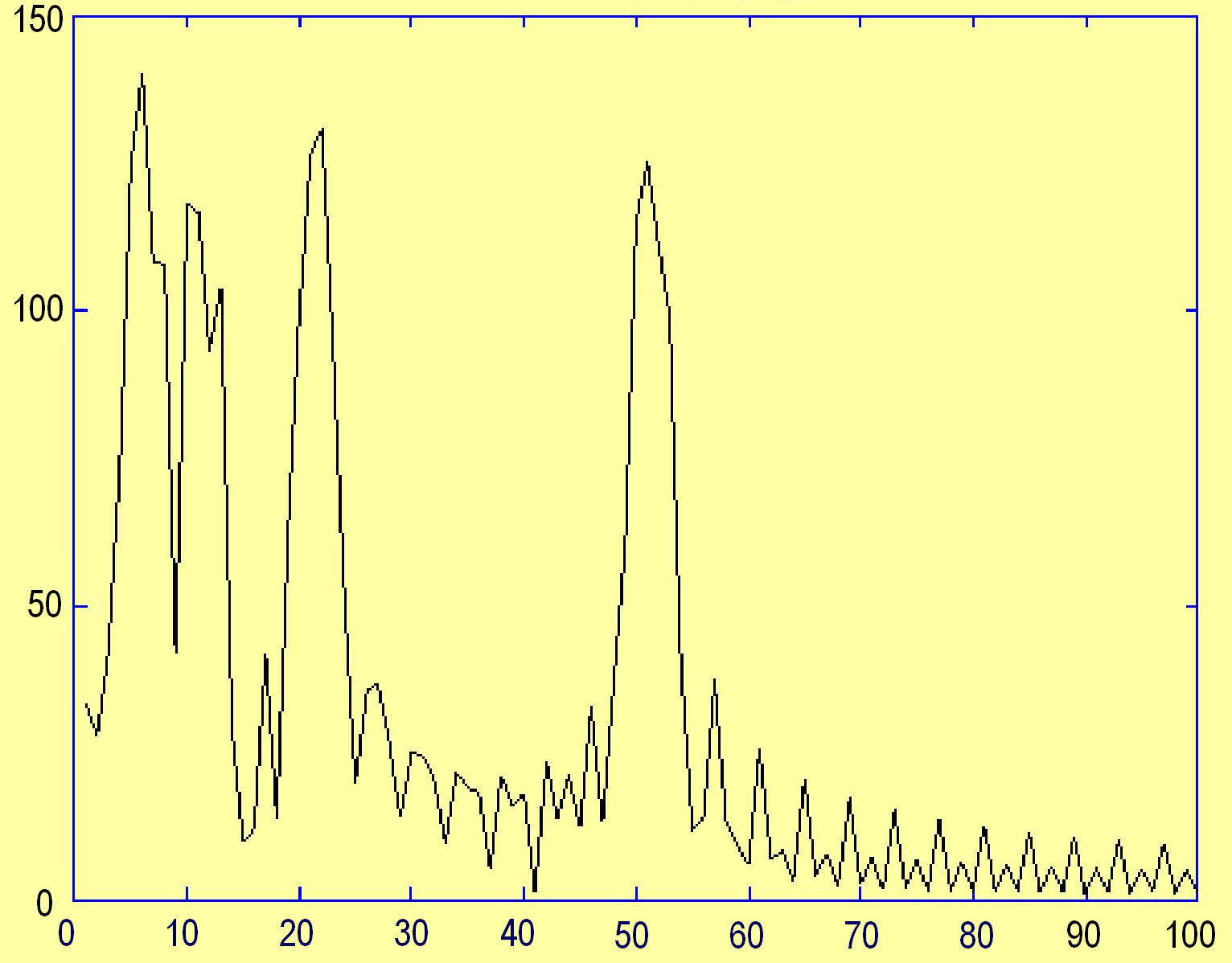
а б

Рис. 1.9

Чим реально відрізняються ці два сигнали? Відповідь проста. Перший з них – стаціонарний, тобто сигнал, характеристики якого не змінюються в часі. Другий не задовольняє цьому критерію. В перший період часу передається сигнал з мінімальною частотою, яка потім змінюється на середню і далі на високу.

Яка причина того, що два спектри дуже схожі? Відповідь така. При Фур’є перетворенні сигналу відбувається зміна представлення сигналу – перехід від амплітудно-часового до амплітудно-частотного представлення. Інакше кажучи за рахунок інтегрування по і безмежним границям інтеграла у виразі 1.3. відбувається повна втрата інформації про часову поведінку сигналу.

Звідси випливає висновок – очевидно, що Фур’є перетворення може бути ефективно застосовано насамперед до стаціонарних сигналів. Для аналізу не стаціонарних сигналів повинно існувати інше перетворення, яке не втрачає інформацію про зміну сигналу в часі.