5.3 Проекционное преобразование

В OpenGL поддерживаются ортографическая (параллельная) и перспективная проекция. При ортографической проекции видимый объем пространства имеет форму параллелепипеда, при перспективной – усеченной пирамиды.

Ортографическая проекция задается одной из функций:

void glOrtho( GLdouble left, GLdouble right, GLdouble bottom,

GLdouble top, GLdouble near, GLdouble far )

void gluOrtho2D( GLdouble left, GLdouble right,

GLdouble bottom, GLdouble top)

Параллелепипед видимого объема ограничен плоскостями отсечения, которые параллельны осям левосторонней системы координат и задаются расстояниями left, bottom и т.д. Функция gluOrtho2D() по умолчанию устанавливает расстояния до ближней и дальней плоскостей отсечения: near=-1 и far=1.

Для задания перспективной проекции служит функция:

void gluPerspective( GLdouble fovy, GLdouble aspect,

GLdouble near, GLdouble far )

Эта функция задает видимый объем в форме усеченной пирамиды в левосторонней системе координат (рис. 1.4). Угол поля зрения (по оси у) fovy лежит в диапазоне от 0 до 180 градусов. Угол видимости по оси x задается параметром aspect (обычно он вычисляется как отношение сторон экранного окна вывода). Параметры far и near задают расстояние от наблюдателя до плоскостей отсечения по глубине и должны быть положительными. Чем больше отношение far/near, тем хуже в буфере глубины будут различаться расположенные рядом поверхности, так как по умолчанию в него записываются значения глубины, нормированные в диапазоне от 0 до 1.

Рис. 1.4. Видимый объем, устанавливаемый с помощью функции gluPerspective().

Для задания перспективной проекции есть еще одна функция, с несколько другим набором параметров (рис 5):

void glFrustum( GLdouble left, GLdouble right, GLdouble bottom,

GLdouble top, GLdouble near, GLdouble far)

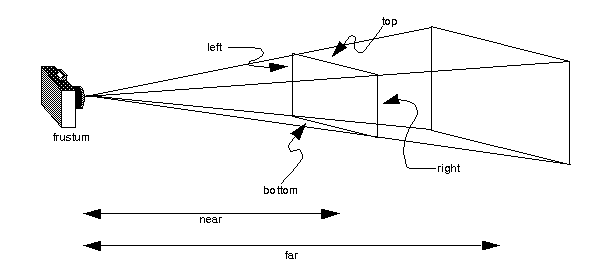
Рис. 1.5. Видимый объем, устанавливаемый с помощью функции glFrustum().

5.4 Оконное преобразование

После применения проекционной матрицы на вход следующего преобразования (перспективного деления, рис. 1.2) поступают так называемые усеченные (clipped) координаты вершин, расположенных внутри видимого объема. Значения всех компонент усеченных координат (x_c, y_c, z_c, w_c) находятся в диапазоне [-1,1]. Трехмерные нормированные координаты вершин вычисляются по формуле:

(x_n, y_n, z_n) = (x_c/w_c, y_c/w_c, z_c/w_c)

Полученные нормированные координаты подвергаются оконному преобразованию. Согласно аналогии с фотоаппаратом (рис. 1.2), оконное преобразование соответствует этапу, на котором выбираются размеры получаемого двумерного изображения. Размер изображения на экране – область вывода – является прямоугольником, заданным в оконной системе координат (рис. 1.6) с помощью функции:

void glViewPort( GLint x, GLint y, GLint width, GLint height )

Значения всех параметров задаются в пикселах и определяют ширину и высоту области вывода с координатами левого нижнего угла (x, y). Размеры оконной системы координат зависят от текущих размеров окна приложения, а точка-начало координат (0, 0) располагается в левом нижнем углу окна.

Рис. 1.6. Вершины, лежащие внутри видимого объема, проектируются на его переднюю стенку (ту, которая ближе к наблюдателю) и затем отображаются в области вывода на экране.

Вычислим оконные координаты центра области вывода (c_x, c_y):

c_x=x+width/2, c_y=y+height/2.

Введем обозначения p_x=width, p_y=height. Оконные координаты каждой вершины вычисляются по формулам:

(x_win, y_win, z_win) = ( (p_x/2) x_n + c_x , (p_y/2) y_n + c_{y ,} [(f-n)/2] z_n+(n+f)/2 )

Целые положительные величины n и f ограничивают минимальную и максимальную глубину точек, которые могут попасть в область вывода (по умолчанию n=0 и f=1). Глубина каждой точки z_win записывается в специальный буфер глубины (z-буфер), с помощью которого OpenGL удаляет невидимые линии и поверхности. Установить собственные значения n и f можно вызовом функции

void glDepthRange( GLclampd n, GLclampd f )

Если у нескольких вершин совпадают двумерные координаты (x_win, y_win), то в область вывода попадет вершина с минимальным значением глубины z_win.

В консольных приложениях функция glViewPort() обычно вызывается из функции, зарегистрированной с помощью функции макета glutReshapeFunc() в качестве функции-обработчика события изменения окна приложения.