2. Основы газодинамики сжимаемой жидкости

2.1 Уравнения равновесия и движения жидкостей

Жидкость, как сплошная среда, отличается от твердого тела легкой подвижностью своих частиц. В механике сплошной средой называют физические объекты, основные характеристики кото­рых (плотность, давление, температура и др.) изменяются не­прерывно. Движения жидкостей и газов имеют много общих свойств, поэтому их обычно изучают вместе.

В зависимости от основных свойств — сжимаемости и вязкости — жидкости соответственно разделяют на несжимаемые и сжимаемые и идеальные (невязкие) и реальные (вязкие).

Сжимаемость — это свойство вещества сопротивляться изменению своего объема. Если плотность среды при изменении давления и температуры не изменяется, такую среду называют несжимаемой. Плотность капельной жидкости (например, воды) при изменении давления практически не изменяется. Вообще оценку сжимаемости производят по числу Маха (М). Отношение скорости течения газа с в данной точке к местной скорости зву­ка а называют числом М или числом Маха:

М = с/а. (2.1)

Скорость звука в газе определяется его температурой и фи­зическими свойствами:

, (2.2)

где р — давление, v — удельный объем и Т — температура (К) газа в данной точке; R — универсальная газовая постоянная; k — показатель адиабаты.

В зависимости от числа М различают дозвуковые (М<1), звуковые (М=1) и сверхзвуковые (М>1) течения газов.

Число М является критерием сжимаемости. Действительно, предполагая в одномерном стационарном адиабатном потоке идеального газа изоэнтропное торможение, можно получить, на­пример, для дозвукового течения (М<1) приближенные форму­лы, показывающие зависимость отношения плотностей газа от числа М:

. (2.3)

Для разности давлений газа в этом случае

. (2.4)

Так как в несжимаемой жидкости ρ=const=ρ₀, делают тем меньшую ошибку, чем меньше число М. Например, воду нельзя рассматривать как несжимаемую жидкость при скорости более 400 м/с (такая скорость на практике не наблюдается), если ошибка в определении плотности не превосходит 3%. Воздух при скорости 100 м/с можно также считать несжимаемым, если погрешность в определении плотности не превосходит 4%.

Под жидкостью обычно понимают капельную жидкость, газ или пар. Следовательно, газ можно рассматривать как частный случай жидкости.

Для изменения формы твердого тела к нему необходимо приложить силы конечного, иногда довольно большого значения. Для медленной деформации жидкости достаточны самые ничтожные силы, которые в предельном случае бесконечно малой деформации равны нулю. Однако жидкость, подобно твердому телу, при быстрой деформации оказывает ей сопротивление. Но как только движение жидкости прекращается, это сопротивление очень быстро исчезает. Свойство жидкости оказывать сопротивление деформации называют вязкостью. При деформации вязкость проявляется в виде внутреннего трения.

Если в движущемся газе отсутствует внутреннее трение, такой газ называют идеальным. Реальные газы вследствие вязкости не могут скользить вдоль поверхности тела, так как скорости частиц, граничащих (соприкасающихся) с ней, равны нулю. Газ как бы «прилипает» к поверхности тела. Однако эта скорость резко возрастает при удалении от обтекаемой поверхности. На внешней границе весьма тонкого по сравнению с размерами тела пограничного слоя скорости газа достигают значений, соответствующих значениям свободного скольжения идеального газа. Поэтому понятие идеального газа может быть применено при расчете обтекания таких тел, как крыло, лопатки турбины, и др. В случае если пограничный слой отрывается от поверхности тела, характер течения вязкого газа значительно отличается от характера течения идеального газа.

При расчете паровых турбин непрерывное течение газа (перегретого пара) можно рассматривать как равновесный процесс. Это означает, что движущийся пар находится в термодинамиче­ском равновесии и имеет вполне определенные значения параметров (t и р, h и s и т. д.), непрерывно изменяющиеся с течени­ем времени и при переходе от одной точки потока к другой. Движение идеального газа при большинстве расчетов считают стационарным (установившимся). Таким образом, в каждой точке потока газа скорости с, а также другие параметры (р, v, t и т. д.) имеют определенные, не изменяющиеся во времени значения. Как правило, течение считают одномерным, т. е. изменения параметров и скорости газа происходят в одном направлении, а в остальных они либо постоянны, либо принимаются равным осредненным значениям.

Для расчета течения жидкости используют пять законов, выражающихся следующими уравнениями: сохранения массы (уравнение неразрывности); сохранения энергии (первый основной закон термодинамики); сохранения количества движения (закон импульсов); термическое уравнение состояния; калорическое уравнение состояния. Двумя последними уравнениями выражается второй основной закон термодинамики. Канал, в котором поток плавно ускоряется, называют соплом. Рассмотрим состояние газа в сечениях 1—1 и 2—2 сопла

(рис. 2.1) и запишем перечислен­ные уравнения.

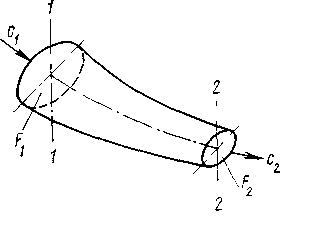
Рис. 2.1 Схема течения газа через сопло произвольной формы

Уравнение неразрывности. Это уравнение выражает закон сохранения массы для движу­щейся среды. Выделим в сопле два сечения 1—1 и 2—2 с площадями F₁ и F₂, перпендикулярными направлению движения потока. Массовым расходом D газа на­зывают массу вещества m, кото­рая протекает через поперечное сечение сопла в единицу време­ни τ, т. е. D = m/τ. При устано­вившемся течении массовый расход D через любое сечение ка­нала будет неизменным:

. (2.5)

Объемный расход газа через первое сечение сопла

_, (2.6)

где c₁ — скорость потока газа.

Объемный расход газа определяется как

V₁ =D₁*v₁ , (2.7)

где v₁ — его удельный объем.

П

(2.8)

риравнивая уравнения (28) и (27), получим

или .

Д

(2.9)

ля второго сечения соотношения будут аналогичны:

D₂v₂=F₂c₂ или D₂=(F₂c₂)v₂.

Т

(2.10)

ак какD₁=D₂=D, получим

D=(F₁c₁)v₁=(F₂c₂)/v₂=(cF)/v= ρcF=const,

где ρ =1/ v – плотность газа.

Т

(2.11)

огда для любого сечения

Dv=Fc.

Уравнение сохранения энергии. Запишем первый основной закон термодинамики (закон сохранения и превращения энергии) для потока 1 кг газа, протекающего от сечения 1—1 до сечения 2—2 сопла:

, (2.12)

где q — теплота, подведенная к потоку; — разность энтальпий,— разность кинетических энергий и _g(z2-z1) —разность потенциальных энергий в сечениях 1—1 и 2—2; l — работа, совершаемая газом на этом участке.

Если пренебречь изменением потенциальной энергии g(z₂-z₁), так как она мала, то уравнение (2.12) примет вид

q=h₂-h₁+(c₂²-c₁²)/2+l (2.13)

или

h₁+c₁²/2+q=h₂+c₂²/2+l. (2.14)

Соотношение (2.14), являющееся уравнением сохранения энер­гии для установившегося движения газа, справедливо независи­мо от того, сопровождается ли течение газа в системе потерями или происходит без потерь.

Если газ протекает через сопло при отсутствии теплообмена с внешней средой (q=0) и подвода или отвода механической энергии (l = 0), уравнение (2.14) принимает вид

(c₂²-c₁²)/2=h₁-h₂. (2.15)

Таким образом, при отсутствии обмена теплотой и механиче­ской энергией с внешней средой изменение кинетической энергии определяется разностью энтальпий, или теплоперепадом, между рассматриваемыми сечениями.

Уравнение количества движения. Будем исходить из основно­го закона динамики: ускорение прямо пропорционально силе и обратно пропорционально массе: a=F/m (второй закон Нью­тона). Количеством движения (или импульсом) называется ве­личина, равная произведению массы тела на скорость: Fτ=p=mc. Как и скорость импульс — величина векторная, используя понятие импульса, можно сформулировать основной закон динамики так: сила равна изменению импульса в единицу вре­мени, т. е.

(2.16)

Для замкнутых систем тел справедлив закон сохранения им­пульса, который можно сформулировать так: суммарный им­пульс замкнутой системы сохраняется при любых процессах, происходящих в ней.

Второй и третий законы Ньютона позволяют решить по су­ществу любую задачу механики. Правда, в некоторых случаях применение этих законов может быть связано с большими трудностями.

При установившемся движении импульс некоторой массы га­за в данном сечении остается постоянным. При переходе в дру­гое сечение импульс изменяется вследствие действия сил давле­ния и вязкости, внешних сил и др. При отсутствии обмена теп­лотой и механической энергией с внешней средой, а также вяз­кости, получим уравнение импульса, учитывающее только силы давления:

(2.17)

где R₁=p₁F₁ и R₂=p₂F₂ cилы давления в сечениях 1-1 и 2-2; m/τ=D – секундный расход газа.

Используя выражение D=Fc/v= ρcF, получим

(2.18)

(2.19)

или

Формулу (2.17) называют уравнением импульсов для потока идеального сжимаемого газа (без учета внешних воздействий и сил тяжести).

Если кроме сил давления необходимо также учитывать дру­гие силы, то в уравнении (2.17) под разностью сил R₁—R₂ пони­мают равнодействующую всех сил в проекции на направление движения.

Термическое уравнение состояния. Это уравнение связывает основные параметры состояния газа: давление р, температуру Т и удельный объем v. Для идеального газа

pv=RT или p =ρRT, (2.20)

где R— универсальная газовая постоянная.

Уравнение (2.20) легко получают из законов Бойля — Мариотта и Гей-Люссака.

Калорическое уравнение состояния. Под калорическими свой­ствами понимают внутреннюю энергию u, энтальпию h, изобар­ную C_p и изохорную C_v теплоемкости. Согласно уравнению Мен­делеева — Клапейрона, энтальпия

. (2.21)

По уравнению Майера

С_p = С_v + R (2.22)

можно определить универсальную газовую постоянную

. (2.23)

Отношение называют показателем адиабаты k. Показатель адиабаты перегретого водяного пара изменяется в преде­лах от 1,26 до 1,33, а для сухого насыщенного пара составляет 1,135.

Иногда калорическое уравнение состояния для реального га­за записывают в виде зависимости энтальпии от давления и тем­пературы. Для адиабатного процесса калорическое уравнение состояния имеет вид

(2.24)

(2.25)

или

.

Таким образом, решив систему уравнений (2.10), (2.15), (2.19), (2.21) и (2.25), которая является математической формулировкой общих законов течения газа,

(2.26)

можно найти его параметры в любом сечении сопла. Так, если известны параметры газа в сечении 1—1, показатель адиабаты k и площади F₁ и F_2, можно, решив систему уравнений (2.26), оп­ределить пять неизвестных параметров в сече­нии 2—2.